РДТТ конструкции технологии материалы 2020

timochka>> Зависит от связующего! ....
Mihail66> Ни надо ничего про связующее. Давай будем считать что количество связки для обоих случаев одинаковое.

Еще зависит от того как связующее разрушается: хрупко, пластично, линейно или нет. Без учета связующего никак.

timochka>> Для армирования 0, 90 оптимальные толщины слоев должны быть 1 : 2. Суммарно 3.
timochka>> Для армирования 90, -45, +45 оптимальные толщины должны быть 1 : 1.41 : 1.41, суммарно 3.8.
Mihail66> А это еще откуда?

Да это то просто. Армирующие нити намного жестче связующего. Т.е. при одинаковых деформациях основную долю нагрузки несут волокна. А связка нагружена намного меньше. В этом и есть бонус композитов. Для упрощенного расчета выкидываем связку, оставляем только нитки. Они работают только на растяжение. Нагрузка известна: 1*q вдоль, и 2*q по касательной. Считаем нагрузку в нитках и прикидываем насколько какие нитки сильнее нагружаются. Соответвенно наращиваем толщину слоя пропорционально нагрузке.

Mihail66> Давай-ка мы будем оперировать слоями одинаковой толщины.
Тогда какие-то слои будут избыточно прочными.

Mihail66> Т.е. для первого варианта это 3 слоя ровинга определенной ширины и толщины, уложенные вплотную без зазоров. И для второго варианта все точно так же, только углы ориентации отличаются.
Mihail66> Итак - 1. армирование по схеме 0/90/0 (3 слоя),
Наоборот 90/0/90. 2 слоя намотки по кольцу, и один вдоль баллона. Углы идут от Оси X.

Mihail66> 2. армирование по схеме +45/-45/0 (3 слоя). И задаемся условием, что в обоих вариантах одинаковое количество связки, они имеют одинаковую толщину, и у них одинаковая масса.

Опять таки +45/-45/90. Слоя вдоль баллона нет, иначе совсем не оптимально.

И давай для простоты возмем, что масса связки пропорциональна толщине стоя (количеству ниток армирования). Т.е. пропитка или препрег одинаковые во всех слоях. Так оно вернее будет.

Если все слои одинаковой толщины, а вторая схема требует разной толщины для оптимума, то выходит избыточная прочность по направлению вокруг. И мы вместо оптимального 1.41 : 1.41 : 1 делаем 1.41 : 1.41 : 1.41. Т.е. на 0.41 / (1.41 + 1.41 + 1) = 10,7% толще оптимума. И на 41% толще чем с первой схемой армирования, и тяжелее. Но и жестче.

Для второй схемы жесткость по оси Y будет Ey=2.41, а по оси X Ex = 1.
Значит при второй схеме деформации волокон (а значит и связки) вдоль оси Y будут на 2 / 2.41 = 83%, на 17% меньше. Это при линейном законе нагружения у связки. И напряжения в связке SigmaY будут на 17% меньше во втором случае. А по X - SigmaX, будут одинаковы в обоих случаях.
В результате мы попадаем в другую точку на кривой критерия прочности связки. И где эта точка будет находится зависит еще и от типа этой кривой. Т.е. типа связки.

Например, возьмем линейно нагружаемую связку которая разрушается хрупко - полностью отвержденная эпоксидная смола. Критерий прочности у нее сплошная линия на графике проведенная под -45 градусов (приведено 3 варианта a, b, c - смолы разной прочности). Пунктирные возрастающие линии соответствуют росту нагрузки при первой и второй схемам армирования.

Теперь для очень прочной смоле - линия ©. Связующее выдерживает нагрузку при любой схеме армирования. Значет берем то что потоньше и полегче - схему 1.
При смоле средней прочности - линия (b) связущее выдерживает нагрузку по схеме 2, но разрушается по схеме 1. Берем схему 2.
При совсем слабой смоле - линия (a), связка разрушится при любой схеме армирования. Нужно наращивать толщину. Волокна будут избыточно прочными. На схема 2 быстрее окажется под линией критерия прочности. Т.е. наращиваем толщину и берем схему 2.

В реальной жизни для рекордных давлений не бывает слишком прочной смолы. Поэтому схема 2 используется чаще. Но если давления умеренные, то схема 1 даст меньший вес.

PS Я на сегодня всё, поздно уже очень.

Mihail66> А чтобы тебе было понятно в чем здесь подвох, поясню. Существует мнение, что если главные векторы сил в этом баллоне расположены не вдоль ориентации волокон, то векторное сложение этих сил для таких анизотропных материалов не применимо, в чем некоторые из присутствующих на форуме сильно сомневаются.

1) Векторное сложение не применимо если главные направления тензора жесткости (зависит от схемы армирования) не совпадают с главными направлениями векторов нагрузок. Доказательство там от противного. Нагрузки и модуль упругости это всегда тензора. Ну и уравнение Гука соответсвенно в тензорной форме. Но в некоторых частных случаях тензора сворачиваются до скаляров главных компонент. Один из случаев это изотропия материала. Другой - совпадение главных осей в обоих тензорах.

2) Разложение нагрузок по осям при расчете деформаций неприменимо если закон нагружения материала нелинейный. Пример полиэтилен армированный нейлоном.

Те кто сомневаются могут учебник по теории упругости почитать. Но это так себе занятие, если не механик-прочнист по образованию. Материал 4-го курса.

timochka> Еще зависит от того как связующее разрушается: хрупко, пластично, линейно или нет. Без учета связующего никак.

Нам для сравнительной оценки это не важно.

Mihail66>> Давай-ка мы будем оперировать слоями одинаковой толщины.
timochka> Тогда какие-то слои будут избыточно прочными.

А если посчитать?

Mihail66>> Итак - 1. армирование по схеме 0/90/0 (3 слоя),
timochka> Наоборот 90/0/90. 2 слоя намотки по кольцу, и один вдоль баллона. Углы идут от Оси X.

Да, точно. Как ты говоришь это верно (мой косяк).

timochka> Опять таки +45/-45/90. Слоя вдоль баллона нет, иначе совсем не оптимально.

Так в этом вся соль.
Мы технологически не имеем возможности пустить слой ориентированный вдоль оси, нам сопло мешает.
А зачем он нам нужен? Два слоя под углом 45 будут иметь такую же прочность в продольном направлении, как один слой строго вдоль оси.

timochka> И давай для простоты возмем....

ОК! Масса связки пропорциональна количеству ниток.

timochka> Если все слои одинаковой толщины, а вторая схема требует разной толщины для оптимума, то выходит избыточная прочность по направлению вокруг.

Отчего же так? Мы ведь вместо одного слоя с углом 0 имеем два слоя с углом 45, таким образом напряжение в продольном направлении должно оставаться неизменным. А для кругового направления мы имеем всего один слой под 90 (вместо двух), а второй недостающий слой круговому слою достается опять же от двух слоев под 45.

timochka> Для второй схемы жесткость по оси Y будет Ey=2.41, а по оси X Ex = 1.

Почему так? Если считать по векторному сложению сил, то для Ey = Ex = 1.

timochka> Например, возьмем линейно нагружаемую связку которая разрушается хрупко - полностью отвержденная эпоксидная смола....

С твоими дальнейшими раскладами по связке я пока не разобрался. Изучаю.

timochka> 1) Векторное сложение не применимо если главные направления тензора жесткости (зависит от схемы армирования) не совпадают с главными направлениями векторов нагрузок.

Так значит это как раз относится ко второй схеме армирования (+45/-45/90)?

Mihail66> А чтобы тебе было понятно в чем здесь подвох, поясню.

"Подвох"

Mihail66> Существует мнение, что если главные векторы сил в этом баллоне расположены не вдоль ориентации волокон, то векторное сложение этих сил для таких анизотропных материалов не применимо, в чем некоторые из присутствующих на форуме сильно сомневаются.

Для сил применимо!
Для напряжений нет.
Потому, что сила - это вектор (последовательность по математике)
А напряжение - это тензор (матрица по математике)

Mikhal> У кого баллон получился лучше?

Об этом пока лучше не спрашивать

Mikhal> Чем этот баллон плох?

Да собственно тут нет соревнований "лучше/хуже". Вопрос в оптимизации - проще, дешевле, легче и крепче.

ПС. Я тут книжечку на аукционе покупаю, никак не куплю - "Оптимальное армирование оболочек вращения из композиционных материалов (1977)", как раз на нее ссылается Фархутдинов в своих заявлениях относительно прочности спиральной намотки. Может она прояснит, что там за потери прочности.

Mihail66> Вопрос в оптимизации - проще, дешевле, легче и крепче.

крепче/легче=лучше. про проще(дешевле) можно поспорить. У кого проще(дешевле) при ухудшении "лучшего".

Mihail66> Я тут книжечку на аукционе покупаю, никак не куплю - "Оптимальное армирование оболочек вращения из композиционных материалов (1977)"

Заказал у корифеев науки, выложу, если дадут. Там сплошная математика.

Mikhal> крепче/легче=лучше. про проще(дешевле) можно поспорить.

В этом случае выиграет баллон произведенный на предприятии который "Протоны" наматывает.
Вот поэтому вопрос именно в том, как сделать проще и дешевле без значительных потерь прочности.

Mikhal> Заказал у корифеев науки, выложу, если дадут. Там сплошная математика.

Давай! Похоже аукцион я не осилю, за эти непонятные 144 станицы сейчас 3 косаря просят.

Mihail66> Мы технологически не имеем возможности пустить слой ориентированный вдоль оси, нам сопло мешает.

Давай про сопло забудем пока. Там все сильно сложнее чем кажется. Все рассуждения пока про прочность центрального сегмента тонкого и очень длинного баллона. В районе днищ там такая веселуха начинается, что проще на компе посчитать.

Mihail66> А зачем он нам нужен? Два слоя под углом 45 будут иметь такую же прочность в продольном направлении, как один слой строго вдоль оси.

Конечно нет! И видимо в этом основа всего недопонимания в этом топике.
Дальнейшие рассуждения про равнопрочность некорректны именно из-за этого посыла.

timochka>> Для второй схемы жесткость по оси Y будет Ey=2.41, а по оси X Ex = 1.
Mihail66> Почему так? Если считать по векторному сложению сил, то для Ey = Ex = 1.

Жесткость армировки (на растяжение, и только на растяжение) пропорциональна толщине слоя. Т.е. кладем в 2 раза больше ниток, жесткость на растяжение получаем в 2 раза больше. И деформация в у него в 2 раза меньше. Это все из-за того, что единичное волокно теперь несет в 2 раза меньшую нагрузку.

timochka>> 1) Векторное сложение не применимо если главные направления тензора жесткости (зависит от схемы армирования) не совпадают с главными направлениями векторов нагрузок.
Mihail66> Так значит это как раз относится ко второй схеме армирования (+45/-45/90)?

Не так. Если я не накололся в расчетах, именно для этой схемы армирования главные оси тензора жесткости чудесным образом совпали.

Короче, я понял что надо еще одну часть делать по расчету усилий в волокнах и расчете жесткости. Это сегодня, но чуть погодя.

timochka> Конечно нет! И видимо в этом основа всего недопонимания в этом топике.

Именно так!

timochka> Жесткость армировки (на растяжение, и только на растяжение) пропорциональна толщине слоя.

Не так! Мы ведь условились что толщина слоя у нас неизменная. А вот при разных углах (0, 90, или 45) количество нагруженных ниток в этих слоях будет меняться.

Проще разобрать частный пример. Предположим -

Баллон диаметром 100мм, ширина нитки 1мм, прочность нитки 1кгс.
1. Укладываем вплотную по равнонагруженной схеме 90/0/90.
Тогда с углом 0 на окружность ляжет 314 ниток, и прочность вдоль оси будет 314кгс. По кольцу будем иметь 2 слоя, значит кольцевая прочность будет такой же.

2. А в схеме +45/90/-45 на окружность ляжет всего 314/1,41=222,7 ниток,
но слоев будет уже два 222,7*2=445,4 нитки.
А т.к. нитки будут уложены под углом, то прочность вдоль оси будет 445,4*0,707=314. Т.е. опять те же 314кгс что и для первого варианта. По кольцевой прочность для этих двух слоев будет в 2 раза меньше, но там начинает работать третий слой с углом 90. И таким образом баллон снова получается равнонагруженным.

Итог - оба баллона имеют по 3 слоя, и у них одинаковая прочность.

timochka> Т.е. кладем в 2 раза больше ниток, жесткость на растяжение получаем в 2 раза больше.

Вот как раз из-за того, что нитки укладываются под углом, их не становится в 2 раза больше.

Но этот пример строился именно на векторном сложении сил, и связка в нем не учитывалась. А вот как поведет себя связка, тут уже вопрос.

Mihail66>> Так значит это как раз относится ко второй схеме армирования (+45/-45/90)?
timochka> Не так. Если я не накололся в расчетах, именно для этой схемы армирования главные оси тензора жесткости чудесным образом совпали.

Ну тогда получается, что можно спроектировать множество различных схем армирования, лишь бы в целом баллон выходил равнонагруженным. И величина углов уже не будет иметь никакого значения, т.к. тензоры будут совпадать с главными силами.
К примеру схемы +54,7/-54,7 (2 слоя), 90/0/90 (3 слоя), +45/90/-45 (3 слоя), 90/+35,3/-35,3/90 (4 слоя), а для большего количества слоев этих схем можно навыдумывать прорву.

timochka> Короче, я понял что надо еще одну часть делать по расчету усилий в волокнах и расчете жесткости. Это сегодня, но чуть погодя.

Отлично! Может так и доберемся до правды. И останется разобраться с этой бодягой применительно к сферическим днищам.

Mihail66> Ну тогда получается, что можно спроектировать множество различных схем армирования, лишь бы в целом баллон выходил равнонагруженным. И величина углов уже не будет иметь никакого значения, т.к. тензоры будут совпадать с главными силами.

И получается, что надо мотать пару наклонных слоёв под таким углом, чтоб днища хорошо закрепились.
И с плотностью соответствующей осевой силе.
А потом доматывать по кругу, чтоб и поперечной силе соответствовать.

Остаётся только связку сделать достаточно эластичной, чтоб она первой не рвалась.

Mihail66>>> Так значит это как раз относится ко второй схеме армирования (+45/-45/90)?
timochka>> Не так. Если я не накололся в расчетах, именно для этой схемы армирования главные оси тензора жесткости чудесным образом совпали.
Mihail66> Ну тогда получается, что можно спроектировать множество различных схем армирования, лишь бы в целом баллон выходил равнонагруженным. И величина углов уже не будет иметь никакого значения, т.к. тензоры будут совпадать с главными силами.

Я сейчас застрелюсь от этого мракобесия.

1. Главных сил в цилиндрических оболочках только две вдоль оси и по кольцу и они обе существуют сами по себе и они обе плевать хотели друг на друга.
2. НИКОГДА НИКОГДА ПРИНИКОГДА эти две силы не будут направлены в цилиндре под каким-либо другим углом.
3. Научись понимать смысл написанного, в частности фразы "чудесным образом"!
4. Величина углов - это самая присамая значитальная зависимость в потери прочности для композита.
5. Тензон - это не вектор!
6. Тензор в вектор здесь вырождается только при допущениях вроде, что у нас связка в 100!!! раз слабее волокна на разрыв и тогда от тензора остаётся лишь главная диагональ главных нормальных напряжений и они при этом ОБЯЗАТЕЛЬНО ПРИОБЯЗАТЕЛЬНО ОБЯЗАНЫ СОВПАДАТЬ по углам направления с силами в цилиндрической оболочке. И это происходит только при углах 0° и 90°.
7. Под другими углами сила будет складываться векторно (любая диагональ больше любого из катетов в прямоугольном треугольнике => нагрузка растёт) для волокна, а напряжения нет (они вообще будут уменьшаться!), так как будут влиять касательные составляющие тензора ТАУ, которые отвечают за связку, адгезию и пр., так как под углом начинает всё больше работать связка, а не волокно, поэтому будут потери даже при соблюдении равнопрочности.
8. В больших промышленных РДТТ цилиндрическая часть корпуса короткая = оболочка сфера и им плевать на оптимизацию цилиндра! поэтому у них ±45/90.

Xan> И получается, что надо мотать пару наклонных слоёв под таким углом, чтоб днища хорошо закрепились.
Xan> И с плотностью соответствующей осевой силе.

Для днищ вроде бы прописано условие, что они и цил.часть будут в любом случае одинаково нагружены по продольной силе, если угол на них будет в диапазоне от 0 до 54,7 и огибание будет идти по геодезической. При угле более 54,7 донца уже не будут удерживаться, т.к. вектор силы пойдет по касательной к сферической поверхности.

Xan> А потом доматывать по кругу, чтоб и поперечной силе соответствовать.

А вот тут начинается проблема. Домотать по кругу мы можем только на цилиндрической поверхности, а та часть сферы которая расположена на участке от 54,7* и до 90* так и останется тонкой. В то время как участок от 0* и до 54,7* наоборот будет иметь излишнюю толщину и прочность. И поэтому в сферических частях баллона нужно делать жесткие вставки на которую ляжет композит. Или делать многозонные композитные донца, где толщина стенок будет изменяться ступенчато. Но такая конструкция применима только для очень многослойных баллонов, а у нас в кухонном РДТТ-строении используется как правило не более 2-3 слоев.

Xan> Остаётся только связку сделать достаточно эластичной, чтоб она первой не рвалась.

Ага! Эта тема уже торчит в могзу. Уже достали из кладовки смолу 3Д-Меджик, но она падла испортилась. Но вот тут-то как раз возможно, что компаунд на Этале будет лучше чем на ПЭПА, т.к. для Этала удлинение разрыва больше.

Mihail66>> А зачем он нам нужен? Два слоя под углом 45 будут иметь такую же прочность в продольном направлении, как один слой строго вдоль оси.
timochka> Конечно нет! И видимо в этом основа всего недопонимания в этом топике.

Так, давайте начнем с того, что я наврал с расчетом усилий в волокнах для схемы армирования 90,-45,45. Лень было полный расчет писать, прикинул на коленке, и попал пальцем в небо. 20 лет этим не занимался, навык ушел.

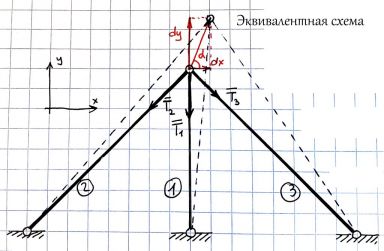
Поэтому давайте считать строго. Берем некую точку О на границе нашего элемента. К ней соответвенно сходятся 3 волокна из трех слоев. Как волокна приходят в нашу точку можно выбрать по разному, но мы возмем чтоб все волокна работали на растяжение, так удобнее (см. рисунок). Все волокна считаем одинаковыми.
Теперь мы немножко смещаем нашу точку O на расстояние (dx, dy) по соответвующим осям. Для простоты расчета примем dx < dy (в остальных местах результат возьмем по симметрии). Тогда в нашей эквивалентной схеме все волокна работают на растяжение.

Теперь запишем уравнения (см второй рисунок).
1) насколько удлинится каждое волокно при таком смещении точки О.
2) считая волокна работающими только на растяжение берем силу реакции Ti в i-м волокне. k - коэффициент упругости волокон (линейная деформация).
3) Нагрузка Q которая вызывает такое перемещение равна векторной сумме реакций всех волокон.
4) Закон Гука в матричной форме связывает вектор смещения точки О с вектором нагрузки Q. C - матрица жесткости системы.

Теперь нужно вычислить матрицу жесткости C и узнать как проходят ее главные вектора. Т.е. проверить совпадает ли направление вектора смещения с направлением вектора нагрузки.
Я проделал все вычисления и получил:
Qx = k * dx
Qy = 2k * dy

Ура! Для этой схемы армирования все совпало. Для других углов армирования может и не совпасть.
Из предыдущих частей мы знаем, что для нашего баллона Qy = 2 * Qx.
Т.е. получаем dx = dy при слоях одинаковой толщины.
Это означает, что наш кусочек стенки баллона S растянут одинаково по осям x, y.
Как при этом растянутся волокна каждого слоя уже понятно, удельные удлиннения будут одинаковые. А значит слои равнопрочные! А мои предыдущие прикидки про разную нагрузку в слоях просто не верны.

timochka>> Жесткость армировки (на растяжение, и только на растяжение) пропорциональна толщине слоя.
Mihail66> Не так! Мы ведь условились что толщина слоя у нас неизменная. А вот при разных углах

Погоди. Это в принципе всегда так для одного слоя. Но эти рассуждения сейчас не нежны, т.к. я нашел свою ошибку в разложении сил по волокнам. Посмотри исправленый полный расчет.

Mihail66> Но этот пример строился именно на векторном сложении сил, и связка в нем не учитывалась. А вот как поведет себя связка, тут уже вопрос.

Причем самый главный вопрос. Бывает, что волокна вполне держат, а связка рассыпается. Тогда приходится мотать больше волокон, чтоб уменьшить деформацию и снять нагрузку со связки.

Mihail66>>> Так значит это как раз относится ко второй схеме армирования (+45/-45/90)?
timochka>> Не так. Если я не накололся в расчетах, именно для этой схемы армирования главные оси тензора жесткости чудесным образом совпали.
Mihail66> Ну тогда получается, что можно спроектировать множество различных схем армирования, лишь бы в целом баллон выходил равнонагруженным. И величина углов уже не будет иметь никакого значения, т.к. тензоры будут совпадать с главными силами.

Они не для всех углов будут совпадать. Это просто для конкретно это схемы так удачно вышло. А возьми, например 90, 60, -30 - и все приплыли. Полный расчет только в тензорной форме и возможен.

Mihail66> И останется разобраться с этой бодягой применительно к сферическим днищам.
С днищами - извините ребята. Я 20 лет уже этим не занимался и нихрена не вспомню. А учебник курить это свободная неделя нужна, да где ее взять.
Помню только, что у днищ толщина нарастает из-за того, что все волокна сходятся туда. И все, оболочка не тонкая - пожалте бриться. Расчет толстой оболочки - это другой коленкор, там слои не равнонагруженные. Появляются изгибающие моменты, касательные напряжения, трехосевое напряженное состояние. Это лучше на машине считать.

SashaMaks> 1. Главных сил в цилиндрических оболочках только две вдоль оси и по кольцу и они обе существуют сами по себе и они обе плевать хотели друг на друга.
SashaMaks> 2. НИКОГДА НИКОГДА ПРИНИКОГДА эти две силы не будут направлены в цилиндре под каким-либо другим углом.

Я ругаться не буду. Только замечу, что это верно ТОЛЬКО для линейно деформирующихся связок и волокон. В аэроспейсе баллоны могут посчитать и так, что они работают за пределом линейного деформирования. Все равно один раз лететь, и циклический ресурс не нужен.
Но для стекловолокна, углеволокна, бороволокна на хрупкой связке (эпоксидка) это, конечно, верно.
В своем расчете я линейным допущением пользуюсь. Иначе все совсем печально получится.

SashaMaks> 8. В больших промышленных РДТТ цилиндрическая часть корпуса короткая = оболочка сфера и им плевать на оптимизацию цилиндра! поэтому у них ±45/90.

Как не удивительно, но по расчету вышло, что ±45/90 тоже оптимальное армирование эквивалентное 90/0/90 по прочности. Можешь проверить, конечно, т.к. ошибки возможны.

timochka> Причем самый главный вопрос. Бывает, что волокна вполне держат, а связка рассыпается. Тогда приходится мотать больше волокон, чтоб уменьшить деформацию и снять нагрузку со связки.

Именно! И как раз это я вижу экспериментально. Нитки еще не порвались, а баллон уже потек.
И вот мы добрались до самого главного. Как определить в какой схеме армирования наша хрупкая связка треснет быстрей? Опять же на примере двух любимых нами арматур - 90/0/90 и +45/-45/90.

timochka> Они не для всех углов будут совпадать. Это просто для конкретно это схемы так удачно вышло. А возьми, например 90, 60, -30 - и все приплыли. Полный расчет только в тензорной форме и возможен.

Ну так поэтому я "разнокосые арматуры" в принципе не рассматриваю. А что касается симметричных раскладок то с ними все должно выходить так же пушисто.

timochka>> Причем самый главный вопрос. Бывает, что волокна вполне держат, а связка рассыпается. Тогда приходится мотать больше волокон, чтоб уменьшить деформацию и снять нагрузку со связки.
Mihail66> Именно! И как раз это я вижу экспериментально. Нитки еще не порвались, а баллон уже потек.
Mihail66> И вот мы добрались до самого главного. Как определить в какой схеме армирования наша хрупкая связка треснет быстрей? Опять же на примере двух любимых нами арматур - 90/0/90 и +45/-45/90.

Ну смотри, у обоих схем матрица жесткости, или модуль упругости для сплошной среды одинаковая! Сложный случай я разобрал, а 90/0/90 ты и сам легко разберешь (или верь на слово).

1  0
0  2

Т.е. деформироваться они будут одинаково.
Если связка разрушается, то можно как Xan предлагал перейти на эластичную связку. Если возможно, конечно.
Но я бы рекомендовал домотать больше волокна и не искать себе приключений. Технология домашняя, стабильность низкая, плюс нагрев. Коэффициент запаса прочности меньше 2-х лучше не закладывать.

Расчет простой. Увеличивая толщину волокна в 2 раза, ты получаешь в 2 раза меньшие деформации. И в 2 раза меньшую нагрузку в связующем.

Mihail66> Ну так поэтому я "разнокосые арматуры" в принципе не рассматриваю. А что касается симметричных раскладок то с ними все должно выходить так же пушисто.

Не знаю! Я боюсь так сразу утверждать, что для всех симметричных раскладок все так совпадет. По памяти не скажу, это проверять надо.

timochka> Ну смотри, у обоих схем матрица жесткости, или модуль упругости для сплошной среды одинаковая! Сложный случай я разобрал, а 90/0/90 ты и сам легко разберешь (или верь на слово).
timochka> Т.е. деформироваться они будут одинаково.

Так в том то и дело, что все это я вижу, и именно поэтому прихожу в "неистовство" когда вдруг в авторитетных источниках вижу заявления о том, что (например) диагональная намотка будет иметь прочность на уровне 0,85-0,9 в сравнении с продольно поперечной.