-
/7213de79b2c4d639f0cf7961ee32d674.png)
Разбор ошибок Олейника (ligaspace) при расчете радиации в поясах Ван Аллена
Теги:
Благодаря одному трололо мне пришлось немного воткнуться в тему, и раз так случилось, то решил постить и сюда, чтоб не пропало. Возможно, со временем напишу подробный разбор этого выброса калечного сознания, пока первая порция:
Вот сравнение доз радиации при пролете через протонный пояс предоставленных Олейником и пересчитанных мною по его «данным» и «формуле». Как видно, у меня воспроизвелись его цифры, что значит что я верно понял как он их получил:
Теперь рассмотрим эту самую «формулу имени Олейника». Сразу надо отметить, что он нигде не предоставляет ее источник. Он пишет что де в интернете ее не найти, и вот он ее Показывает (аллилуйя), а где ее взял, он не говорит. Более того, в комментариях его прямо спрашивали — «прошу Вас сообщить в какой из указанных Вами работ в списке литературы указана искомая формула» — в ответ же он лишь намутил воду, объясняя, что де эта формула проще, чем метод Монте-Карло. Отсюда вывод, что эта формула его личный креатив. Ну что ж, давайте взглянем на «Формулу»:
Структура ее понятна: плотность потока частиц nr умножается на их энергию Er (получаем плотность потока энергии — интенсивность излучения), умножается на коэффициент ослабления этой радиации после прохождения через корпус корабля e(...), далее на коэффициент ловли всего этого космонавтом 0.2 и на коэфициент вредности протонов по сравнению с гамма-излучением wr (т.н. коэффициент качества излучения). Получаем дозу в единицу времени (мощность дозы).
Вот что Олейник пишет о коэффициенте 0.2: «Множитель 0,2 перед знаком суммирования имеет размерность м2/кг и представляет собой обратное значение средней эффективной толщины биологической защиты человека. Грубо, данный множитель равен площади поверхности биологического объекта, деленная на шестую часть массы» и «множитель 6 - степени свободы протонов в РПЗ - движение вверх, вниз, влево, вперед, назад и вращение вокруг осей».
Неверно. Это полная чушь. Бездарь Олейник не понимает, что такое плотность потока частиц и на что ее надо умножать.
По Олейнику 0.2 = пл.тела·6/масса. Понятно, что для вычисления дозы радиации надо посчитать сколько всего радиации поймал человек и поделить это на его массу, как верно пишет сам Олейник: «Поглощенная доза (D) - основная дозиметрическая величина. Она равна отношению средней энергии dE, переданной ионизирующим излучением веществу в элементарном объеме, к массе dm вещества в этом объеме: D = dE/dm». Итого, мы получаем, что чтобы получить количество частиц, пойманных космонавтом, плотность потока Олейник умножает на площадь тела и на 6, или, если масса космонавта 75 кг (Олейник не указал используемые им параметры, но масса Армстронга или Олдрина была 75 кг), то это будет 0.2*75 = 15.
Определение плотности потока частиц можно найти в любом учебнике касающемся ионизирующих излучений, я процитирую определение из НРБ-99/2009: «Плотность потока частиц n - отношение dN/(da·dt), где dN - количество частиц, падающих на сферу с площадью поперечного сечения da за интервал времени dt». Итого никакие степени свободы здесь не нужны: в самой величине плотности потока уже учтены все степени свободы — это суммарное количество частиц попадающих в сферу с какой бы то ни было стороны, и, чтобы получить количество частиц, попадающих в сферу, в соответствии с определением надо умножить плотность потока на площадь поперечного сечения этой сферы. Т.е. никакая площадь тела здесь тоже ни при чем. Эти 15 у Олейника физически означают площадь сечения сферы, которая ловит учитываемую радиацию. Посчитаем размер этой сферы при площади поперечного сечения 15 м2. Радиус сферы будет равен (15/pi)1/2 = 2.2 м. Сфера диаметром более четырех метров?! А не многовато ли, космонавт ведь намного меньше?
Посчитаем по-человечески. Космонавты там сидели, рост сидящего человека около 140 см. Это максимальный разумный диаметр сферы, в которую их можно вписать. Так какой тогда получается коэффициент вместо 0.2?
0.72*pi делить на массу 75 = 0.02 ! В десять раз меньше, чем у Олейника!
Итого имеем, что здесь из-за своего полного непонимания, что он считает, Олейник накручивает лишний порядок.
Идем далее. Чтобы получить те значения, как у Олейника, мне пришлось брать коэффициент качества излучения для протонов wr равным десяти. Снова неверно! Олейник действительно приводит такой коэффициент качества в своей таблице со ссылкой на источники, но это коэффициент качества для низкоэнергетических протонов, как у Олейника и указано — для протонов энергиями 5...10 МэВ. Однако коэффициент качества для протонов с ростом их энергий сильно уменьшается. Например, в присутствующей в списке литературы у Олейника книге Относительная биологическая эффективность излучений на стр. 130-134 приведены значения относительной биологической эффективности высокоэнергетического протонного излучения. И она там около единицы:
Вот незадача-то — помещая в свой «список литературы» источник, где относительная биологическая эффективность (ОБЭ) протонов тех энергий, которые считает Олейник, указывается равной единице, а то и менее, сам же Олейник считает за десять. Странно, да?
На сегодняшний день единый коэффициент качества для протонов принят равным двум. Читаем Рекомендации Международной комиссии по радиационной защите от 2007 года (стр 293-294):
(B 117) В последние годы протонное излучение привлекает больше внимания из-за повышенного интереса к оценке доз у экипажей воздушных судов и астронавтов на космических кораблях. В этих случаях, внешнее протонное облучение происходит за счет солнечного и космического излучения. В первичных полях излучения сильно преобладают протоны высоких энергий, а протоны с энергиями около нескольких МэВ имеют малую значимость, даже учитывая повышенную биологическую эффективность при низких энергиях излучения. Пробег низкоэнергетических протонов в ткани мал (пробег протонов в ткани составляет: для энергии 4 МэВ – 0,25 мм; для энергии 10 МэВ – 1,2 мм), и они по большей части поглощаются в коже.
(B 118) Вследствие вышеизложенного было сочтено достаточно точным для обеспечения радиационной защиты принять единое значение wR для протонов любых энергий. При этом уместно положиться на данные для высокоэнергетических протонов как наиболее представительных для полей космического излучения.
(B 119) Существует всего несколько исследований на животных, где имеется информация об ОБЭ высокоэнергетических протонов. В большинстве этих исследований значения измеренной ОБЭ лежат между 1 и 2. Учитывая плотность ионизации в ткани, протоны высоких энергий могут рассматриваться как излучение с низкой ЛПЭ (при среднем значении ЛПЭ намного меньше, чем 10 кэВ/мкм), и, применив функцию Q(L) из Публикации 60 (ICRP, 1991b), средний коэффициент качества для протонов энергией 100 МэВ, полностью остановленных в ткани, будет меньше, чем 1,2 согласно расчетам (ICRP,2003c). При крайне высоких энергиях протонов около 1 ГэВ становится более важной генерация вторичных заряженных частиц в ядерных реакциях, так что средний коэффициент качества возрастает приблизительно до 1,8.
(B 120) Учитывая все аспекты и имеющиеся данные, взвешивающий коэффициент протонов, установленный в новых Рекомендациях, равен 2 (Таблица B.4).
Притом что это единое значение принято просто для упрощения расчетов для гражданских целей, реально же оно зависит от энергии частицы. А на энергиях, на которых у Олейника происходит наибольший вклад радиации (50-500 МэВ) биологическая эффективность протонов находится в минимуме. Вот оценки биологической эффективности протонного излучения на основе современных данных:
Исходя из этого, чтобы оценить дозу в данных расчетах коэффициент качества стоит брать максимум полтора. А чтобы получить результаты Олейника, надо использовать 10! Вот так он накручивает еще один лишний порядок.
Вместе все это приводит к тому, что баклан Олейник сходу промахивается на два порядка. И это только в одном месте.
Итого, если учесть слова Олейника же что «если на траектории Земля-Луна полёт по легенде НАСА проходил выше геомагнитной широты 30 градусов, тогда, согласно универсальному высотному ходу интенсивности потоков протонов, дозы радиации можно уменьшить на порядок», то при пролете через внутренний пояс мы имеем вовсе не 5 жутких Зивертов, а около... 0.8 бэр. Это если все остальное у Олейника принять на веру. А с остальным там дела так же плохи, можно сказать живого места нет.
Вот сравнение доз радиации при пролете через протонный пояс предоставленных Олейником и пересчитанных мною по его «данным» и «формуле». Как видно, у меня воспроизвелись его цифры, что значит что я верно понял как он их получил:
code text
- МэВ Олейник Я
- 1000 0,00 0.02
- 500 0,19 0.18
- 200 0,60 0.61
- 170 2,23 2.42 (здесь почему-то немного не сошлось)
- 105 2,00 1.62 (здесь почему-то немного не сошлось)
- 50 0,27 0.25
- 30 0,00 0.01
- 20 0,00 0.00
Теперь рассмотрим эту самую «формулу имени Олейника». Сразу надо отметить, что он нигде не предоставляет ее источник. Он пишет что де в интернете ее не найти, и вот он ее Показывает (аллилуйя), а где ее взял, он не говорит. Более того, в комментариях его прямо спрашивали — «прошу Вас сообщить в какой из указанных Вами работ в списке литературы указана искомая формула» — в ответ же он лишь намутил воду, объясняя, что де эта формула проще, чем метод Монте-Карло. Отсюда вывод, что эта формула его личный креатив. Ну что ж, давайте взглянем на «Формулу»:
Н = 0,2·wr·nr·Er·e(...)
Структура ее понятна: плотность потока частиц nr умножается на их энергию Er (получаем плотность потока энергии — интенсивность излучения), умножается на коэффициент ослабления этой радиации после прохождения через корпус корабля e(...), далее на коэффициент ловли всего этого космонавтом 0.2 и на коэфициент вредности протонов по сравнению с гамма-излучением wr (т.н. коэффициент качества излучения). Получаем дозу в единицу времени (мощность дозы).
Вот что Олейник пишет о коэффициенте 0.2: «Множитель 0,2 перед знаком суммирования имеет размерность м2/кг и представляет собой обратное значение средней эффективной толщины биологической защиты человека. Грубо, данный множитель равен площади поверхности биологического объекта, деленная на шестую часть массы» и «множитель 6 - степени свободы протонов в РПЗ - движение вверх, вниз, влево, вперед, назад и вращение вокруг осей».
Неверно. Это полная чушь. Бездарь Олейник не понимает, что такое плотность потока частиц и на что ее надо умножать.
По Олейнику 0.2 = пл.тела·6/масса. Понятно, что для вычисления дозы радиации надо посчитать сколько всего радиации поймал человек и поделить это на его массу, как верно пишет сам Олейник: «Поглощенная доза (D) - основная дозиметрическая величина. Она равна отношению средней энергии dE, переданной ионизирующим излучением веществу в элементарном объеме, к массе dm вещества в этом объеме: D = dE/dm». Итого, мы получаем, что чтобы получить количество частиц, пойманных космонавтом, плотность потока Олейник умножает на площадь тела и на 6, или, если масса космонавта 75 кг (Олейник не указал используемые им параметры, но масса Армстронга или Олдрина была 75 кг), то это будет 0.2*75 = 15.
Определение плотности потока частиц можно найти в любом учебнике касающемся ионизирующих излучений, я процитирую определение из НРБ-99/2009: «Плотность потока частиц n - отношение dN/(da·dt), где dN - количество частиц, падающих на сферу с площадью поперечного сечения da за интервал времени dt». Итого никакие степени свободы здесь не нужны: в самой величине плотности потока уже учтены все степени свободы — это суммарное количество частиц попадающих в сферу с какой бы то ни было стороны, и, чтобы получить количество частиц, попадающих в сферу, в соответствии с определением надо умножить плотность потока на площадь поперечного сечения этой сферы. Т.е. никакая площадь тела здесь тоже ни при чем. Эти 15 у Олейника физически означают площадь сечения сферы, которая ловит учитываемую радиацию. Посчитаем размер этой сферы при площади поперечного сечения 15 м2. Радиус сферы будет равен (15/pi)1/2 = 2.2 м. Сфера диаметром более четырех метров?! А не многовато ли, космонавт ведь намного меньше?
Посчитаем по-человечески. Космонавты там сидели, рост сидящего человека около 140 см. Это максимальный разумный диаметр сферы, в которую их можно вписать. Так какой тогда получается коэффициент вместо 0.2?
0.72*pi делить на массу 75 = 0.02 ! В десять раз меньше, чем у Олейника!
И, разумеется, космонавты будут хватать в разы меньшее количество радиации, чем попадает в эту сферу, поскольку сами меньше. 0.02 это сильно завышенная оценка. На самом деле можно использовать не сечение сферы, а максимальную площадь сечения космонавта, и т.о. взять максимальную площадь силуэта сидящего космонавта (т.е. в анфас) и получить коэффициент (все еще завышенный!) менее чем 0.01. Но не будем утомлять этими уточнениями поциентов.
Итого имеем, что здесь из-за своего полного непонимания, что он считает, Олейник накручивает лишний порядок.
Идем далее. Чтобы получить те значения, как у Олейника, мне пришлось брать коэффициент качества излучения для протонов wr равным десяти. Снова неверно! Олейник действительно приводит такой коэффициент качества в своей таблице со ссылкой на источники, но это коэффициент качества для низкоэнергетических протонов, как у Олейника и указано — для протонов энергиями 5...10 МэВ. Однако коэффициент качества для протонов с ростом их энергий сильно уменьшается. Например, в присутствующей в списке литературы у Олейника книге Относительная биологическая эффективность излучений на стр. 130-134 приведены значения относительной биологической эффективности высокоэнергетического протонного излучения. И она там около единицы:
Вот незадача-то — помещая в свой «список литературы» источник, где относительная биологическая эффективность (ОБЭ) протонов тех энергий, которые считает Олейник, указывается равной единице, а то и менее, сам же Олейник считает за десять. Странно, да?
На сегодняшний день единый коэффициент качества для протонов принят равным двум. Читаем Рекомендации Международной комиссии по радиационной защите от 2007 года (стр 293-294):
(B 117) В последние годы протонное излучение привлекает больше внимания из-за повышенного интереса к оценке доз у экипажей воздушных судов и астронавтов на космических кораблях. В этих случаях, внешнее протонное облучение происходит за счет солнечного и космического излучения. В первичных полях излучения сильно преобладают протоны высоких энергий, а протоны с энергиями около нескольких МэВ имеют малую значимость, даже учитывая повышенную биологическую эффективность при низких энергиях излучения. Пробег низкоэнергетических протонов в ткани мал (пробег протонов в ткани составляет: для энергии 4 МэВ – 0,25 мм; для энергии 10 МэВ – 1,2 мм), и они по большей части поглощаются в коже.
(B 118) Вследствие вышеизложенного было сочтено достаточно точным для обеспечения радиационной защиты принять единое значение wR для протонов любых энергий. При этом уместно положиться на данные для высокоэнергетических протонов как наиболее представительных для полей космического излучения.
(B 119) Существует всего несколько исследований на животных, где имеется информация об ОБЭ высокоэнергетических протонов. В большинстве этих исследований значения измеренной ОБЭ лежат между 1 и 2. Учитывая плотность ионизации в ткани, протоны высоких энергий могут рассматриваться как излучение с низкой ЛПЭ (при среднем значении ЛПЭ намного меньше, чем 10 кэВ/мкм), и, применив функцию Q(L) из Публикации 60 (ICRP, 1991b), средний коэффициент качества для протонов энергией 100 МэВ, полностью остановленных в ткани, будет меньше, чем 1,2 согласно расчетам (ICRP,2003c). При крайне высоких энергиях протонов около 1 ГэВ становится более важной генерация вторичных заряженных частиц в ядерных реакциях, так что средний коэффициент качества возрастает приблизительно до 1,8.
(B 120) Учитывая все аспекты и имеющиеся данные, взвешивающий коэффициент протонов, установленный в новых Рекомендациях, равен 2 (Таблица B.4).
Притом что это единое значение принято просто для упрощения расчетов для гражданских целей, реально же оно зависит от энергии частицы. А на энергиях, на которых у Олейника происходит наибольший вклад радиации (50-500 МэВ) биологическая эффективность протонов находится в минимуме. Вот оценки биологической эффективности протонного излучения на основе современных данных:
Исходя из этого, чтобы оценить дозу в данных расчетах коэффициент качества стоит брать максимум полтора. А чтобы получить результаты Олейника, надо использовать 10! Вот так он накручивает еще один лишний порядок.
Вместе все это приводит к тому, что баклан Олейник сходу промахивается на два порядка. И это только в одном месте.
Итого, если учесть слова Олейника же что «если на траектории Земля-Луна полёт по легенде НАСА проходил выше геомагнитной широты 30 градусов, тогда, согласно универсальному высотному ходу интенсивности потоков протонов, дозы радиации можно уменьшить на порядок», то при пролете через внутренний пояс мы имеем вовсе не 5 жутких Зивертов, а около... 0.8 бэр. Это если все остальное у Олейника принять на веру. А с остальным там дела так же плохи, можно сказать живого места нет.
Иногда Сатурн-5 это просто Сатурн-5




Это сообщение редактировалось 06.08.2015 в 09:17
dr.Mengele> Определение плотности потока частиц можно найти в любом учебнике касающемся ионизирующих излучений, я процитирую определение из НРБ-99/2009: «Плотность потока частиц n - отношение dN/(da·dt), где dN - количество частиц, падающих на сферу с площадью поперечного сечения da за интервал времени dt». Итого никакие степени свободы здесь не нужны: в самой величине плотности потока уже учтены все степени свободы — это суммарное количество частиц попадающих в сферу с какой бы то ни было стороны, и, чтобы получить количество частиц, попадающих в сферу, в соответствии с определением надо умножить плотность потока на площадь поперечного сечения этой сферы. Т.е. никакая площадь тела здесь тоже ни при чем. Эти 15 у Олейника физически означают площадь сечения сферы, которая ловит учитываемую радиацию. Посчитаем размер этой сферы при площади поперечного сечения 15 м2. Радиус сферы будет равен (15/pi)1/2 = 2.2 м. Сфера диаметром более четырех метров?! А не многовато ли, космонавт ведь намного меньше?
dr.Mengele> чтобы получить количество частиц, попадающих в сферу, в соответствии с определением надо умножить плотность потока на площадь поперечного сечения этой сферы.
Очевидно, что это относится к направленному излучению.
Радиация в космосе складывается из двух источников: солнечное излучение и галактическое излучение.
Радиацию от солнечного излучения можно считать, как плотность потока, умноженную на площадь поперечного (а, может, продольного?) сечения сферы.
Радиация от галактического излучения считается, как плотность потока, умноженная на площадь поверхности сферы, т.е, в 4 раза больше.
Так что, пересчитывайте все заново, отдельно - по солнечному излучению и отдельно - по галактическому.
dr.Mengele> чтобы получить количество частиц, попадающих в сферу, в соответствии с определением надо умножить плотность потока на площадь поперечного сечения этой сферы.
Очевидно, что это относится к направленному излучению.
Радиация в космосе складывается из двух источников: солнечное излучение и галактическое излучение.
Радиацию от солнечного излучения можно считать, как плотность потока, умноженную на площадь поперечного (а, может, продольного?) сечения сферы.
Радиация от галактического излучения считается, как плотность потока, умноженная на площадь поверхности сферы, т.е, в 4 раза больше.
Так что, пересчитывайте все заново, отдельно - по солнечному излучению и отдельно - по галактическому.


dr.Mengele>> чтобы получить количество частиц, попадающих в сферу, в соответствии с определением надо умножить плотность потока на площадь поперечного сечения этой сферы.
E.V.> Очевидно, что это относится к направленному излучению.
Очевидно что вы, как и Олейник, не понимаете, что такое плотность потока частиц. Количество частиц, прошедших через сферу, при данной плотности потока будет считаться независимо от того, имеет ли этот поток направление или же он изотропен, и считается умножением плотности потока на площадь ее поперечного сечения. А вот количество частиц, пересекших некий конкретным образом расположенный в пространстве круг — будет зависеть от направленности потока и просто по одной скалярной величине плотности потока посчитано быть не может.
E.V.> Радиация в космосе складывается из двух источников: солнечное излучение и галактическое излучение.
Вы даже не поняли, о чем речь — считается радиация при пересечении внутреннего пояса Ван Аллена (на основе посчитанных Олейником же исходных данных), а не от солнечных и не от галактических лучей.
E.V.> Радиацию от солнечного излучения можно считать, как плотность потока, умноженную на площадь поперечного (а, может, продольного?) сечения сферы.
E.V.> Радиация от галактического излучения считается, как плотность потока, умноженная на площадь поверхности сферы, т.е, в 4 раза больше.
Послушайте, а когда вы считаете объем цилиндра скажем, вы тоже в одном случае высоту умножаете на площадь основания, а в другом — на длину периметра?
E.V.> Радиация от галактического излучения считается, как плотность потока, умноженная на площадь поверхности сферы, т.е, в 4 раза больше.
Сами придумали? Хоть один вменяемый источник сможете найти? Вы понимаете что то, что надо умножать на площадь сферы это уже будет не плотность потока, а что-то другое, просто по определению плотности потока?
E.V.> Так что, пересчитывайте все заново
Смеетесь? Разберитесь сначала, о чем здесь вообще речь, ознакомьтесь с определениями используемых понятий.
E.V.> отдельно - по солнечному излучению и отдельно - по галактическому.
Здесь не считается ни то, ни другое.
E.V.> Очевидно, что это относится к направленному излучению.
Очевидно что вы, как и Олейник, не понимаете, что такое плотность потока частиц. Количество частиц, прошедших через сферу, при данной плотности потока будет считаться независимо от того, имеет ли этот поток направление или же он изотропен, и считается умножением плотности потока на площадь ее поперечного сечения. А вот количество частиц, пересекших некий конкретным образом расположенный в пространстве круг — будет зависеть от направленности потока и просто по одной скалярной величине плотности потока посчитано быть не может.
E.V.> Радиация в космосе складывается из двух источников: солнечное излучение и галактическое излучение.
Вы даже не поняли, о чем речь — считается радиация при пересечении внутреннего пояса Ван Аллена (на основе посчитанных Олейником же исходных данных), а не от солнечных и не от галактических лучей.
E.V.> Радиацию от солнечного излучения можно считать, как плотность потока, умноженную на площадь поперечного (а, может, продольного?) сечения сферы.
E.V.> Радиация от галактического излучения считается, как плотность потока, умноженная на площадь поверхности сферы, т.е, в 4 раза больше.
Послушайте, а когда вы считаете объем цилиндра скажем, вы тоже в одном случае высоту умножаете на площадь основания, а в другом — на длину периметра?
E.V.> Радиация от галактического излучения считается, как плотность потока, умноженная на площадь поверхности сферы, т.е, в 4 раза больше.
Сами придумали? Хоть один вменяемый источник сможете найти? Вы понимаете что то, что надо умножать на площадь сферы это уже будет не плотность потока, а что-то другое, просто по определению плотности потока?
E.V.> Так что, пересчитывайте все заново
Смеетесь? Разберитесь сначала, о чем здесь вообще речь, ознакомьтесь с определениями используемых понятий.
E.V.> отдельно - по солнечному излучению и отдельно - по галактическому.
Здесь не считается ни то, ни другое.
Иногда Сатурн-5 это просто Сатурн-5




Это сообщение редактировалось 08.08.2015 в 17:25
dr.Mengele> Очевидно что вы, как и Олейник, не понимаете, что такое плотность потока частиц. Количество частиц, прошедших через сферу, при данной плотности потока будет считаться независимо от того, имеет ли этот поток направление или же он изотропен, и считается умножением плотности потока на площадь ее поперечного сечения. А вот количество частиц, пересекших некий конкретным образом расположенный в пространстве круг — будет зависеть от направленности потока и просто по одной скалярной величине плотности потока посчитано быть не может.
Я думал: это серьезный специалист нарисовался. А это какой-то даже не ботаник, а недоботаник.
Набирайте в поисковике браузера "плотность потока" и вдумчиво читайте все статьи подряд.
И, вообще, лучше бы вы напрямую с лига-спейсом разбирались. Один другого стоит.
Я думал: это серьезный специалист нарисовался. А это какой-то даже не ботаник, а недоботаник.
Набирайте в поисковике браузера "плотность потока" и вдумчиво читайте все статьи подряд.
И, вообще, лучше бы вы напрямую с лига-спейсом разбирались. Один другого стоит.


E.V.> Набирайте в поисковике браузера "плотность потока" и вдумчиво читайте все статьи подряд.
Я-то как бе уже и давно, и не столько статьи, сколько книги и учебники. И все у меня правильно. А вам могу еще раз повторить определение плотности потока частиц из НРБ-99/2009: «Плотность потока частиц n - отношение dN/(da·dt), где dN - количество частиц, падающих на сферу с площадью поперечного сечения da за интервал времени dt».
Отсего на что надо умножить n чтобы получить dN в единицу времени? На площадь сферы? Нет, на площадь ее поперечного сечения da.
А вот вам как раз стоит набрать в поисковике «плотность потока частиц» и попробовать найти какое-то свое, «правильное» определение. Если получится.
Я-то как бе уже и давно, и не столько статьи, сколько книги и учебники. И все у меня правильно. А вам могу еще раз повторить определение плотности потока частиц из НРБ-99/2009: «Плотность потока частиц n - отношение dN/(da·dt), где dN - количество частиц, падающих на сферу с площадью поперечного сечения da за интервал времени dt».
Отсего на что надо умножить n чтобы получить dN в единицу времени? На площадь сферы? Нет, на площадь ее поперечного сечения da.
А вот вам как раз стоит набрать в поисковике «плотность потока частиц» и попробовать найти какое-то свое, «правильное» определение. Если получится.
Иногда Сатурн-5 это просто Сатурн-5




dr.Mengele> Я-то как бе уже и давно, и не столько статьи, сколько книги и учебники. И все у меня правильно.
Смотрите в книгу, а видите фигу.
dr.Mengele> А вам могу еще раз повторить определение плотности потока частиц из НРБ-99/2009: «Плотность потока частиц n - отношение dN/(da·dt), где dN - количество частиц, падающих на сферу с площадью поперечного сечения da за интервал времени dt».
dr.Mengele> Отсего на что надо умножить n чтобы получить dN в единицу времени? На площадь сферы? Нет, на площадь ее поперечного сечения da.
Да не умножить, а разделить!
С детства ненавижу формулы типа "х=dy" (так же, как и килограмм-силы). Вот и вы вляпались.
Давайте посмотрим определение не из НРБ а из вики
Ключевое слово здесь - элементарная сфера.
Речь идет об элементарной точке поверхности. Т.е, для элементарной точки поверхности радиусом, например, 1 мм считается количество частиц, упавших на сферу радиусом 1 мм (но величины выражены в метрах).
Вы считаете количество облучения, полученное каким-то телом, что будет равно плотности потока, умноженной на площадь поверхности тела (уже не элементарной, а реальной геометрической). Если тело - сфера, то количество облучения - плотность потока, умноженная на площадь поверхности сферы.
Немножко понятно?
P.S.
Сам я считаю, что составители НРБ, увлекшись своими dx и dy, реальную геометрическую картину получения телом радиации исказили.
Смотрите в книгу, а видите фигу.
dr.Mengele> А вам могу еще раз повторить определение плотности потока частиц из НРБ-99/2009: «Плотность потока частиц n - отношение dN/(da·dt), где dN - количество частиц, падающих на сферу с площадью поперечного сечения da за интервал времени dt».
dr.Mengele> Отсего на что надо умножить n чтобы получить dN в единицу времени? На площадь сферы? Нет, на площадь ее поперечного сечения da.
Да не умножить, а разделить!
С детства ненавижу формулы типа "х=dy" (так же, как и килограмм-силы). Вот и вы вляпались.
Давайте посмотрим определение не из НРБ а из вики
флюенсФлюенсом частиц в случае пучка частиц называют отношение числа частиц dN, пересёкших перпендикулярную пучку элементарную площадку dS за данный промежуток времени, к площади этой площадки. В случае диффузного поля частиц, флюенс в точке определяется как отношение числа частиц, проникших в элементарную сферу с центром в этой точке, к площади поперечного сечения этой сферы.
Единицы измерения — м−2 (СИ), см−2 (СГС). 1 м−2 — такой флюенс, при котором в объём сферы с площадью поперечного сечения 1 м² попадает одна частица.
Мощность флюенса частиц (плотность потока частиц) определяется как производная по времени от флюенса, накопленного за время t:
Ключевое слово здесь - элементарная сфера.
Речь идет об элементарной точке поверхности. Т.е, для элементарной точки поверхности радиусом, например, 1 мм считается количество частиц, упавших на сферу радиусом 1 мм (но величины выражены в метрах).
Вы считаете количество облучения, полученное каким-то телом, что будет равно плотности потока, умноженной на площадь поверхности тела (уже не элементарной, а реальной геометрической). Если тело - сфера, то количество облучения - плотность потока, умноженная на площадь поверхности сферы.
Немножко понятно?
P.S.
Сам я считаю, что составители НРБ, увлекшись своими dx и dy, реальную геометрическую картину получения телом радиации исказили.


Это сообщение редактировалось 09.08.2015 в 11:02
E.V.> Да не умножить, а разделить!
В арифметике даже путаетесь! У вас же тогда получится, что чем больше сфера, тем меньше через нее проходит частиц при данном потоке. Абсурд.
E.V.> С детства ненавижу формулы типа "х=dy" (так же, как и килограмм-силы). Вот и вы вляпались.
Чушь не несите. Вы местное тролололо что ли?
E.V.> Ключевое слово здесь - элементарная сфера.
И что же такое здесь «элементарная сфера»? Нашли определение, или опять из головы вытаскиваете ерунду?
E.V.> Т.е, для элементарной точки поверхности радиусом, например, 1 мм считается количество частиц, упавших на сферу радиусом 1 мм (но величины выражены в метрах).
И для сферы радиусом 1 мм, разумеется, тоже будет работать определение, да.
E.V.> Вы считаете количество облучения, полученное каким-то телом, что будет равно плотности потока, умноженной на площадь поверхности тела
Я вам повторяю, сослаться на что-либо можете кроме собственных бредней? Читайте определение. Никакая площадь поверхности тела там не фигурирует вообще. Если слово «элементарная» будит ваше шальное воображение, то поищите определение, что такое элементарная сфера, а не порите чушь.
E.V.> Если тело - сфера, то количество облучения - плотность потока, умноженная на площадь поверхности сферы.
А почему не на объем тогда? Или не на удвоенную площадь поверхности? Откуда вы взяли свою бредятинку?
Читайте определение. Четко сказано, что плотность потока это отношение числа частиц, попавших в сферу, к площади ее поперечного сечения (в единицу времени). Никакая площадь поверхности здесь не фигурирует.
E.V.> Немножко понятно?
Понятно что вы не понимаете, о чем речь, и склонны к фантазиям и пустословию.
E.V.> P.S.
E.V.> Сам я считаю, что составители НРБ, увлекшись своими dx и dy, реальную геометрическую картину получения телом радиации исказили.
Там все правильно.
В арифметике даже путаетесь! У вас же тогда получится, что чем больше сфера, тем меньше через нее проходит частиц при данном потоке. Абсурд.
E.V.> С детства ненавижу формулы типа "х=dy" (так же, как и килограмм-силы). Вот и вы вляпались.
Чушь не несите. Вы местное тролололо что ли?
E.V.> Ключевое слово здесь - элементарная сфера.
И что же такое здесь «элементарная сфера»? Нашли определение, или опять из головы вытаскиваете ерунду?
E.V.> Т.е, для элементарной точки поверхности радиусом, например, 1 мм считается количество частиц, упавших на сферу радиусом 1 мм (но величины выражены в метрах).
И для сферы радиусом 1 мм, разумеется, тоже будет работать определение, да.
E.V.> Вы считаете количество облучения, полученное каким-то телом, что будет равно плотности потока, умноженной на площадь поверхности тела
Я вам повторяю, сослаться на что-либо можете кроме собственных бредней? Читайте определение. Никакая площадь поверхности тела там не фигурирует вообще. Если слово «элементарная» будит ваше шальное воображение, то поищите определение, что такое элементарная сфера, а не порите чушь.
E.V.> Если тело - сфера, то количество облучения - плотность потока, умноженная на площадь поверхности сферы.
А почему не на объем тогда? Или не на удвоенную площадь поверхности? Откуда вы взяли свою бредятинку?
Читайте определение. Четко сказано, что плотность потока это отношение числа частиц, попавших в сферу, к площади ее поперечного сечения (в единицу времени). Никакая площадь поверхности здесь не фигурирует.
E.V.> Немножко понятно?
Понятно что вы не понимаете, о чем речь, и склонны к фантазиям и пустословию.
E.V.> P.S.
E.V.> Сам я считаю, что составители НРБ, увлекшись своими dx и dy, реальную геометрическую картину получения телом радиации исказили.
Там все правильно.
Иногда Сатурн-5 это просто Сатурн-5




E.V.> Живи, как знаешь
Все же советую ознакомиться с тем, что называется здесь «элементарной сферой». Или спросить меня, если сам не можешь разобраться. Википедия... Книжку открой.
Все же советую ознакомиться с тем, что называется здесь «элементарной сферой». Или спросить меня, если сам не можешь разобраться. Википедия... Книжку открой.
Иногда Сатурн-5 это просто Сатурн-5




E.V.> Поздравляю защитников-НАСАрогов с ценным пополнением!
Так что же называется здесь элементарной сферой-то, а? Разобрался, горе-умник?
Так что же называется здесь элементарной сферой-то, а? Разобрался, горе-умник?
Иногда Сатурн-5 это просто Сатурн-5




Little_boo
новичок
E.V.>> Поздравляю защитников-НАСАрогов с ценным пополнением!
dr.Mengele> Так что же называется здесь элементарной сферой-то, а? Разобрался, горе-умник?
Я вот такое определение нашел:
ИНТЕНСИВНОСТЬ ИЗЛУЧЕНИЯ (интенсивность лучистого потока), полный поток энергии излучения, проходящий за ед. времени через единичную площадку в направлении нормали к ней и рассчитанный на ед. телесного угла.
Мне кажется, или вы об одном и том же спорите. Всё что вошло через поверхность, пройдет и через её сечение. Это если про сферу в вакууме, а для человека, действительно логичнее говорить о площади. Ведь частицы поглощаются тканями.
В любом случае как не считай зачем на 6 умножать?
dr.Mengele> Так что же называется здесь элементарной сферой-то, а? Разобрался, горе-умник?
Я вот такое определение нашел:
ИНТЕНСИВНОСТЬ ИЗЛУЧЕНИЯ (интенсивность лучистого потока), полный поток энергии излучения, проходящий за ед. времени через единичную площадку в направлении нормали к ней и рассчитанный на ед. телесного угла.
Мне кажется, или вы об одном и том же спорите. Всё что вошло через поверхность, пройдет и через её сечение. Это если про сферу в вакууме, а для человека, действительно логичнее говорить о площади. Ведь частицы поглощаются тканями.
В любом случае как не считай зачем на 6 умножать?


Как то вы вдруг, негаданно-нежданно...
L.b.> Я вот такое определение нашел:
L.b.> ИНТЕНСИВНОСТЬ ИЗЛУЧЕНИЯ (интенсивность лучистого потока), полный поток энергии излучения, проходящий за ед. времени через единичную площадку в направлении нормали к ней и рассчитанный на ед. телесного угла.
L.b.> Мне кажется, или вы об одном и том же спорите. Всё что вошло через поверхность, пройдет и через её сечение. Это если про сферу в вакууме, а для человека, действительно логичнее говорить о площади. Ведь частицы поглощаются тканями.
L.b.> В любом случае как не считай зачем на 6 умножать?
Зачем на 6 умножать, я не знаю. В остальном давайте попробуем разобраться.
Вот, что я цитировал:
Обратите внимание: в обоих случаях имеется ввиду количество частиц падающих на элементарную площадку по нормали.
Теперь дальше - то, на что вы не обратили внимания:
Если, в вашем случае на элементарную площадку радиусом 1 мм за 1 с попадет 3 частицы, то плотность потока будет 3/3=1 частица*с/мм.кв. Если в случае диффузного поля на элементарную сферу радиусом 1 мм попадет 3 частицы, то плотность потока тоже будет 3/3=1 частица*с/мм.кв.
Если захотим узнать какое облучение получит в диффузном поле какой-нибудь космический колобок, нужно плотность потока умножить на время экспозиции и на площадь поверхности колобка. А площадь поверхности колобка и будет 4*Пи*R2
Как то так.
L.b.> Я вот такое определение нашел:
L.b.> ИНТЕНСИВНОСТЬ ИЗЛУЧЕНИЯ (интенсивность лучистого потока), полный поток энергии излучения, проходящий за ед. времени через единичную площадку в направлении нормали к ней и рассчитанный на ед. телесного угла.
L.b.> Мне кажется, или вы об одном и том же спорите. Всё что вошло через поверхность, пройдет и через её сечение. Это если про сферу в вакууме, а для человека, действительно логичнее говорить о площади. Ведь частицы поглощаются тканями.
L.b.> В любом случае как не считай зачем на 6 умножать?
Зачем на 6 умножать, я не знаю. В остальном давайте попробуем разобраться.
Вот, что я цитировал:
Ничего не напоминает? Например, ваше определение?Флюенсом частиц в случае пучка частиц называют отношение числа частиц dN, пересёкших перпендикулярную пучку элементарную площадку dS за данный промежуток времени, к площади этой площадки.
Обратите внимание: в обоих случаях имеется ввиду количество частиц падающих на элементарную площадку по нормали.
Теперь дальше - то, на что вы не обратили внимания:
т.е, учитываются частицы с любого направления.В случае диффузного поля частиц, флюенс в точке определяется как отношение числа частиц, проникших в элементарную сферу с центром в этой точке, к площади поперечного сечения этой сферы.
Если, в вашем случае на элементарную площадку радиусом 1 мм за 1 с попадет 3 частицы, то плотность потока будет 3/3=1 частица*с/мм.кв. Если в случае диффузного поля на элементарную сферу радиусом 1 мм попадет 3 частицы, то плотность потока тоже будет 3/3=1 частица*с/мм.кв.
Если захотим узнать какое облучение получит в диффузном поле какой-нибудь космический колобок, нужно плотность потока умножить на время экспозиции и на площадь поверхности колобка. А площадь поверхности колобка и будет 4*Пи*R2
Как то так.


E.V.> Если захотим узнать какое облучение получит в диффузном поле какой-нибудь космический колобок, нужно плотность потока умножить на время экспозиции и на площадь поверхности колобка. А площадь поверхности колобка и будет 4*Пи*R2
E.V.> Как то так.
Нет, нам нужно умножить на разницу размеров единичного колобка (относительно которого поток меряли) и нашего.
Т.е просто на R2
E.V.> Как то так.
Нет, нам нужно умножить на разницу размеров единичного колобка (относительно которого поток меряли) и нашего.
Т.е просто на R2

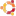
E.V.> Даже без "Пи", хотя бы одного? Странно это как то...
Считается, что к площади поперечного сечения (Пи*R2) но реально - прошедших через поверхность этой сферы (4*Пи*R2)
В случае диффузного поля частиц, флюенс в точке определяется как отношение числа частиц, проникших в элементарную сферу с центром в этой точке, к площади поперечного сечения этой сферы.
Считается, что к площади поперечного сечения (Пи*R2) но реально - прошедших через поверхность этой сферы (4*Пи*R2)

В случае диффузного поля частиц, флюенс в точке определяется как отношение числа частиц, проникших в элементарную сферу с центром в этой точке, к площади поперечного сечения этой сферы.
Дем> Считается, что к площади поперечного сечения (Пи*R2) но реально - прошедших через поверхность этой сферы (4*Пи*R2)
Во-первых, реально - через поверхность полусферы.
элементарная точка находится на какой-то поверхности, поэтому половина "элементарной" сферы будет отрезана этой самой поверхностью.
Во-вторых, реально - через поверхность полусферы любого размера, но направленных к центру полусферы.
В-третьих, цитируемое определение (не знаю, кто сочинял), хоть и звучит очень "Вумно", является совершенно бестолковым. По-моему правильно было бы что-то вроде: "числа частиц, попавших на элементарную точку (или площадку) из телесного угла 2 Пи стерадиан".
В-четвертых, чтобы все это было понятней предлагаю нарисовать элементарную схемку:
в середине листа формата А4 ставим точку (это наша элементарная точка, она же сфера). Из этой точки строим окружность R=1мм (та же точка, но имеющая размеры). Из центральной точки строим окружность R=100 мм. Это - небесная сфера. От этой сферы малюем массу прямых во всех направлениях.
видим, что через нашу "элементарную" сферу проходят только те прямые, которые направлены к центру сферы. Следовательно, имеет значение только телесный угол, а не размер элементарной сферы.
Вроде, дальше разжевывать уже некуда...


Чтобы не потерялось, оставлю здесь пару ссылок.
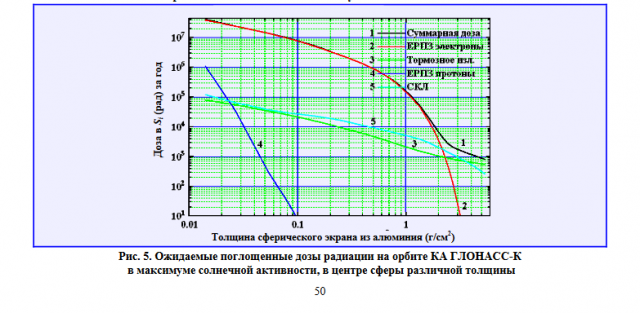
1) В интернете выложена книга: И.В. Гецелев, А.И. Зубарев, О.Л. Пудовкин. Радиационная обстановка на борту космических аппаратов // ЦИПК, 2001.
Рисунок на стр. 83 позволяет грубо оценивать дозы при пролете радиационных поясов:
Очень приблизительно: летели через протонный пояс около 20 мин = 1/72 суток, в пике будет ~200 рад/сутки за защитой 5 г/см2, значит, при пролете в экваториальной плоскости накопится ~3 рад. На самом деле, конечно, меньше. Но и отсюда уже понятно, что Олейник завышает дозы на 3 порядка.
2) Испытуемые утверждают, что в книге не учитывается доза от тормозного излучения электронов при прохождении внешнего пояса. На самом деле, видимо, учитывается (поскольку приведена методика расчета), но явно об этом не сказано. Откроем статью: А.Е. Шилов, С.Н. Волков, И.П. Безродных, В.Т. Семенов. РАДИАЦИОННЫЕ УСЛОВИЯ ДЛЯ ВЫСОКООРБИТАЛЬНЫХ КОСМИЧЕСКИХ АППАРАТОВ В ПЕРИОД МАКСИМУМА СОЛНЕЧНОЙ АКТИВНОСТИ // Труды ВНИИЭМ, 2010.
Выясняется, что поглощенная доза на орбите КА ГЛОНАСС (который 4 раза в сутки проходит внешний пояс на высоте 19 тыс км. в плоскости геомагнитного экватора, составляет ~1000 рад/год (защита 5 г/см2). Т.е. менее 1 рад за половину витка.
Таким образом, если лететь прямо через радиационные пояса при максимуме солнечной активности и с защитой более 5 г/см2 алюминия, вероятно, можно получить дозу в единицы рад, но никак не в тысячи. "Аполлоны" не проходили через максимум интенсивности излучения. Кроме того, во время полета А-14 (и более поздних миссий) солнечная активность была уже на спаде.
1) В интернете выложена книга: И.В. Гецелев, А.И. Зубарев, О.Л. Пудовкин. Радиационная обстановка на борту космических аппаратов // ЦИПК, 2001.
Рисунок на стр. 83 позволяет грубо оценивать дозы при пролете радиационных поясов:
Очень приблизительно: летели через протонный пояс около 20 мин = 1/72 суток, в пике будет ~200 рад/сутки за защитой 5 г/см2, значит, при пролете в экваториальной плоскости накопится ~3 рад. На самом деле, конечно, меньше. Но и отсюда уже понятно, что Олейник завышает дозы на 3 порядка.
2) Испытуемые утверждают, что в книге не учитывается доза от тормозного излучения электронов при прохождении внешнего пояса. На самом деле, видимо, учитывается (поскольку приведена методика расчета), но явно об этом не сказано. Откроем статью: А.Е. Шилов, С.Н. Волков, И.П. Безродных, В.Т. Семенов. РАДИАЦИОННЫЕ УСЛОВИЯ ДЛЯ ВЫСОКООРБИТАЛЬНЫХ КОСМИЧЕСКИХ АППАРАТОВ В ПЕРИОД МАКСИМУМА СОЛНЕЧНОЙ АКТИВНОСТИ // Труды ВНИИЭМ, 2010.
Выясняется, что поглощенная доза на орбите КА ГЛОНАСС (который 4 раза в сутки проходит внешний пояс на высоте 19 тыс км. в плоскости геомагнитного экватора, составляет ~1000 рад/год (защита 5 г/см2). Т.е. менее 1 рад за половину витка.
Таким образом, если лететь прямо через радиационные пояса при максимуме солнечной активности и с защитой более 5 г/см2 алюминия, вероятно, можно получить дозу в единицы рад, но никак не в тысячи. "Аполлоны" не проходили через максимум интенсивности излучения. Кроме того, во время полета А-14 (и более поздних миссий) солнечная активность была уже на спаде.


Это сообщение редактировалось 08.01.2017 в 09:54
Copyright © Balancer 1997..2018
Создано 06.08.2015
Связь с владельцами и администрацией сайта: anonisimov@gmail.com, rwasp1957@yandex.ru и admin@balancer.ru.
Создано 06.08.2015
Связь с владельцами и администрацией сайта: anonisimov@gmail.com, rwasp1957@yandex.ru и admin@balancer.ru.
/7213de79b2c4d639f0cf7961ee32d674.png)
 dr.Mengele
dr.Mengele



 инфо
инфо инструменты
инструменты