 Реклама Google — средство выживания форумов :)
Реклама Google — средство выживания форумов :)
-
![[image]](https://www.balancer.ru/cache/uploads/images/1247/128x128-crop/1247591-0002-001-pervyj-iskusstvennyj-sputnik-zemli.png)
Эксперимент на лоренцево сокращение
Кольцо на орбитеТеги:
Начнем с космического эксперимента, спутник на орбите.
Тут всё понятно из-за линейной скорости V (V=wR) спутник будет испытывать лоренцево сжатие, которое никак не заметят, находящиеся в нем приборы.
Теперь усложним опыт. Пусть спутников много и они занимают всю окружность орбиты, опять ничего не изменилось, каждый спутник испытывает лоренцево сжатие.
Но теперь соединим спутники пружинами или заменим на орбитальное кольцо. Каждый спутник и сама пружина испытывает сокращение, но при этом их тянет пружина, поэтому возникнет сила, действующая на каждый спутник со стороны соседей, которая будет мешать лоренцеву сжатию.
Если спутники заменить обычным диском, то в нем при вращении также возникнет сила, которая в итоге и разрушит диск, если скорость вращения будет слишком велика.
Теперь перейдем в СО диска:
Таким образом, в СО диска геометрия изменится.
Как экспериментально отличить лоренцево сокращение линеек, расположенных в СО вращающегося кольца, от обычного растяжения кольца из-за центробежных ускорений?
Тут всё понятно из-за линейной скорости V (V=wR) спутник будет испытывать лоренцево сжатие, которое никак не заметят, находящиеся в нем приборы.
Теперь усложним опыт. Пусть спутников много и они занимают всю окружность орбиты, опять ничего не изменилось, каждый спутник испытывает лоренцево сжатие.
Но теперь соединим спутники пружинами или заменим на орбитальное кольцо. Каждый спутник и сама пружина испытывает сокращение, но при этом их тянет пружина, поэтому возникнет сила, действующая на каждый спутник со стороны соседей, которая будет мешать лоренцеву сжатию.
Если спутники заменить обычным диском, то в нем при вращении также возникнет сила, которая в итоге и разрушит диск, если скорость вращения будет слишком велика.
Теперь перейдем в СО диска:
Представим себе большой плоский диск с центром С, который, по утверждению наблюдателя О, вращается вокруг оси, проходящей через точку С перпендикулярно плоскости диска. Представим себе, что на диске живет другой наблюдатель начало системы отсчета которого находится в точке С, а оси лежат в плоскости диска и направлены вдоль и перпендикулярно
Наблюдатель А считает, что диск находится в состоянии покоя, а наблюдатель О движется по кругу в противоположном направлении Но А отдает себе отчет в том, что он вынужден прикрепить себя к диску, чтобы удержаться на ногах. По его представлению, существует поле силы тяжести, действующее в направлении от С и пропорциональное расстоянию от этой точки. Однако наблюдатель О утверждает, что А движется с постоянной скоростью по окружности с центром в С, поэтому А имеет ускорение, направленное к С и создаваемое его опорой, подобно тому как камень, привязанный к концу веревки и вращающийся по кругу, удерживается на окружности благодаря натяжению веревки.
...
Допустим, что на диске начерчен круг с центром в точке С и что наблюдатель с помощью своей линейки измеряет его диаметр и длину его окружности. Допустим, что по измерениям диаметр оказался в раз больше использованной им линейки. Наблюдатель О согласится с этим результатом, так как в любом радиальном направлении линейка не будет иметь продольной скорости относительно О. Но если наблюдатель расположит свою линейку по касательной к окружности и станет измерять ее длину небольшими отрезками, то линейка, с точки зрения наблюдателя О, будет в этом случае иметь продольную скорость и поэтому, по мнению О, она испытывает сокращение. Наблюдателю О известно, что длина окружности равна произведению на ее диаметр, где число Таким образом, если бы линейка не испытывала сжатия, то она уложилась бы на длине окружности раза. Однако вследствие сокращения длины линейки число отрезков увеличится. Наблюдая, как производит измерение, наблюдатель О обнаружит, что, пользуясь испытавшей сокращение линейкой, этот наблюдатель уложит ее на длине окружности, скажем, 3 300000 раз. Что касается любого счета, то тут оба наблюдателя должны прийти к единому мнению. Для наблюдателя этот результат окажется неожиданным, поскольку он остается в неведении относительно сокращения линейки и будет вынужден прийти к выводу, что отношение длины окружности к ее диаметру уже не равно 3,14159..., а в данном случае составляет 3,3.
...
Итак, мы видим, что в системе наблюдателя А длина окружности не пропорциональна ее диаметру; иными словами, две окружности разного размера не будут подобны друг другу (т. е. будут иметь разную форму). Это означает, что геометрия А не совпадает с геометрией Евклида, и мы считаем, что пространство А — неевклидово.
> Жизнь на вращающемся диске
Таким образом, в СО диска геометрия изменится.
Как экспериментально отличить лоренцево сокращение линеек, расположенных в СО вращающегося кольца, от обычного растяжения кольца из-за центробежных ускорений?


Это сообщение редактировалось 27.09.2021 в 16:31
aФон> Начнем с космического эксперимента
Афон, нафига ты сюда это тащишь?
Если ты, на старости лет, обнаружил детские книжки по ТО, то это совсем не значит, что остальные тоже необразованные неучи, как ты.
И им будет интересно с тобой что-то обсуждать.
Лично я ТО проходил в школе, в восьмом классе, когда примитивная механика.
Со всеми "парадоксами".
Никаких "открытий чудных" ты не совершишь.
Ковыряй свою квадратную Землю и Луну из сыра, это, хотя бы, смешно.
Афон, нафига ты сюда это тащишь?
Если ты, на старости лет, обнаружил детские книжки по ТО, то это совсем не значит, что остальные тоже необразованные неучи, как ты.
И им будет интересно с тобой что-то обсуждать.
Лично я ТО проходил в школе, в восьмом классе, когда примитивная механика.
Со всеми "парадоксами".
Никаких "открытий чудных" ты не совершишь.
Ковыряй свою квадратную Землю и Луну из сыра, это, хотя бы, смешно.


Xan> Лично я ТО проходил в школе, в восьмом классе, когда примитивная механика.
Xan> Со всеми "парадоксами".
Ну и что? Проходил и глубин не понял, таких как Вы - вагон и маленькая тележка.
Xan> Никаких "открытий чудных" ты не совершишь.
Xan> Ковыряй свою квадратную Землю и Луну из сыра, это, хотя бы, смешно.
Если разрезать вращаюшееся кольцо, то проблемы сразу исчезают, зазор (разрез) будет расти с ростом скорости из-за лоренцева сокращения, никаких напряжений в кольцо возникать не будет.
Xan> Со всеми "парадоксами".
Ну и что? Проходил и глубин не понял, таких как Вы - вагон и маленькая тележка.
Xan> Никаких "открытий чудных" ты не совершишь.
Xan> Ковыряй свою квадратную Землю и Луну из сыра, это, хотя бы, смешно.
Если разрезать вращаюшееся кольцо, то проблемы сразу исчезают, зазор (разрез) будет расти с ростом скорости из-за лоренцева сокращения, никаких напряжений в кольцо возникать не будет.


aФон> Таким образом, классики настаивают, что геометрия изменится, а никаких сил не возникнет.
aФон> А что говорит ЭКСПЕРИМЕНТ?
Теория говорит что ускорение эквивалентно гравитации.
А конкретно центробежное ускорение - гравитации с отрицательным знаком.
Т.е. наблюдатель - должен усомниться не в величине пи, а в длине диаметра. Который поменял свой размер вследствие искривления пространства под действием (анти)гравитации.
aФон> А что говорит ЭКСПЕРИМЕНТ?
Теория говорит что ускорение эквивалентно гравитации.
А конкретно центробежное ускорение - гравитации с отрицательным знаком.
Т.е. наблюдатель - должен усомниться не в величине пи, а в длине диаметра. Который поменял свой размер вследствие искривления пространства под действием (анти)гравитации.

aФон> Но теперь соединим спутники пружинами или заменим на орбитальное кольцо. Каждый спутник и сама пружина испытывает сокращение, но при этом их тянет пружина, поэтому возникнет сила, действующая на каждый спутник со стороны соседей, которая будет мешать лоренцеву сжатию.
Будь добр. Изучи, пожалуйста, букварь про квантовую теорию строения твёрдого тела. Пожалуйста. Там есть ответы на твои вопросы.
А потом про теорию относительности. И пойми,что абсолютной и универсальной линейки нет. Какие измерения мы можем делать в нашей системе координат (состоянии наблюдателя), такие и можем. Абсолютной системы координат нет.
Будь добр. Изучи, пожалуйста, букварь про квантовую теорию строения твёрдого тела. Пожалуйста. Там есть ответы на твои вопросы.
А потом про теорию относительности. И пойми,что абсолютной и универсальной линейки нет. Какие измерения мы можем делать в нашей системе координат (состоянии наблюдателя), такие и можем. Абсолютной системы координат нет.


Дем> Теория говорит что ускорение эквивалентно гравитации.
Дем> А конкретно центробежное ускорение - гравитации с отрицательным знаком.
Дем> Т.е. наблюдатель - должен усомниться не в величине пи, а в длине диаметра. Который поменял свой размер вследствие искривления пространства под действием (анти)гравитации.
В этом пассаже осталось не раскрытым появление сил вдоль окружности. Из-за лоренцева сжатия и сопротивлению ему замыканием двух концов кольца (если не замыкать, то и сил не будет), возникнут силы, стремящиеся разорвать это кольцо.
Как нам получить эти силы в описании через гравитацию?
Sandro> Будь добр. Изучи, пожалуйста, букварь про квантовую теорию строения твёрдого тела. Пожалуйста. Там есть ответы на твои вопросы.
Не говорите, что мне делать и я не скажу, куда Вам пойти.
Sandro> А потом про теорию относительности. И пойми,что абсолютной и универсальной линейки нет.
Не повторяйте прописных истин, по теме есть что сказать?
Дем> А конкретно центробежное ускорение - гравитации с отрицательным знаком.
Дем> Т.е. наблюдатель - должен усомниться не в величине пи, а в длине диаметра. Который поменял свой размер вследствие искривления пространства под действием (анти)гравитации.
В этом пассаже осталось не раскрытым появление сил вдоль окружности. Из-за лоренцева сжатия и сопротивлению ему замыканием двух концов кольца (если не замыкать, то и сил не будет), возникнут силы, стремящиеся разорвать это кольцо.
Как нам получить эти силы в описании через гравитацию?
Sandro> Будь добр. Изучи, пожалуйста, букварь про квантовую теорию строения твёрдого тела. Пожалуйста. Там есть ответы на твои вопросы.
Не говорите, что мне делать и я не скажу, куда Вам пойти.
Sandro> А потом про теорию относительности. И пойми,что абсолютной и универсальной линейки нет.
Не повторяйте прописных истин, по теме есть что сказать?


aФон> Проходил и глубин не понял,
Ага, ага!
А ты сейчас почитал популярную литературу и всё внезапно понял.
Гениально.
aФон> Если разрезать вращаюшееся кольцо, то проблемы сразу исчезают, зазор (разрез) будет расти с ростом скорости из-за лоренцева сокращения, никаких напряжений в кольцо возникать не будет.
И что?
Это мне было очевидно ещё в восьмом классе.
aФон> Не говорите, что мне делать и я не скажу, куда Вам пойти.
Не наглей.
Иначе пойдёшь нахер.
Ты здесь клоуном работаешь.
Ага, ага!
А ты сейчас почитал популярную литературу и всё внезапно понял.
Гениально.
aФон> Если разрезать вращаюшееся кольцо, то проблемы сразу исчезают, зазор (разрез) будет расти с ростом скорости из-за лоренцева сокращения, никаких напряжений в кольцо возникать не будет.
И что?
Это мне было очевидно ещё в восьмом классе.
aФон> Не говорите, что мне делать и я не скажу, куда Вам пойти.
Не наглей.
Иначе пойдёшь нахер.
Ты здесь клоуном работаешь.


aФон>> Если разрезать вращаюшееся кольцо, то проблемы сразу исчезают, зазор (разрез) будет расти с ростом скорости из-за лоренцева сокращения, никаких напряжений в кольцо возникать не будет.
Xan> И что?
Xan> Это мне было очевидно ещё в восьмом классе.
Именно это и отрицается классиками, это и есть причина появление темы.
Считается, что из-за искривления пространства полем ускорения, геометрия изменится и длина, измеренная в новой геометрии будет меньше, то есть нет никакого повода для сил.
Прочитайте три странички учебника из первого сообщения.
Xan> И что?
Xan> Это мне было очевидно ещё в восьмом классе.
Именно это и отрицается классиками, это и есть причина появление темы.
Считается, что из-за искривления пространства полем ускорения, геометрия изменится и длина, измеренная в новой геометрии будет меньше, то есть нет никакого повода для сил.
Прочитайте три странички учебника из первого сообщения.


Xan>> Это мне было очевидно ещё в восьмом классе.
aФон> Именно это и отрицается классиками, это и есть причина появление темы.
aФон> Считается, что из-за искривления пространства полем ускорения, геометрия изменится и длина, измеренная в новой геометрии будет меньше, то есть нет никакого повода для сил.
Ты дурак?
А впрочем, о чём это я?
aФон> Именно это и отрицается классиками, это и есть причина появление темы.
aФон> Считается, что из-за искривления пространства полем ускорения, геометрия изменится и длина, измеренная в новой геометрии будет меньше, то есть нет никакого повода для сил.
Ты дурак?
А впрочем, о чём это я?



Sandro> Чисто в рамках самообразования. Я могу узнать, что такое "поле ускорения"?
Можете:
В СО на диске измерят окружность и увидят, что она больше, чем 2пиR (потому что из ИСО видят, что линейки сжались из-за лоренцева сокращения).
Поскольку на диске как бы существует поле гравитации, то там присутствует искривление пространства-времени, а раз так, то и длина окружности не обязана быть равной 2пиR.
Но как объяснить появление сил, стремящихся разорвать диск с позиции СО диска (в которой появилось поле гравитации)?
Важно понимать, что линейка, лежащая на кольце не имеет сил напряжения, а в самом кольце они есть. И вызваны они тем, что за диаметрально-противоположные концы кольца тянет сила «гравитации». Можно ли утверждать, что напряжение созданное этой силой линейно связано с лоренц-сокращением?
Xan> Ты дурак?
Нехороший ты человек, Косой, злой, как собака
«Джентльмены удачи» ― Иди отсюда! Тебе что сказано? Ну-ка иди, давай! ― Нехороший ты человек, Косой, злой, как собака.
Можете:
Под принципом эквивалентности в теории тяготения понимается утверждение, согласно которому поле ускорения в каком-то смысле эквивалентно полю тяготения / В.А.Фок ТЕОРИЯ ПРОСТРАНСТВА, ВРЕМЕНИ И ТЯГОТЕНИЯ /
В СО на диске измерят окружность и увидят, что она больше, чем 2пиR (потому что из ИСО видят, что линейки сжались из-за лоренцева сокращения).
Поскольку на диске как бы существует поле гравитации, то там присутствует искривление пространства-времени, а раз так, то и длина окружности не обязана быть равной 2пиR.
Но как объяснить появление сил, стремящихся разорвать диск с позиции СО диска (в которой появилось поле гравитации)?
Важно понимать, что линейка, лежащая на кольце не имеет сил напряжения, а в самом кольце они есть. И вызваны они тем, что за диаметрально-противоположные концы кольца тянет сила «гравитации». Можно ли утверждать, что напряжение созданное этой силой линейно связано с лоренц-сокращением?
Xan> Ты дурак?
Нехороший ты человек, Косой, злой, как собака
«Джентльмены удачи» ― Иди отсюда! Тебе что сказано? Ну-ка иди, давай! ― Нехороший ты человек, Косой, злой, как собака.


Это сообщение редактировалось 27.09.2021 в 05:38
aФон> Под принципом эквивалентности в теории тяготения понимается утверждение, согласно которому поле ускорения в каком-то смысле эквивалентно полю тяготения
Какая-то жуткая херня написана.
Типа школьной херни: "аксиома принимается на веру, без доказательства" [тут должен быть колокольный звон ].
].
Во времена Ньютона у каждого предмета было две РАЗНЫХ массы.
Гравитационная участвовала в законе притяжения, а инертная в законах Ньютона про ускорение.
Умные люди понимали, что это именно два разных свойства предметов.
Которые ПОЧЕМУ-ТО при измерениях получались всё время одинаковые. Независимо от формы и состава вещества.
А измерений проводилось много, всё более точные, потому что очень хотелось найти разницу и понять, от чего она зависит.
Эйнштейн выбросил эту проблему, приняв в основание своей теории аксиому эквивалентности гравитационной и инертной масс.
И не "в каком-то смысле", б**!
А выбросил две разных массы и ввёл одну единственную.
Аксиомой.
Какая-то жуткая херня написана.
Типа школьной херни: "аксиома принимается на веру, без доказательства" [тут должен быть колокольный звон
 ].
].Во времена Ньютона у каждого предмета было две РАЗНЫХ массы.
Гравитационная участвовала в законе притяжения, а инертная в законах Ньютона про ускорение.
Умные люди понимали, что это именно два разных свойства предметов.
Которые ПОЧЕМУ-ТО при измерениях получались всё время одинаковые. Независимо от формы и состава вещества.
А измерений проводилось много, всё более точные, потому что очень хотелось найти разницу и понять, от чего она зависит.
Эйнштейн выбросил эту проблему, приняв в основание своей теории аксиому эквивалентности гравитационной и инертной масс.
И не "в каком-то смысле", б**!
А выбросил две разных массы и ввёл одну единственную.
Аксиомой.


Не отклоняйтесь от темы. Итак, с точки зрения ИСО, с вращающимся кольцом происходит такие вещи:
1/ Оно растягивается из-за центробежных сил
2/ Растяжение не отражается на отклонении от геометрии плоского пространства
3/ Происходит лоренцево сжатие и это уже делает линейки, лежащие вдоль кольца короче.
4/ Если измерить этими линейками длину окружности, то само выражение длины не дает представление о лоренцевом сжатии линеек, потому что кольцо растягивалось еще и вместе с диаметром.
5/ В силу 4 нужно измерить линейками сначала диаметр, а потом через него выразить длину окружности, в отклонении от 2пиR и сидит лоренцево сжатие линеек.
Теперь смотрим из СО самого кольца
1/ Оно растягивается гравитацией
2/ Сама гравитация искривляет пространство-время, то есть как бы превращает круг в воронку (водоворота), поэтому диаметр не связан с длиной через пи.
Я ничего не упустил?
aФон>> Под принципом эквивалентности в теории тяготения понимается утверждение, согласно которому поле ускорения в каком-то смысле эквивалентно полю тяготения
Xan> Какая-то жуткая херня написана.
Xan> Типа школьной херни: "аксиома принимается на веру, без доказательства" [тут должен быть колокольный звон ].
].
Xan> Эйнштейн выбросил эту проблему, приняв в основание своей теории аксиому эквивалентности гравитационной и инертной масс.
Xan> И не "в каком-то смысле", б**!
Xan> А выбросил две разных массы и ввёл одну единственную.
Xan> Аксиомой.
А что Вам помешало перейти по ссылке и уточнить, что означает фраза, какой контекст подразумевался?
1/ Оно растягивается из-за центробежных сил
2/ Растяжение не отражается на отклонении от геометрии плоского пространства
3/ Происходит лоренцево сжатие и это уже делает линейки, лежащие вдоль кольца короче.
4/ Если измерить этими линейками длину окружности, то само выражение длины не дает представление о лоренцевом сжатии линеек, потому что кольцо растягивалось еще и вместе с диаметром.
5/ В силу 4 нужно измерить линейками сначала диаметр, а потом через него выразить длину окружности, в отклонении от 2пиR и сидит лоренцево сжатие линеек.
Теперь смотрим из СО самого кольца
1/ Оно растягивается гравитацией
2/ Сама гравитация искривляет пространство-время, то есть как бы превращает круг в воронку (водоворота), поэтому диаметр не связан с длиной через пи.
Я ничего не упустил?
aФон>> Под принципом эквивалентности в теории тяготения понимается утверждение, согласно которому поле ускорения в каком-то смысле эквивалентно полю тяготения
Xan> Какая-то жуткая херня написана.
Xan> Типа школьной херни: "аксиома принимается на веру, без доказательства" [тут должен быть колокольный звон
 ].
].Xan> Эйнштейн выбросил эту проблему, приняв в основание своей теории аксиому эквивалентности гравитационной и инертной масс.
Xan> И не "в каком-то смысле", б**!
Xan> А выбросил две разных массы и ввёл одну единственную.
Xan> Аксиомой.
А что Вам помешало перейти по ссылке и уточнить, что означает фраза, какой контекст подразумевался?
Прикреплённые файлы:


Xan> Во времена Ньютона у каждого предмета было две РАЗНЫХ массы.
Xan> Гравитационная участвовала в законе притяжения, а инертная в законах Ньютона про ускорение.
Xan> Умные люди понимали, что это именно два разных свойства предметов.
Xan> Которые ПОЧЕМУ-ТО при измерениях получались всё время одинаковые. Независимо от формы и состава вещества.
Xan> А измерений проводилось много, всё более точные, потому что очень хотелось найти разницу и понять, от чего она зависит.
Xan> Эйнштейн выбросил эту проблему, приняв в основание своей теории аксиому эквивалентности гравитационной и инертной масс.
Это еще Галилей доказал, Эйнштейн сделал нечто большее
Xan> Гравитационная участвовала в законе притяжения, а инертная в законах Ньютона про ускорение.
Xan> Умные люди понимали, что это именно два разных свойства предметов.
Xan> Которые ПОЧЕМУ-ТО при измерениях получались всё время одинаковые. Независимо от формы и состава вещества.
Xan> А измерений проводилось много, всё более точные, потому что очень хотелось найти разницу и понять, от чего она зависит.
Xan> Эйнштейн выбросил эту проблему, приняв в основание своей теории аксиому эквивалентности гравитационной и инертной масс.
Это еще Галилей доказал, Эйнштейн сделал нечто большее
Согласно слабому принципу эквивалентности инерциальная масса равна гравитационной массе и ее можно сократить. Получится, что ускорение, называемое в данном случае ускорением свободного падения, не зависит от массы падающего тела.
Вообще-то это наблюдал еще Галилей, сбрасывая шары разных масс с Пизанской башни. Что же сделал Эйнштейн?
Эйнштейн просто немного обобщил это наблюдение Галилея. Он сказал: смотрите, получается, что мы в принципе не можем отличить инерцию от гравитации.
Известен его знаменитый мысленный эксперимент “человек в лифте”. Пусть герметичный, непрозрачный и хорошо изолированный от окружающей среды лифт с человеком внутри сбрасывают с самолета. Человек при падении будет находиться в состоянии невесомости и не имея возможности посмотреть наружу он не сможет сказать падает ли он на Землю или может быть находится где-то вдали от звезд, в межзвездном космическом пространстве в отсутствии всяких гравитационных сил. Он ведь не ощущает силу гравитации. Это по-сути и называется невесомостью.
Можно рассмотреть другую ситуацию. Этот лифт привязан к ракете, движущейся с ускорением 9.8 м/с2. Человек будет испытывать силу инерции, но опять же не имея возможности посмотреть наружу он может подумать, что лифт просто стоит на поверхности Земли и он испытывает не силу инерции, а гравитационное притяжение Земли. Он опять же никак не может отличить силы инерции от гравитационного поля.
Принцип эквивалентности Эйнштейна гласит, что никакими локальными экспериментами невозможно обнаружить гравитационное поле. Гравитационные эффекты неотличимы от инерциальных сил.
Важным тут является слово «локальными». То есть должны рассматриваться небольшие области пространства. Если падающий на землю лифт имеет значительные размеры, то в нем можно наблюдать неоднородность гравитационного поля, обусловленного тем, что все векторы сил направлены к центру Земли. Векторы же сил при ускоренном движении направлены по направлению движения.
Гравитация неотличима от инерциальных сил в малой области, по сути в точке. Но в 1905 году Эйнштейн своей специальной теорией относительности уже обобщил закон инерции ньютона. И согласно принципу эквивалентности Эйнштейна получается, что гравитационные эффекты в малой области пространства неотличимы от эффектов специальной теории относительности, которая обобщает ньютоновскую механику.
Теория гравитации должна сводиться к специальной теории относительности в малых областях пространства. Он назвал такую теорию гравитации общей теорией относительности.
> Относительность 13 — Принцип эквивалентности Эйнштейна | LightCone


aФон> Вообще-то это наблюдал еще Галилей, сбрасывая шары разных масс с Пизанской башни. Что же сделал Эйнштейн?
aФон> Эйнштейн просто немного обобщил
Я вижу, что физику ты вообще нихера не понимаешь.
Ты даже не способен понять, почему аксиома называется "принцип эквивалентности".
Хотя я всё объяснил.
Предъяви фотку своего диплома.
Что я знал, что у тебя может быть в голове.
На что рассчитывать.
aФон> Эйнштейн просто немного обобщил
Я вижу, что физику ты вообще нихера не понимаешь.
Ты даже не способен понять, почему аксиома называется "принцип эквивалентности".
Хотя я всё объяснил.
Предъяви фотку своего диплома.
Что я знал, что у тебя может быть в голове.
На что рассчитывать.


aФон>> Вообще-то это наблюдал еще Галилей, сбрасывая шары разных масс с Пизанской башни. Что же сделал Эйнштейн?
aФон>> Эйнштейн просто немного обобщил
Xan> Я вижу, что физику ты вообще нихера не понимаешь.
Xan> Ты даже не способен понять, почему аксиома называется "принцип эквивалентности".
У тебя, похоже, различалка перестала работать. Есть сильный принцип эквивалентности, а есть слабый.
Почитай Фока, ссылка выше была, он разжевывает подробнее
aФон>> Эйнштейн просто немного обобщил
Xan> Я вижу, что физику ты вообще нихера не понимаешь.
Xan> Ты даже не способен понять, почему аксиома называется "принцип эквивалентности".
У тебя, похоже, различалка перестала работать. Есть сильный принцип эквивалентности, а есть слабый.
Исторически, принцип относительности был сформулирован Эйнштейном так:
Все явления в гравитационном поле происходят точно так же как в соответствующем поле сил инерции, если совпадают напряжённости этих полей и одинаковы начальные условия для тел системы.
…
Следует различать «слабый принцип эквивалентности» и «сильный принцип эквивалентности». Сильный принцип эквивалентности можно сформулировать так: в каждой точке пространства-времени в произвольном гравитационном поле можно выбрать «локально-инерциальную систему координат», такую, что в достаточно малой окрестности рассматриваемой точки законы природы будут иметь такую же форму, как и в не ускоренных декартовых системах координат, где под «законами природы» подразумевают все законы природы.
Слабый принцип отличается тем, что слова «законы природы» заменяются в нем словами «законы движения свободно падающих частиц». Слабый принцип — это не что иное, как другая формулировка наблюдаемого равенства гравитационной и инертной масс, в то время как сильный принцип сильный принцип представляет собой обобщение наблюдений за влиянием гравитации на любые физические объекты.
> Принцип эквивалентности - это... Что такое Принцип эквивалентности?
Почитай Фока, ссылка выше была, он разжевывает подробнее
Прикреплённые файлы:


Это сообщение редактировалось 27.09.2021 в 19:55
Xan> Хотя я всё объяснил.
Ты объяснил грубо (в первом приближении, для школоты), с потерей тонких деталей и смыслов. Суть эйнштейновского принципа эквивалентности в тождестве ускоренной системы и поля гравитации, именно за это Фок и критикует позицию Эйнштейна, доказывая, что достаточно установленного в опыте закона равенства инертной и гравитационной массы, дескать, предложенный Эйнштейном принцип эквивалентности – это просто выражение гипотезы о римановом пространстве-времени.
Достаточно посмотреть на работы Эйнштейна или на их разбор и сразу ясно, о какой эквивалентности в них речь:
Ты объяснил грубо (в первом приближении, для школоты), с потерей тонких деталей и смыслов. Суть эйнштейновского принципа эквивалентности в тождестве ускоренной системы и поля гравитации, именно за это Фок и критикует позицию Эйнштейна, доказывая, что достаточно установленного в опыте закона равенства инертной и гравитационной массы, дескать, предложенный Эйнштейном принцип эквивалентности – это просто выражение гипотезы о римановом пространстве-времени.
Достаточно посмотреть на работы Эйнштейна или на их разбор и сразу ясно, о какой эквивалентности в них речь:
В работе 1907 г., о которой мы говорили в своем месте, Эйнштейн впервые поставил вопрос о распространении принципа относительности на ускоренные системы отсчета. В связи с этим вопросом Эйнштейн пишет: "Рассмотрим две системы отсчета ∑1 и ∑2. Пусть ∑1 движется с ускорением в направлении своей оси х, и пусть ее ускорение (постоянное во времени) равно γ. Предположим, что ∑2 покоится, но находится в однородном гравитационном поле, которое сообщает всем телам ускорение -γ в направлении оси х.
Как известно, физические законы относительно ∑1 не отличаются от законов, отнесенных к ∑2, это связано с тем, что в гравитационном ноле все тела ускоряются одинаково. Поэтому при современном состоянии наших знаний нет никаких оснований полагать, что системы отсчета ∑1 и ∑2 в каком-либо отношении отличаются друг от друга, и в дальнейшем мы будем предполагать полную физическую равноценность гравитационного поля и соответствующего ускорения системы отсчета". Так впервые появился в науке этот знаменитый принцип, пока в качестве гипотезы.
…
Тем временем Эйнштейн продолжает размышлять над вопросами тяготения. В 1911 г. он опубликовал статью "О влиянии силы тяготения на распространение света". В этой работе Эйнштейн вновь формулирует принцип эквивалентности однородного гравитационного поля и равномерно ускоренной системы отсчета. Рассматривая две системы К и К', из которых первая К' покоится в однородном поле тяжести, направленном вдоль отрицательной оси z, а другая К движется в свободном пространстве вдоль положительной оси z с постоянным ускорением γ, Эйнштейн указывает, что в обеих системах справедливы уравнения движения свободной материальной точки вида
"Для ускоренной системы отсчета К',- пишет Эйнштейн,- это следует прямо из принципа Галилея; для покоящейся же в однородном гравитационном поле системы отсчета К это следует из того опытного факта, что все тела в таком поле ускоряются равномерно и одинаково сильно. Этот опытный факт об одинаковом ускорении падения всех падающих в гравитационном поле тел является одним из наиболее общих фактов, установленных нами из наблюдений; несмотря на это, закон этот не нашел еще отражения в основах нашей физической картины мира"
Прошло триста лет с тех пор, как Галилей прямым опытом опроверг утверждение Аристотеля о зависимости скорости падения тяжелых тел от их массы. Галилей установил, что в отсутствии сопротивления воздуха все тела падают одинаково. С этого наблюдения Галилея датируется новая физика - физика опыта и математической теории. Наблюдение Галилея о равенстве гравитационной и инертной масс неоднократно проверялось многими физиками, начиная с Ньютона. В 1890 г. венгерский физик Лоранд Этвеш опытом с крутильными весами доказал равенство инертной и тяжелой масс с точностью до 1/2*10-7. В 1909 г. Д. Пекар и Э. Фекете подтвердили результат Этвеша с точностью до 10-8.
Таким образом, к моменту появления статьи Эйнштейна равенство инертной и гравитационной масс было одним из наиболее точно установленных фактов физики. Из этого факта и вытекает отмеченная Эйнштейном эквивалентность систем отсчета К и К' в отношении описания механических явлений. Но в работе 1911 г. Эйнштейн идет дальше и постулирует эквивалентность обеих систем для любых физических явлений. "Однако,- пишет Эйнштейн,- представление наше будет достаточно глубоким только в том случае, если системы К и К' окажутся равноценными относительно всех физических явлений, т. е. если законы природы по отношению к системе К полностью совпадут с законами природы по отношению к системе К'. Приняв это, мы получаем принцип, имеющий большое эвристическое значение, если он действительно справедлив"".
В работе 1912 г. "Скорость света и статическое гравитационное поле" впервые появляется термин "принцип эквивалентности" для "гипотезы о физической эквивалентности ускоренной системы координат полю тяжести".
> Принцип эквивалентности [1971 Кудрявцев П.С. - История физики. Том 3. От открытия квант до квантовой механики]


 Реклама Google — средство выживания форумов :)
Реклама Google — средство выживания форумов :)
Пусть у нас есть сильно гравитирующий объект, а в его поле проводят опыт Галилея.
Бросают два шара одинакового объема, один из камня, а второй резиновый.
На определенном расстоянии каменный шар разрушается приливными силами, а резиновый спокойно долетает до конца.
Какой принцип эквивалентности тут нарушился?
Бросают два шара одинакового объема, один из камня, а второй резиновый.
На определенном расстоянии каменный шар разрушается приливными силами, а резиновый спокойно долетает до конца.
Какой принцип эквивалентности тут нарушился?


Copyright © Balancer 1997..2022
Создано 26.09.2021
Связь с владельцами и администрацией сайта: anonisimov@gmail.com, rwasp1957@yandex.ru и admin@balancer.ru.
Создано 26.09.2021
Связь с владельцами и администрацией сайта: anonisimov@gmail.com, rwasp1957@yandex.ru и admin@balancer.ru.
 aФон
aФон

 инфо
инфо инструменты
инструменты Xan
Xan

 Дем
Дем


 aФон
aФон

 aФон
aФон

 aФон
aФон
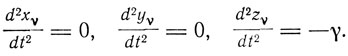
 aФон
aФон
