Реклама Google — средство выживания форумов :)
Реклама Google — средство выживания форумов :)
-
![[image]](https://www.balancer.ru/cache/sites/w/w/www.afterwork.com.ua/wp-content/uploads/2011/03/128x128-crop/launcher_a2.jpg)
Обыкновенные водяные ракеты из пластиковых бутылок
Теги:
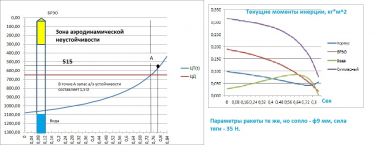
PopovIgor> Для примера просчитана одноступенчатая ракета с конкретными данными.
Полезнейшие графики !
Особенно второй.
До настоящего времени нигде похожих расчетов не публиковалось.
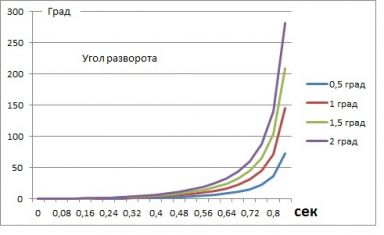
Ко второму графику логично приложить доходчивый рисунок:
длинная ракета изогнулась дугой, видно, что направление вектора тяги (ось сопла) не совпадает с направлением на центр масс.
Полезнейшие графики !
Особенно второй.
До настоящего времени нигде похожих расчетов не публиковалось.
Ко второму графику логично приложить доходчивый рисунок:
длинная ракета изогнулась дугой, видно, что направление вектора тяги (ось сопла) не совпадает с направлением на центр масс.


Ckona> Полезнейшие графики !
Ckona> Особенно второй.
Ckona> До настоящего времени нигде похожих расчетов не публиковалось.
Есть и расчетные формулы с текущими значениями, не знаю, нужны -не нужны.
Видно, что наибольший момент импульса в самом конце водяной тяги. Как на практике, соответствуют ли значения разворота, хоть примерно?
С бОльшими углами отклонения вектора тяги ракету крутит очень значительно.
Правда и сила тяги забита 300 Н.
Ckona> Особенно второй.
Ckona> До настоящего времени нигде похожих расчетов не публиковалось.
Есть и расчетные формулы с текущими значениями, не знаю, нужны -не нужны.
Видно, что наибольший момент импульса в самом конце водяной тяги. Как на практике, соответствуют ли значения разворота, хоть примерно?
С бОльшими углами отклонения вектора тяги ракету крутит очень значительно.
Правда и сила тяги забита 300 Н.


PopovIgor>> Правда и сила тяги забита 300 Н.
Ckona> Нужна вторая серия графиков, для 9-мм сопла.
Ckona> С тягой 35 Н.
Характер кривых такой же. Значения отличаются.
На графике разворота видно, что ощутимый разворот с соплом 9 мм -35 Н начинается раньше, чем с соплом 20 мм -300 Н и углы больше.
Почему?
Чем больше сопло (соответственно сила тяги), тем ракета относительно стабильнее.
Ckona> Нужна вторая серия графиков, для 9-мм сопла.
Ckona> С тягой 35 Н.
Характер кривых такой же. Значения отличаются.
На графике разворота видно, что ощутимый разворот с соплом 9 мм -35 Н начинается раньше, чем с соплом 20 мм -300 Н и углы больше.
Почему?
Чем больше сопло (соответственно сила тяги), тем ракета относительно стабильнее.
Прикреплённые файлы:


Это сообщение редактировалось 29.10.2012 в 22:16
PopovIgor> Почему?
PopovIgor> Чем больше сопло (соответственно сила тяги), тем ракета относительно стабильнее.
Поворачивает не момент, а импульс.
Чем дОльше работает перекошенное сопло, тем быстрее оно раскрутит ракету.
Угол - это двойной интеграл от момента силы.
К тому же у тебя вроде бы центр давления рассчитан без стабилизатора.
PopovIgor> Чем больше сопло (соответственно сила тяги), тем ракета относительно стабильнее.
Поворачивает не момент, а импульс.
Чем дОльше работает перекошенное сопло, тем быстрее оно раскрутит ракету.
Угол - это двойной интеграл от момента силы.
К тому же у тебя вроде бы центр давления рассчитан без стабилизатора.


Ckona> К тому же у тебя вроде бы центр давления рассчитан без стабилизатора.
Да, без него.
На всех графиках угла разворота все значения надо уменьшить вдвое.
Забыл на двойку поделить.
После прохождения ЦТ через ЦД сопротивление приложенное к ЦД препятствует нарастанию разворота. До этого наоборот способствовало.
Не от этого ли тоже и "виляние" после воды?
На графике изменения момента инерции корпуса (пустотелый цилиндр) виден минимум (график 2). Эта точка точна соответствует середине длины корпуса (график 1).
Да, без него.
На всех графиках угла разворота все значения надо уменьшить вдвое.
Забыл на двойку поделить.

После прохождения ЦТ через ЦД сопротивление приложенное к ЦД препятствует нарастанию разворота. До этого наоборот способствовало.
Не от этого ли тоже и "виляние" после воды?
На графике изменения момента инерции корпуса (пустотелый цилиндр) виден минимум (график 2). Эта точка точна соответствует середине длины корпуса (график 1).


Это сообщение редактировалось 29.10.2012 в 19:48
Ckona> Твои разделители ступеней на воздушных шариках работают как часы.
Ckona> Представляю, сколько усердия ты тратишь на исполнение...
Честно признаюсь, усилий я трачу совсем немного, мне просто некогда заниматься ракетами, максимум 1,5часа в день! Узлов соединения у меня 4 шт, причем 2 из первой серии, правда их немного модернизировал, но все работают нормально. В качестве смазки сопел применяю «TEST», моющая паста или густой гель зеленого цвета. Сделал открытие – наклоняешь ступень горизонтально, заправляешь водой, проверяешь уровень воды, а далее сопло залепляешь пастой, и можно вставлять в узел не боясь, что вода выльется. Подаешь давление, паста растворяется, получается мыльный раствор!
График для второго неудачного старта, при первом старте ракета ушла за 100м, но тогда высотомер не стоял. Убедился, что высотомер показывает правильно, ох уж умный и прозорливый у нас Serge77!

Ckona> Представляю, сколько усердия ты тратишь на исполнение...
Честно признаюсь, усилий я трачу совсем немного, мне просто некогда заниматься ракетами, максимум 1,5часа в день! Узлов соединения у меня 4 шт, причем 2 из первой серии, правда их немного модернизировал, но все работают нормально. В качестве смазки сопел применяю «TEST», моющая паста или густой гель зеленого цвета. Сделал открытие – наклоняешь ступень горизонтально, заправляешь водой, проверяешь уровень воды, а далее сопло залепляешь пастой, и можно вставлять в узел не боясь, что вода выльется. Подаешь давление, паста растворяется, получается мыльный раствор!
График для второго неудачного старта, при первом старте ракета ушла за 100м, но тогда высотомер не стоял. Убедился, что высотомер показывает правильно, ох уж умный и прозорливый у нас Serge77!



...
Gematogen> С точки зрения того, что на первой ступени желательна стабилизация - согласен.
....
Gematogen> Лучше бороться с причинами отклонения.
Gematogen> Кстати, Алексей именно по этому пути и идет.
Gematogen> А еще я подозреваю, что для эффективного использования многоступенчатой схемы каждая ступень должна быть в разы (4 - 6) тяжелее (мощнее) совокупности последующих ступеней.
...
Gematogen> Но я могу и серьезно ошибаться
Сейчас проверил технологию изготовления клееного стабилизатора из пластика бутылок. Клей использую MAKROFLEX MF990. Получаются идеальные плоскости. При сшивании подобного качества добиться трудно, да и шить противно! Клей держит очень хорошо, посмотрим, отлетит можно приклеить заново. Изготовил за 1,5часа стабилизатор 1-й ступени. Недостаток технологии – форма и площадь крыла зависит от площади заготовки.
Безусловно, при заправленной ракете толк от стабилизатора маленький, но есть еще пневматическая фаза, по крайней мере, стабилизаторы прекратят вращение. Посмотрим на положение дел на практике!
Конечно, должна быть определенная энергетическая иерархия ступеней, но это цепь последовательная, где каждая ступень вносит посильный вклад в общее дело, поэтому допустимы вольности.
С причинами отклонения бороться пока дело бесперспективное. Алексей, безусловно, идет, но я очень сомневаюсь, что в ту сторону! Мы если и пойдем, то другим путем!
Gematogen> С точки зрения того, что на первой ступени желательна стабилизация - согласен.
....
Gematogen> Лучше бороться с причинами отклонения.
Gematogen> Кстати, Алексей именно по этому пути и идет.
Gematogen> А еще я подозреваю, что для эффективного использования многоступенчатой схемы каждая ступень должна быть в разы (4 - 6) тяжелее (мощнее) совокупности последующих ступеней.
...
Gematogen> Но я могу и серьезно ошибаться

Сейчас проверил технологию изготовления клееного стабилизатора из пластика бутылок. Клей использую MAKROFLEX MF990. Получаются идеальные плоскости. При сшивании подобного качества добиться трудно, да и шить противно! Клей держит очень хорошо, посмотрим, отлетит можно приклеить заново. Изготовил за 1,5часа стабилизатор 1-й ступени. Недостаток технологии – форма и площадь крыла зависит от площади заготовки.
Безусловно, при заправленной ракете толк от стабилизатора маленький, но есть еще пневматическая фаза, по крайней мере, стабилизаторы прекратят вращение. Посмотрим на положение дел на практике!
Конечно, должна быть определенная энергетическая иерархия ступеней, но это цепь последовательная, где каждая ступень вносит посильный вклад в общее дело, поэтому допустимы вольности.
С причинами отклонения бороться пока дело бесперспективное. Алексей, безусловно, идет, но я очень сомневаюсь, что в ту сторону! Мы если и пойдем, то другим путем!



Брат-2> С причинами отклонения бороться пока дело бесперспективное. Алексей, безусловно, идет, но я очень сомневаюсь, что в ту сторону!
Хорошее "спортивное" начало.
Есть сильный резерв по аэродинамической стабильности - смещение перьев стабилизатора назад. Возможен также переход на решетчатые стабилизаторы или их бутылкоориентированный эквивалент.
Я пока готовлю материалы (и решения) по увеличению жесткости состыкованного планера.
Хорошее "спортивное" начало.
Есть сильный резерв по аэродинамической стабильности - смещение перьев стабилизатора назад. Возможен также переход на решетчатые стабилизаторы или их бутылкоориентированный эквивалент.
Я пока готовлю материалы (и решения) по увеличению жесткости состыкованного планера.


Это сообщение редактировалось 29.10.2012 в 23:52
PopovIgor>> Чем больше сопло (соответственно сила тяги), тем ракета относительно стабильнее.
Ckona> Поворачивает не момент, а импульс.
Ckona> Чем дОльше работает перекошенное сопло, тем быстрее оно раскрутит ракету.
Ckona> Угол - это двойной интеграл от момента силы.
Поправил данные, соединил вместе, сетка по Z одинакова, чтобы легче сравнивать.
Для наглядности еще добавил график скорости на этапе истечения воды этой же ракеты, но с разными соплами. Данные по скорости из программы Gematogen'а.
Ckona> Поворачивает не момент, а импульс.
Ckona> Чем дОльше работает перекошенное сопло, тем быстрее оно раскрутит ракету.
Ckona> Угол - это двойной интеграл от момента силы.
Поправил данные, соединил вместе, сетка по Z одинакова, чтобы легче сравнивать.
Для наглядности еще добавил график скорости на этапе истечения воды этой же ракеты, но с разными соплами. Данные по скорости из программы Gematogen'а.
Прикреплённые файлы:


Это сообщение редактировалось 30.10.2012 в 08:36
Ckona> Есть сильный резерв по аэродинамической стабильности - смещение перьев стабилизатора назад.
Истину глаголишь!
Я давно перешел на кольцевые стабилизаторы с сильным смещением назад. Но твои ракеты сложнее и тяжелее.
Попробуй прикинуть сначала размеры и вынос стабилизатора для придания связке аэродинамической устойчивости.
Также нужно помнить, что ракету поворачивает составляющая тяги, а стабилизирует сила сопротивления воздуха. При низких скоростях она ничтожна, а сила тяги - максимальная.
Я продолжаю считать, что стабилизаторы для первой ступени твоей связки практически не сыграют своей роли. Только массу зря увеличишь.
Кроме того потребуется переделка стартового стола.
Попробуй лучше хорошую внешнюю направляющую и средства контроля прямизны ракеты и вертикальности установки.
Даже идеальная ракета при наклонной установке будет заваливаться.
Истину глаголишь!

Я давно перешел на кольцевые стабилизаторы с сильным смещением назад. Но твои ракеты сложнее и тяжелее.
Попробуй прикинуть сначала размеры и вынос стабилизатора для придания связке аэродинамической устойчивости.
Также нужно помнить, что ракету поворачивает составляющая тяги, а стабилизирует сила сопротивления воздуха. При низких скоростях она ничтожна, а сила тяги - максимальная.
Я продолжаю считать, что стабилизаторы для первой ступени твоей связки практически не сыграют своей роли. Только массу зря увеличишь.
Кроме того потребуется переделка стартового стола.
Попробуй лучше хорошую внешнюю направляющую и средства контроля прямизны ракеты и вертикальности установки.
Даже идеальная ракета при наклонной установке будет заваливаться.


Ckona>> Чем дОльше работает перекошенное сопло, тем быстрее оно раскрутит ракету.
SashaPro> Чем дольше работает перекошенное сопло, тем на больший угол будет повёрнута ракета?
SashaPro> Чем короче (быстрее) работает перекошенное сопло, тем быстрее оно раскрутит ракету.
Словами "быстрее оно раскрутит" я обозначил "угол поворота ракеты к моменту завершения воздействия перекошенного сопла".
Сопел два. С тягой 300 Н и с тягой 35 Н.
Угол перекоса одинаковый, ракеты одинаковые, плечо "от перекоса" одинаковое.
Сопло-300 работает 0,1 секунды при среднем моменте инерции ракеты J(300)= 0,5.
Сопло-35 работает 0,8 секунды при среднем моменте инерции ракеты J(35) = 0,7.
Попробую подсчитать...
SashaPro> Чем дольше работает перекошенное сопло, тем на больший угол будет повёрнута ракета?
SashaPro> Чем короче (быстрее) работает перекошенное сопло, тем быстрее оно раскрутит ракету.
Словами "быстрее оно раскрутит" я обозначил "угол поворота ракеты к моменту завершения воздействия перекошенного сопла".
Сопел два. С тягой 300 Н и с тягой 35 Н.
Угол перекоса одинаковый, ракеты одинаковые, плечо "от перекоса" одинаковое.
Сопло-300 работает 0,1 секунды при среднем моменте инерции ракеты J(300)= 0,5.
Сопло-35 работает 0,8 секунды при среднем моменте инерции ракеты J(35) = 0,7.
Попробую подсчитать...


Ckona> Попробую подсчитать...
Так Игорь выложил графики именно для сравнения этих случаев...
Так Игорь выложил графики именно для сравнения этих случаев...


Ckona>> Попробую подсчитать...
Gematogen> Так Игорь выложил графики именно для сравнения этих случаев...
Момент инерции одной и той же системы не может быть разным, если момент инерции данной системы изменяется по одному и тому же закону (сценарию) - истечение одного и того же объема воды.
Единственное, это скорость изменения момента инерции разная. Но средние значения будут всегда одинаковые.
Угловое ускорение прямо пропорционально F*Sin(a), где а - одинаковый угол перекоса. ( e=F*X/J )
ЦM меняет свое положение абсолютно одинаково независимо от сопла, но быстрее или медленнее. Точно так же одинаково меняется плечо X приложения силы F*Sin(a).
Угол же поворота прямо пропорционален угловому ускорению и квадрату времени действия силы F.
В итоге:
с соплом 20 - 300*0,12=3
с сопло 9 - 35*0,82=22,4
Отсюда видно, что во втором случае поворот, как ни странно, будет больше.
Gematogen> Так Игорь выложил графики именно для сравнения этих случаев...
Момент инерции одной и той же системы не может быть разным, если момент инерции данной системы изменяется по одному и тому же закону (сценарию) - истечение одного и того же объема воды.
Единственное, это скорость изменения момента инерции разная. Но средние значения будут всегда одинаковые.
Угловое ускорение прямо пропорционально F*Sin(a), где а - одинаковый угол перекоса. ( e=F*X/J )
ЦM меняет свое положение абсолютно одинаково независимо от сопла, но быстрее или медленнее. Точно так же одинаково меняется плечо X приложения силы F*Sin(a).
Угол же поворота прямо пропорционален угловому ускорению и квадрату времени действия силы F.
В итоге:
с соплом 20 - 300*0,12=3
с сопло 9 - 35*0,82=22,4
Отсюда видно, что во втором случае поворот, как ни странно, будет больше.


Это сообщение редактировалось 30.10.2012 в 13:36
PopovIgor> Отсюда видно, что во втором случае поворот, как ни странно, будет больше.
Для просчитанного примера
сопло 9 - 35*0,842= 24,7
сопло 20 - 300*0,172= 8,67
24,7/8,67 = 2,85, что и видно на графиках углов поворота.
Значения углов отличаются почти в три раза.
Для просчитанного примера
сопло 9 - 35*0,842= 24,7
сопло 20 - 300*0,172= 8,67
24,7/8,67 = 2,85, что и видно на графиках углов поворота.
Значения углов отличаются почти в три раза.


Ckona> Есть сильный резерв по аэродинамической стабильности - смещение перьев стабилизатора назад.
Пока проверю показанный вариант. Погода пока у нас теплая, летать еще можно, причем в комфортных условиях. Выносить стабилизаторы весьма затруднительно, так можно и вид ракеты потерять. Мне еще необходимо проверить поведение клееных стабилизаторов, они установлены на 1-й ступени, если испытание выдержат нормально, то они претендуют стать идеальными крыльями для стабилизатора водяных ракет!
Пока проверю показанный вариант. Погода пока у нас теплая, летать еще можно, причем в комфортных условиях. Выносить стабилизаторы весьма затруднительно, так можно и вид ракеты потерять. Мне еще необходимо проверить поведение клееных стабилизаторов, они установлены на 1-й ступени, если испытание выдержат нормально, то они претендуют стать идеальными крыльями для стабилизатора водяных ракет!
Прикреплённые файлы:


Брат-2>> проверю показанный вариант.
Ckona> Площадь малая. Будет хорошо - с возможностью наращивания.
Ckona> Посмотри ЗРК С-75. Пропорции можно смело "козлить".
Алексей! Указанная тобой ракета мне очень нравится. Нельзя исключить, что мы со временем перейдем на производство копий, но пока к этому шагу не готов. Так как раньше я вообще не использовал стабилизатор на 1-й ступени, то хочу посмотреть результат с тем, что получилось. Площадь плоскостей стабилизатора обусловлена размерами заготовки.
Ckona> Площадь малая. Будет хорошо - с возможностью наращивания.
Ckona> Посмотри ЗРК С-75. Пропорции можно смело "козлить".
Алексей! Указанная тобой ракета мне очень нравится. Нельзя исключить, что мы со временем перейдем на производство копий, но пока к этому шагу не готов. Так как раньше я вообще не использовал стабилизатор на 1-й ступени, то хочу посмотреть результат с тем, что получилось. Площадь плоскостей стабилизатора обусловлена размерами заготовки.


Это сообщение редактировалось 01.11.2012 в 19:16
Брат-2> Нельзя исключить, что мы со временем перейдем на производство копий
Брат-2 !
Открою тебе одну сокровенную тайну.
У нас продают воду в бутылках объемом 2,6 литра сферической формы а-ля футбольный мяч.
Весит она 84 грамма, и толщина стенок 0,64 мм. С такими стенками не страшно и 10 атмосфер !
К сожалению, горлышко диаметром 42 мм и я никак не придумаю, как его заткнуть.
Штатная крышка спокойно выдерживает 3 атмосферы и раздувается как Луна.
Тс-с-с ! (копия Н1-Л3)
Брат-2 !
Открою тебе одну сокровенную тайну.
У нас продают воду в бутылках объемом 2,6 литра сферической формы а-ля футбольный мяч.
Весит она 84 грамма, и толщина стенок 0,64 мм. С такими стенками не страшно и 10 атмосфер !
К сожалению, горлышко диаметром 42 мм и я никак не придумаю, как его заткнуть.
Штатная крышка спокойно выдерживает 3 атмосферы и раздувается как Луна.
Тс-с-с ! (копия Н1-Л3)
Прикреплённые файлы:


...
Ckona> Открою тебе одну сокровенную тайну.
...
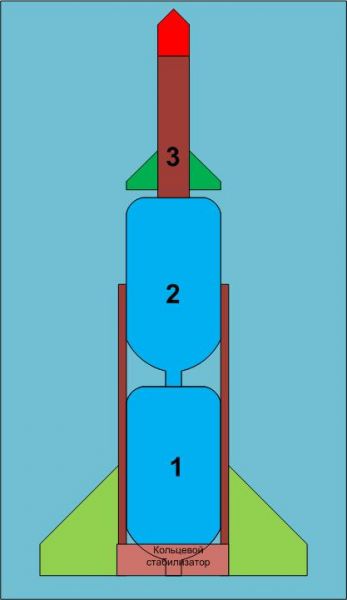
В целях повышения вертикальной устойчивости многоступенчатых ракет в голову пришла компоновка, показанная на фото. При экспериментальном запуске 3-х ступенчатой ракеты было однозначно видно, что проблемы с устойчивостью начались после старта 2-й ступени. 2 ступень имеет объем 5литров, сопло 9мм, поэтому ступень относительно долго работает в активном режиме и, следовательно, жизненно важно обеспечить аэродинамическую устойчивость. Показанная ранее компоновка 1-вых двух ступеней, в которой имеются стабилизаторы на обеих ступенях, может не обеспечить устойчивый вертикальный старт. Подобная ракета будет испытана, но вероятно будет реализована и показанная схема. При последовательной компоновке ступеней важно иметь ступени наименьшей высоты, следовательно, наиболее целесообразно использовать пивные бутылки объемом 5литров. В предлагаемой схеме нет футуристических фантазий. Несущие балки-трубки изготавливаются из пластика бутылок. Технология изготовления подобных трубок освоена как Алексеем, так и мной. Я плотно наматываю пластик бутылки на пластмассовую водопроводную трубу. Обматываю скотчем. Опускаю в горячую воду. Дополнительно пластик можно проклеить. Конец балок, в районе крепления плоскостей стабилизатора скрепляется кольцевой гильзой, что повышает как жесткость, так и общую поверхность стабилизатора. Плоскости стабилизатора изготавливаются из ПЭТ пластика склейкой, впрочем, в ответственных, наиболее нагруженных местах, возможна дополнительная прошивка леской. Схема обеспечивает значительный вынос стабилизатора назад (при старте 2-й ступени), повышает жесткость стыковки ступеней, сохраняется естественный вид стартующей ракеты!
Ckona> Открою тебе одну сокровенную тайну.
...
В целях повышения вертикальной устойчивости многоступенчатых ракет в голову пришла компоновка, показанная на фото. При экспериментальном запуске 3-х ступенчатой ракеты было однозначно видно, что проблемы с устойчивостью начались после старта 2-й ступени. 2 ступень имеет объем 5литров, сопло 9мм, поэтому ступень относительно долго работает в активном режиме и, следовательно, жизненно важно обеспечить аэродинамическую устойчивость. Показанная ранее компоновка 1-вых двух ступеней, в которой имеются стабилизаторы на обеих ступенях, может не обеспечить устойчивый вертикальный старт. Подобная ракета будет испытана, но вероятно будет реализована и показанная схема. При последовательной компоновке ступеней важно иметь ступени наименьшей высоты, следовательно, наиболее целесообразно использовать пивные бутылки объемом 5литров. В предлагаемой схеме нет футуристических фантазий. Несущие балки-трубки изготавливаются из пластика бутылок. Технология изготовления подобных трубок освоена как Алексеем, так и мной. Я плотно наматываю пластик бутылки на пластмассовую водопроводную трубу. Обматываю скотчем. Опускаю в горячую воду. Дополнительно пластик можно проклеить. Конец балок, в районе крепления плоскостей стабилизатора скрепляется кольцевой гильзой, что повышает как жесткость, так и общую поверхность стабилизатора. Плоскости стабилизатора изготавливаются из ПЭТ пластика склейкой, впрочем, в ответственных, наиболее нагруженных местах, возможна дополнительная прошивка леской. Схема обеспечивает значительный вынос стабилизатора назад (при старте 2-й ступени), повышает жесткость стыковки ступеней, сохраняется естественный вид стартующей ракеты!
Прикреплённые файлы:


Брат-2> вероятно будет реализована и показанная схема.
Очень интересно и практично !
Для упрочения несущих трубок я использовал не клей, а заклепки (так быстрее).
Есть некоторое сомнение в гарантированном выталкивании первой ступени - без заклинивания.
Ну так можно вверху еще одно кольцо добавить, чтобы на начальной стадии "выталкивания" верхушка не проскочила вбок между трубками.
Очень интересно и практично !
Для упрочения несущих трубок я использовал не клей, а заклепки (так быстрее).
Есть некоторое сомнение в гарантированном выталкивании первой ступени - без заклинивания.
Ну так можно вверху еще одно кольцо добавить, чтобы на начальной стадии "выталкивания" верхушка не проскочила вбок между трубками.


...
Ckona> Для упрочения несущих трубок я использовал не клей, а заклепки (так быстрее).
Ckona> Есть некоторое сомнение в гарантированном выталкивании первой ступени - без заклинивания.
Ckona> Ну так можно вверху еще одно кольцо добавить, чтобы на начальной стадии "выталкивания" верхушка не проскочила вбок между трубками.
Алексей! Твое сомнение понятно, не исключаю, что я воспользуюсь твоим советом. Идея пока находится на стадии проработки, вернее, на стадии созревания в режиме автопилота. Если удастся добиться приемлемой жесткости несущих балок без заднего кольца, то подобную схему можно использовать и с твоим бустером, о чем собственно я и размышляю! Бустер твоей конструкции у меня ждет своего часа, но, у меня тоже есть сомнения по его эксплуатации. При неудачном старте я набухал в бустер 4,7 литра воды + переборщил как во 2-ю, так и в 3-ю ступень. В результате ракета для 23мм сопла оказалась перетяжеленной. Думаю, что для наших сопел, а именно 23 и 9 мм есть предельная максимальная масса, когда сохраняется приемлемая устойчивость. Вернее не масса конечно, а минимальное ускорение. Кроме того, в проблеме инерционной устойчивости не последнюю роль играет время работы двигателя. То есть я не уверенно, но считаю, что полный объем в 20л, при рациональном объеме воды слишком велик для сопла 23мм. Я могу увеличить диаметр сопла, ведь у моей бутылки базовое сопло в районе 32мм (не измерял), но тогда может не хватить диаметра воздуховодов, в целом – это только темные мысли!
Ckona> Для упрочения несущих трубок я использовал не клей, а заклепки (так быстрее).
Ckona> Есть некоторое сомнение в гарантированном выталкивании первой ступени - без заклинивания.
Ckona> Ну так можно вверху еще одно кольцо добавить, чтобы на начальной стадии "выталкивания" верхушка не проскочила вбок между трубками.
Алексей! Твое сомнение понятно, не исключаю, что я воспользуюсь твоим советом. Идея пока находится на стадии проработки, вернее, на стадии созревания в режиме автопилота. Если удастся добиться приемлемой жесткости несущих балок без заднего кольца, то подобную схему можно использовать и с твоим бустером, о чем собственно я и размышляю! Бустер твоей конструкции у меня ждет своего часа, но, у меня тоже есть сомнения по его эксплуатации. При неудачном старте я набухал в бустер 4,7 литра воды + переборщил как во 2-ю, так и в 3-ю ступень. В результате ракета для 23мм сопла оказалась перетяжеленной. Думаю, что для наших сопел, а именно 23 и 9 мм есть предельная максимальная масса, когда сохраняется приемлемая устойчивость. Вернее не масса конечно, а минимальное ускорение. Кроме того, в проблеме инерционной устойчивости не последнюю роль играет время работы двигателя. То есть я не уверенно, но считаю, что полный объем в 20л, при рациональном объеме воды слишком велик для сопла 23мм. Я могу увеличить диаметр сопла, ведь у моей бутылки базовое сопло в районе 32мм (не измерял), но тогда может не хватить диаметра воздуховодов, в целом – это только темные мысли!



Брат-2> набухал в бустер 4,7 литра воды
Примерно с такой заправкой и летает нынешняя версия моего бутылколета.
Объем 20 литров завышен, боковушки вместо 2,5 л можно спокойно уменьшить до 2,0 л.
Тут я руководствовался стремлением выжать побольше на этапе водной тяги - избыточность воздуха снижает эффект адиабатического охлаждения и падения давления.
Воздцшной тяги у такой разгонной ступени быть не должно - все теряется в трубочках.
Хочу тебя порадовать: в планах на зиму изготовление пневматического выбрасывателя парашюта по твоим материалам. Бутылочек маленьких уже набралось достаточно, в том числе абсолютно круглые поллитровые, для продажи святой воды в церквях. У них донышко толщиной 2,5 мм, держит резьбу М5.
Посмотри на эти чертежи, я их перенес на свой сайт по ссылке Гематогена. Нет ли на них твоего 32-мм горлышка ?
Примерно с такой заправкой и летает нынешняя версия моего бутылколета.
Объем 20 литров завышен, боковушки вместо 2,5 л можно спокойно уменьшить до 2,0 л.
Тут я руководствовался стремлением выжать побольше на этапе водной тяги - избыточность воздуха снижает эффект адиабатического охлаждения и падения давления.
Воздцшной тяги у такой разгонной ступени быть не должно - все теряется в трубочках.
Хочу тебя порадовать: в планах на зиму изготовление пневматического выбрасывателя парашюта по твоим материалам. Бутылочек маленьких уже набралось достаточно, в том числе абсолютно круглые поллитровые, для продажи святой воды в церквях. У них донышко толщиной 2,5 мм, держит резьбу М5.
Посмотри на эти чертежи, я их перенес на свой сайт по ссылке Гематогена. Нет ли на них твоего 32-мм горлышка ?


 Реклама Google — средство выживания форумов :)
Реклама Google — средство выживания форумов :)
В связи со своей старой ошибкой в алгоритме подсчета в таблице углов разворота (тек. уск. умножал на тек. время и суммировал) их значения получились необоснованно завышенными. Надо было тек. ускорение умножать на step t и суммировать нарастающим итогом.
Посыпав голову пеплом, сейчас все исправил и выкладываю результаты. Параметры примера ракеты те же.
а). Сопло 9 мм Тяга 60Н Время ист. - 0,84 сек
б). Сопло 20 мм Тяга 300Н Время ист. - 0,17 сек.
Допускаю, что не всем это интересно и нужно , но тем не менее
Разворот ракеты при том же перекосе сопла продолжится и на пневмовыхлопе.
Однако, хотя момент инерции системы и минимален, незначительно.
Пример для той же ракеты с соплом 9 мм - средняя тяга 60Н .
На воде с перекосом вектора силы тяги в 5 град ракету развернет на 12 град. за 0,84 сек.
После этого ее дополнительно развернет на пневмовыхлопе на 1,5 град за 1,4 сек.
Итого перед выходом в инерциальный полет полный разворот на активном участке составит 13,5 град. за 2,24 сек. Данные силы тяги на пневмовыхлопе взяты из программы Gematogen'а.
Хочу отметить также, что в конце воды (при t=0,72 сек) ЦТ ракеты переходит ЦД и ракета становится аэродинамически устойчивой.
Дальнейшему развороту от перекоса препятствует сила аэродинамического сопротивления. В то время как до этого, эта сила наоборот помогала еще больше разворачивать ракету.
Еще раз отмечу, что данная методика позволяет рассчитывать разворот ракеты в зависимости от перекоса сопла на активном участке и для ракет с любым типом двигателя. Разницы никакой.
Посыпав голову пеплом, сейчас все исправил и выкладываю результаты. Параметры примера ракеты те же.
а). Сопло 9 мм Тяга 60Н Время ист. - 0,84 сек
б). Сопло 20 мм Тяга 300Н Время ист. - 0,17 сек.
Допускаю, что не всем это интересно и нужно , но тем не менее

Разворот ракеты при том же перекосе сопла продолжится и на пневмовыхлопе.
Однако, хотя момент инерции системы и минимален, незначительно.
Пример для той же ракеты с соплом 9 мм - средняя тяга 60Н .
На воде с перекосом вектора силы тяги в 5 град ракету развернет на 12 град. за 0,84 сек.
После этого ее дополнительно развернет на пневмовыхлопе на 1,5 град за 1,4 сек.
Итого перед выходом в инерциальный полет полный разворот на активном участке составит 13,5 град. за 2,24 сек. Данные силы тяги на пневмовыхлопе взяты из программы Gematogen'а.
Хочу отметить также, что в конце воды (при t=0,72 сек) ЦТ ракеты переходит ЦД и ракета становится аэродинамически устойчивой.
Дальнейшему развороту от перекоса препятствует сила аэродинамического сопротивления. В то время как до этого, эта сила наоборот помогала еще больше разворачивать ракету.
Еще раз отмечу, что данная методика позволяет рассчитывать разворот ракеты в зависимости от перекоса сопла на активном участке и для ракет с любым типом двигателя. Разницы никакой.
Прикреплённые файлы:


Это сообщение редактировалось 03.11.2012 в 19:32
Copyright © Balancer 1997..2024
Создано 24.04.2009
Связь с владельцами и администрацией сайта: anonisimov@gmail.com, rwasp1957@yandex.ru и admin@balancer.ru.
Создано 24.04.2009
Связь с владельцами и администрацией сайта: anonisimov@gmail.com, rwasp1957@yandex.ru и admin@balancer.ru.
 Ckona
Ckona

 инфо
инфо инструменты
инструменты PopovIgor
PopovIgor