Концепция, доктрина и корабельный состав современного ВМФ России

A.I.>>> КВВМКУ - это Калининград или Баку?
Popsicle>> Баку. В Калининграде--КВВМУ. Каспийское было Краснознамённым.
A.I.> кузница кадров!

Ну начиная с морпеха в Сталинграде до Адмирала Жильцова до Саши Турилина. Так и было. Быв. Начальник ВМА Адмирал Сысуев--тоже наш. Почти весь комкорпус МЧ ПВ-БОХР--тоже наш.

Popsicle> Ну начиная с морпеха в Сталинграде до Адмирала Жильцова до Саши Турилина. Так и было. Быв. Начальник ВМА Адмирал Сысуев--тоже наш. Почти весь комкорпус МЧ ПВ-БОХР--тоже наш.

Уррра!!! Правда в Америке и кукушка Попсикл зовется (или считает себя) соловьем и нууу очень нуждается в совершенствовании своих древних знаний о ВМФ России. Кукуйте дальше, я вам не помощник.

Popsicle> Ну вообщем-то как и ожидалось. Ответ ни о чём.
Ну если вы хотите конкретики то вот: вы болтун и фанфарон.

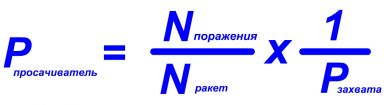
Popsicle> Меня не интересуют обложки книжек--меня интересует можете ли вы посчитать Поисковую Производительность, и знаете ли вы что такое FER. Сможете ли вы рассказать что это такое (см. ниже). Я могу. Точнее я вообще на этом свои заключения строил и строю с момента выпуска. Для примера, формула формула вероятности просачивателя.


Уже то, что вы приводите не отечественную терминологию говорит о том, что вы слабо знакомы даже с элементарным матаппаратом. Соответственно вы не знакомы и с более сложным матаппаратом, используемом в более сложных системах и при детальном моделировании.

В отечественно военно-морской науке, полная вероятность поражения цели при независимых выстрелах и разной вероятности попадания записывается так:


Кстати, данная формула, правда при небольшой корректировке, использовалась при расчетах по обоснованию объема НКЗ сабжа. Догадаетесь, какой именно корректировке она подверглась?
Для человека, по настоящему знакомого с исследованием операций это не должно составить проблемы.
Да, еще одно, напомните всем, что еще я пропустил в описании формулы полной вероятности, при каком предположении она выведена?

PS. Раз уж вы уже так себя расхваливаете, может и мне стоит сказать, что я не только отучился в ВМА (о чем можно было бы догадаться по обложке книги), но и имею кандидатскую степень по соответствующей специальности непосредственно касающейся данных вопросов. Так, что давайте, когда захотите меня еще спросить, готовьте плату за консультацию.

Ну вы ещё подеритесь горячие финские парни.

LtRum> PS. Раз уж вы уже так себя расхваливаете, может и мне стоит сказать, что я не только отучился в ВМА (о чем можно было бы догадаться по обложке книги)
Книга издана в 1969г. И к этому времени её писатель должен как минимум лет 20 корпеть в науке. Ясен пень что не сразу после школьной парты.
Сколько же вам лет? По моим подсчётам - 100, или... 110.
Надо же. Долгих вам лет и крепкой памяти.

P.S. А на каком корабле встретили День Победы?

LtRum> Ну если вы хотите конкретики то вот: вы болтун и фанфарон.

От вас я ничего не хочу, но коли вопросы поставлены то позвольте ответить и более не беспокоить вас. Да и отвечаю я по сути не вам а тем, кто это читает. По пунктам:

LtRum>
LtRum> Уже то, что вы приводите не отечественную терминологию говорит о том, что вы слабо знакомы даже с элементарным матаппаратом. Соответственно вы не знакомы и с более сложным матаппаратом, используемом в более сложных системах и при детальном моделировании.
LtRum> В отечественно военно-морской науке, полная вероятность поражения цели при независимых выстрелах и разной вероятности попадания записывается так:
LtRum>

Это тоже самое, что я вывесил вам, только с показом произведения, вы же--с использованием Пи заглавного как произведения, то же самое как использование Сигмы заглавной как суммы, вместо того, чтобы расписывать всю сумму до n-ного слагаемого. Если вас очковтирательство устраивает--на здоровье. Да только видимо пословица "те же яйца, только вид сбоку" вам не знакома.


LtRum> Кстати, данная формула, правда при небольшой корректировке, использовалась при расчетах по обоснованию объема НКЗ сабжа. Догадаетесь, какой именно корректировке она подверглась?

Нет, не догадаюсь поскольку не знаю что такое НКЗ и сабж, я не шучу. Вы абсолютно верно отметили, что по сути я представил формулу вероятности поражения для ЗАЛПА. Вероятность же просачивателя выводится по формуле (вы увидите её в конце). Суть всех этих формул в Омеге, коя является эмпирической пременной и есть результат как испытаний так и боевого применения оружия, а проще говоря--опыта. Критерий эффективности как правило--вероятность поражения. Омеги могут меняться. Также как меняются и коэффициэнты в Залповой Модели.

LtRum> Для человека, по настоящему знакомого с исследованием операций это не должно составить проблемы.
LtRum> Да, еще одно, напомните всем, что еще я пропустил в описании формулы полной вероятности, при каком предположении она выведена?

Не знаю, что вы имеете ввиду.

LtRum> PS. Раз уж вы уже так себя расхваливаете, может и мне стоит сказать, что я не только отучился в ВМА (о чем можно было бы догадаться по обложке книги), но и имею кандидатскую степень по соответствующей специальности непосредственно касающейся данных вопросов. Так, что давайте, когда захотите меня еще спросить, готовьте плату за консультацию.

Ни вы, ни ваши консультации мне абсолютно не интересны. Если же вы считаете что частные производные или дифференциальные уравнения (не говоря уже о линейном программировании)--это какой-то особенный матаппарат, я вам позволю напомнить, что в тех же Советских ВВМУЗ высшая математика читалась вплоть до Дифференциальных Уравнений (и я не имею ввиду с разделяемыми переменными--это уровень 11 класса любой нормальной школы) а Теория Вероятности преподавалась, если мне склероз не изменяет на втором курсе. Включая все прелести дискретных случайных переменных. Математические же ожидания (вас Сигма запись МО через xp(x), где x:p(x)>0 устроит?) рассчитывались в ряде предметов, включая МОАНИ и ТИО. Если же вы кандидат наук из поколения Пепси я ничему не удивлюсь, и похоже таковым вы и являетесь. Зосим, позвольте моему фанфаронству и болтунству откланяться, потому как чтение тезисов тех же постградов из того же Ньюпорта (как раз по Залповым Моделям и ТИО) и общение с менее аггрессивными товарищами, некоторые даже доктора наук, мне представляются намного более содержательным и обогощающим нежели пикироваться с вами. Приятно оставаться.

ЗЫ. По поводу "детального моделирования", если есть желание--ознакомьтесь как раз с тезисами Naval post-Graduate School или даже Австралийцами с Сингапуриянами.

Lot-2> Сколько же вам лет? По моим подсчётам - 100, или... 110.
А вам? 10 или 12?
Я не автор сей книги.

Lot-2> Надо же. Долгих вам лет и крепкой памяти.
А вам учится, учится и еще раз учится.

[size=100]Popsicle> ...(и я не имею ввиду с разделяемыми переменными--это уровень 11 класса любой нормальной школы) а Теория Вероятности...

Теория вероятностей Пока бесплатная консультация

Popsicle> Нет, не догадаюсь поскольку не знаю что такое НКЗ и сабж, я не шучу.
Сабж=пр.1144, НКЗ = надводная конструктивная защита.

Popsicle> Вы абсолютно верно отметили, что по сути я представил формулу вероятности поражения для ЗАЛПА.
Формула выведена из предположения, что вероятности попадания независимы, поэтому применение данной формулы для залпа ПКР не всегда верно. Надеюсь вы знаете, что такое независимые события?
В вероятность попадания входит и вероятность преодоления противодействия (ЗОС, РЭВ), которое может зависить друг от друга при залповой стрельбе ПКР.

Popsicle> Суть всех этих формул в Омеге, коя является эмпирической пременной
это матожидание числа попаданий, необходимого для поражения цели, поэтому она может определятся и расчетными методами.
Говорить, что в ней суть - ну это как-то по детски, что ли.

LtRum>> Да, еще одно, напомните всем, что еще я пропустил в описании формулы полной вероятности, при каком предположении она выведена?
Popsicle> Не знаю, что вы имеете ввиду.
Любая матмодель составляется при определенных допущениях и предположениях.
В данном случае допущение - независимось , а также - показательный закон поражения цели. Несоблюдение данных условий делает применение данной формулы неверным.

LtRum> А вам? 10 или 12?
Пришёл, увидел и рискнул обидеть. Напрасно, очень напрасно.
Смешаю, сами понимаете с чем.

LtRum> Я не автор сей книги.
Не автор, не учился в ВМА, а тогда к чему этот пассаж -
"Раз уж вы уже так себя расхваливаете, может и мне стоит сказать, что я не только отучился в ВМА (о чем можно было бы догадаться по обложке книги)"

LtRum> А вам учится, учится и еще раз учится.
Спасибо за добрый совет, форева.

pytnic>> Наши пытались "Гюрзу" по фото и схемкам сделать - ну не идёт в радийку 600! на поворотах валит.
pytnic>> Может, эта версия будет более ходовой?
I.M.> Ну это "болезнь" моделей речных кораблей, с низкой осадкой и развитой надстройкой.

Знаю..
Для прямоходов EK 600 еще годятся, а на радийку...
Я с этим еще мальчишкой столкнулся, когда попытался на проект 1125 Радио поставить. Как сейчас помню - РУМ 2 называлось(((
УТОПИЛ...

Прошу прощения, а какое отношение наша беседа о мореходности "Гюрзы" и её предшественников имеет к "АРК?

Lot-2> Пришёл, увидел и рискнул обидеть. Напрасно, очень напрасно.
Это вы такой смелый?

Lot-2> Смешаю, сами понимаете с чем.
Вы? Смешно.

LtRum>> Я не автор сей книги.
Lot-2> Не автор, не учился в ВМА, а тогда к чему этот пассаж -
Вы может и не учились, не в курсе.

Lot-2> "Раз уж вы уже так себя расхваливаете, может и мне стоит сказать, что я не только отучился в ВМА (о чем можно было бы догадаться по обложке книги)"
Ну наверное потому, чтобы намекнуть, о месте учебы, нет?

LtRum>> А вам учится, учится и еще раз учится.
Lot-2> Спасибо за добрый совет, форева.
Идите, не подаю.

LtRum> Любая матмодель составляется при определенных допущениях и предположениях.
LtRum> В данном случае допущение - независимось , а также - показательный закон поражения цели. Несоблюдение данных условий делает применение данной формулы неверным.

Всегда интересно смотреть , как применяется математический аппарат в прикладных задачах.

1)Посмотрел сингапурцев-австралийцев (включая референс-лист)по ссылке участника форума Popsicle. Неприятно удивился, не увидев первоисточник "просачиваний" - "Percolation Theory for Mathematics " H.Kesten, 1982. Может быть потому, что принятый термин percolation австралосингапурцы заменили на leakage ))) Статья, конечно , совсем незатейливая. Но ,наверное, имеет право на "жизнь" - поскольку опубликована))

2) Книга Кестена, посвященная изучению свойств модели Изинга - добротная. Но для советской\российской математической школы - не более). Хотя бы потому , что с 1962 года на Мехмате выдающимся нашим математиком Роландом Львовичем Добрушиным с коллегами был создан и очень плодотворно работал семинар по статистической физике, в том числе в области изучения распределения Гиббса на решётках , а оценки критических чисел в модели Изинга - в данной проблематике всего лишь частная задача) . Для интересующихся - в 2013 году в ИППИ (Институт Проблем передачи информации) РАН был опубликован обстоятельный отчёт (с основными результатами)о работе мехматовского семинара. Авторы - ведущие участники семинара (Минлос, Пирогов, Печерский)

3) Из комментария участника LtRum о требовании "независимости событий" можно предположить , что для обсуждаемых в форуме оценках вероятности поражения\проникновения возможно использование более сложной модели, чем модель независимых испытаний (переход от модели , не имеющей "памяти" (схема независимых испытаний), к модели с " небольшой конечной памятью" ( марковский процесс)). Да , "марковская модель" хорошо описывает большой класс таких случайных систем . И что не менее важно , допускает численное моделирование. Конечно , по сравнению с моделью независимых испытаний вычислительные сложности существенно возрастут , но реально разрешимы. Проверено).

4) Если уважаемый LtRum сочтёт возможным дать ссылки на работы, использующие такую модель в обсуждаемых приложениях - мне было бы интересно посмотреть .

Mikey> 2) ... Для интересующихся - в 2013 году в ИППИ (Институт Проблем передачи информации) РАН был опубликован обстоятельный отчёт (с основными результатами)о работе мехматовского семинара. Авторы - ведущие участники семинара (Минлос, Пирогов, Печерский)
Спасибо.

Mikey> 3) ...возможно использование более сложной модели, чем модель независимых испытаний (переход от модели , не имеющей "памяти" (схема независимых испытаний), к модели с " небольшой конечной памятью" ( марковский процесс)).
Да такие модели используются, но уравнения на базе ур-я Колмогорова используются тоже.

Mikey> Да , "марковская модель" хорошо описывает большой класс таких случайных систем . И что не менее важно , допускает численное моделирование. Конечно , по сравнению с моделью независимых испытаний вычислительные сложности существенно возрастут , но реально разрешимы. Проверено).
Полностью согласен.

Mikey> 4) Если уважаемый LtRum сочтёт возможным дать ссылки на работы, использующие такую модель в обсуждаемых приложениях - мне было бы интересно посмотреть .
Да вот не могу, и не потому, что не знаю.
Из открытого можно порекомендовать
Худяков Л.Ю. Исследовательское проектирование кораблей.

LtRum> Это вы такой смелый?
LtRum> Вы? Смешно.
LtRum> Идите, не подаю.
Оказалось, что вы не уважаемый пенсионер, а юный "пионер".
К тому же борзой как петушок. Прокукарекал, интернет стерпит и ответку держать не придётся. Назначать вам встречу - не придёте, проверено.
Значит - ПНХ.

LtRum> Ну наверное потому, чтобы намекнуть, о месте учебы, нет?
Понимаете, читая вашу писанину в этой и других ветках, у меня сложилось стойкое убеждение о том, что ваше образование далеко не морское и даже не военное.

Lot-2> Понимаете, читая вашу писанину в этой и других ветках, у меня сложилось стойкое убеждение о том, что ваше образование далеко не морское и даже не военное.
Вам просто не хватает кругозора.

LtRum>> Любая матмодель составляется при определенных допущениях и предположениях.
LtRum>> В данном случае допущение - независимось , а также - показательный закон поражения цели. Несоблюдение данных условий делает применение данной формулы неверным.
Mikey> Всегда интересно смотреть , как применяется математический аппарат в прикладных задачах.
Mikey> 1)Посмотрел сингапурцев-австралийцев (включая референс-лист)по ссылке участника форума Popsicle. Неприятно удивился, не увидев первоисточник "просачиваний" - "Percolation Theory for Mathematics " H.Kesten, 1982. Может быть потому, что принятый термин percolation австралосингапурцы заменили на leakage ))) Статья, конечно , совсем незатейливая. Но ,наверное, имеет право на "жизнь" - поскольку опубликована))


Мне кажется, причём ничего личного, что вы немного расплодили сущностей. НЕ имеет значения КТО впервые ввёл термин Leaker (просачиватель) так же как и его производные, но на данный момент та же военно-морская (и не только) англосфера использует его очень широко. Это уже давно стандартный термин в ТИО и является, объективно, основной задачей флотов то ли по обеспечению вот этих самых просачивателей, то ли защиты от них. То, что вы прочитали (???) никакая не статья--это часть тезиса Капитана ВС Сингапура Кита Хо на получение звания Магистра (Интегрирование Систем). Написано это под руководством возможно самого блестящего современного оперативного ума в ВМС США, Капитана Уэйна Хъюза--Начальникак Кафедры Теории Исследования Операций в Naval Post-Graduate School в Монтеррее. То что Хо пишет в своём тезисе имеет огромное значение для тех, кто изучает Сетецентрику и проблемы Распределённой Летальности, которые на сегодня определяют ход дискуссии не только в ВМС США но и глобально. Кто такой Хъюз и каков его статус в ВМС США--если заинтересует, свистните, будет отдельное время расскажу поподробнее. Вопрос Залповых (включая Расширенные) Уравнений в современной ракетной парадигме--да ни один серьёзный командир оперативного уровня без них не рассматривает войну на море да и не только на море.

Runoske> Это точно, впаривают государству корабли по инерции, без умысла. Вроде сто раз уже намекали про бесперспективность МРК и МПК, ан нет
Runoske> У вас ссылки на pdf нет ? Разберём на форуме Я даже готов перевести самые противоречивые части, чтобы нашего истинного патриота тоже включить в обсуждение

Разбирай.

Вроде сто раз уже намекали про бесперспективность МРК и МПК, ан нет


Для "специалистов", ссылка.

Каспийская флотилия начала наносить удары по ИГИЛ в Сирии

Spinch> не пора ли вынести парадигмеров из темы про крейсера 1144?

Давно пора...Когда маловато мозгов,подключают угрозы...Знакомо...

Popsicle> Разбирай.

запилил сюда

LtRum> Проецирование собственного поведения на других. 
LtRum> И да, отдельно, за трусость.

"Хоботов! Это мелко!"
Я отписал вам в ЛС.

Lot-2> Я отписал вам в ЛС.
"Вспылил, был неправ."©
Приношу свои извинения.