-
![[image]](https://www.balancer.ru/cache/sites/w/w/www.afterwork.com.ua/wp-content/uploads/2011/03/128x128-crop/launcher_a2.jpg)
Обыкновенные водяные ракеты из пластиковых бутылок
Теги:
SashaPro> Смотри, я уже прикинул.
Отличная иллюстрация того, что точный расчет требует точного описания конструктива ракеты и изучения соответствующего софта.
Насчет тени - за первой ступенью создается разрежение (суть - аэродинамическое сопротивление), которое уменьшается при торчащей центральной части. Вот только учесть "на пальцах" это сложновато.
Отличная иллюстрация того, что точный расчет требует точного описания конструктива ракеты и изучения соответствующего софта.
Насчет тени - за первой ступенью создается разрежение (суть - аэродинамическое сопротивление), которое уменьшается при торчащей центральной части. Вот только учесть "на пальцах" это сложновато.


RocKI> С некоторыми оговорками, достаточно пересчитать эту площадь на обычные стабилизаторы типа крыло и прикинуть в проге.
Я именно об этом - требуются отдельные расчеты. По трудоемкости сравнимые с расчетом собственно положения ЦД.
RocKI> Со сложными формами конечно не все так очевидно, однако...
RocKI> Для моделирования этого процесса, вполне можно заменить бустер цилиндрическим телом, имеющим конический переход на вторую ступень. Площадь конического перехода должна соответствовать суммарной площади обтекателей бустера.
И применить к бустеру иной коэффициент аэродинамического сопротивления. Какой?
Я именно об этом - требуются отдельные расчеты. По трудоемкости сравнимые с расчетом собственно положения ЦД.
RocKI> Со сложными формами конечно не все так очевидно, однако...
RocKI> Для моделирования этого процесса, вполне можно заменить бустер цилиндрическим телом, имеющим конический переход на вторую ступень. Площадь конического перехода должна соответствовать суммарной площади обтекателей бустера.
И применить к бустеру иной коэффициент аэродинамического сопротивления. Какой?


SashaPro> глазок у меня, как у художника-инженера, точный. Диаметры бутылок соответствуют,
Приветствую тебя, Точный Глаз !
В ближайшее время повторю эскиз с указанием диаметров бутылок и линейных размеров.
В целом - очень интересно.
Конечно, есть несоответствия (бутылки первой ступени имеют диаметр 110 мм, а не 78 мм, как у второй, стартовая масса ракеты не 28 кГ (а чего... сделаем !), а 7,4 кГ),
но это мелочи и быстро исправляется.
Распределение масс другое, вернусь с работы - уточню (в виде набора цилиндров).
Нечто похожее считает мой старенький AutoCad, но конечно, без аэродинамики.
Приветствую тебя, Точный Глаз !
В ближайшее время повторю эскиз с указанием диаметров бутылок и линейных размеров.
В целом - очень интересно.
Конечно, есть несоответствия (бутылки первой ступени имеют диаметр 110 мм, а не 78 мм, как у второй, стартовая масса ракеты не 28 кГ (а чего... сделаем !), а 7,4 кГ),
но это мелочи и быстро исправляется.
Распределение масс другое, вернусь с работы - уточню (в виде набора цилиндров).
Нечто похожее считает мой старенький AutoCad, но конечно, без аэродинамики.


RocKI> Речь шла о положении ЦД. Сопротивление там не при чем.
На самом деле - очень даже причем, особенно при малых углах отклонения.
Просто мы считаем в допущении, что Сх одинаков для всех частей ракеты.
Сх конуса и группы конусов существенно отличается, так как внутренняя часть группы конусов не имеет во внутренней части выхода (достаточно свободного) для воздуха обтекающего конус.
Мы все здесь конечно "знатные аэродинамики", но все-же...
Корпус обычной бутылки - это конус сопряженный с длинным цилиндром.
Аэродинамическое сопротивление конуса - 0,5 при угле вершины 60 градусов.
Сх длинного цилиндра 0.82, Сх короткого цилиндра 1,15, Сх плоской тарелки 1,17.
Очевидно, что длинный цилиндр улучшает условия обтекания в задней части объекта снижая тем самым Сх. Поэтому если за конусом поставить цилиндр, то Сх снизится.
В случае, если конус заменен полусферой или другим телом вращения с выпуклыми образующими, Сх также снижается. Еще он зависит от степени конусности.
Я в своих расчетах принял Сх=0,4. Игорь принимает Сх=0,3.
Могу предположить, что сопротивление обратного конуса с длинным цилиндром не меньше Сх длинного цилиндра. А сама первая ступень Алексея - скорее короткий цилиндр, чем длинный. Я думаю, что Сх перой ступени находится между Сх конуса с длинным цилиндром и Сх обратного конуса с коротким цилиндром. Причем ближе к последнему. Т.е. порядка 0,8 - 1,1. А это (учитывая площади сечений) непосредственно влияет на положение ЦД.
Получается, что для корректного расчета при малых углах отклонения (до 10 градусов) необходимо брать вертикальную проекцию ракеты и применять коэффициенты для площадей с существенно отличным Сх. В том числе для заднего среза, если он не конический.
На самом деле - очень даже причем, особенно при малых углах отклонения.
Просто мы считаем в допущении, что Сх одинаков для всех частей ракеты.
Сх конуса и группы конусов существенно отличается, так как внутренняя часть группы конусов не имеет во внутренней части выхода (достаточно свободного) для воздуха обтекающего конус.
Мы все здесь конечно "знатные аэродинамики", но все-же...
Корпус обычной бутылки - это конус сопряженный с длинным цилиндром.
Аэродинамическое сопротивление конуса - 0,5 при угле вершины 60 градусов.
Сх длинного цилиндра 0.82, Сх короткого цилиндра 1,15, Сх плоской тарелки 1,17.
Очевидно, что длинный цилиндр улучшает условия обтекания в задней части объекта снижая тем самым Сх. Поэтому если за конусом поставить цилиндр, то Сх снизится.
В случае, если конус заменен полусферой или другим телом вращения с выпуклыми образующими, Сх также снижается. Еще он зависит от степени конусности.
Я в своих расчетах принял Сх=0,4. Игорь принимает Сх=0,3.
Могу предположить, что сопротивление обратного конуса с длинным цилиндром не меньше Сх длинного цилиндра. А сама первая ступень Алексея - скорее короткий цилиндр, чем длинный. Я думаю, что Сх перой ступени находится между Сх конуса с длинным цилиндром и Сх обратного конуса с коротким цилиндром. Причем ближе к последнему. Т.е. порядка 0,8 - 1,1. А это (учитывая площади сечений) непосредственно влияет на положение ЦД.
Получается, что для корректного расчета при малых углах отклонения (до 10 градусов) необходимо брать вертикальную проекцию ракеты и применять коэффициенты для площадей с существенно отличным Сх. В том числе для заднего среза, если он не конический.


RocKI> Устойчивость определяет Су.
А что это такое?
Просто намек на смену осей координат?
Или действительно что-то серьезное?
На самом деле - не знаю! Соответственно нахожусь в неопределенности - расстраиваться или нет.
А что это такое?
Просто намек на смену осей координат?

Или действительно что-то серьезное?
На самом деле - не знаю! Соответственно нахожусь в неопределенности - расстраиваться или нет.



RocKI>> Устойчивость определяет Су.
Gematogen> А что это такое?
Если ракета летит со строго нулевым углом атаки, точка приложения аэродинмического сопротивления находится на верхушке обтекателя, и эту верхушку обтекателя запросто можно считать центром давления.
При отклонении на очень малый угол центр давления смещается вниз и по мере роста угла достаточно быстро смещается в точку ЦБС. Поэтому в простейших оценках устойчивости используют ЦБС и ЦМ (центр масс).
В действительности все ракеты летают с вилянием. Но при достаточном запасе устойчивости на малых углах атаки - виляние в пределах менее 0,1 градуса.
Сх - коэффициент в аэродинамич.формуле силы сопротивления в направлении движения ракеты (крыла).
Су - коэффициент той же формулы в направлении перпендикулярно движению ракеты (крыла).
Gematogen> А что это такое?
Если ракета летит со строго нулевым углом атаки, точка приложения аэродинмического сопротивления находится на верхушке обтекателя, и эту верхушку обтекателя запросто можно считать центром давления.
При отклонении на очень малый угол центр давления смещается вниз и по мере роста угла достаточно быстро смещается в точку ЦБС. Поэтому в простейших оценках устойчивости используют ЦБС и ЦМ (центр масс).
В действительности все ракеты летают с вилянием. Но при достаточном запасе устойчивости на малых углах атаки - виляние в пределах менее 0,1 градуса.
Сх - коэффициент в аэродинамич.формуле силы сопротивления в направлении движения ракеты (крыла).
Су - коэффициент той же формулы в направлении перпендикулярно движению ракеты (крыла).


RocKI> Коэффициент подъемной силы...
Я считал, что подъемная сила возникает при обтекании несимметричного профиля в силу разницы давлений. И в нашем примере я ее не усматриваю. Хотя я могу и ошибаться.
Тем не менее, пока я не вижу - как это замечание влияет на суть сказанного. Что-то изменилось?
Я считал, что подъемная сила возникает при обтекании несимметричного профиля в силу разницы давлений. И в нашем примере я ее не усматриваю. Хотя я могу и ошибаться.
Тем не менее, пока я не вижу - как это замечание влияет на суть сказанного. Что-то изменилось?


Ckona> Если ракета летит со строго нулевым углом атаки, точка приложения аэродинмического сопротивления находится на верхушке обтекателя, и эту верхушку обтекателя запросто можно считать центром давления.
Ckona> При отклонении на очень малый угол центр давления смещается вниз и по мере роста угла достаточно быстро смещается в точку ЦБС. Поэтому в простейших оценках устойчивости используют ЦБС и ЦМ (центр масс).
На малый угол - это сколько? ЦД на носу ракеты - это вроде от Бароумана пришло? А доказательства этого есть? Я пока запроста так считать не могу, вот пример на твоей же ракете. Изменил угол атаки с 10гр. до 0,1гр. ЦД уполз не вверх, а вниз и его координата уменьшилась до 761мм с 913мм.
Ckona> При отклонении на очень малый угол центр давления смещается вниз и по мере роста угла достаточно быстро смещается в точку ЦБС. Поэтому в простейших оценках устойчивости используют ЦБС и ЦМ (центр масс).
На малый угол - это сколько? ЦД на носу ракеты - это вроде от Бароумана пришло? А доказательства этого есть? Я пока запроста так считать не могу, вот пример на твоей же ракете. Изменил угол атаки с 10гр. до 0,1гр. ЦД уполз не вверх, а вниз и его координата уменьшилась до 761мм с 913мм.
Прикреплённые файлы:


SashaPro> На малый угол - это сколько? ... ЦД уполз не вверх, а вниз и его координата уменьшилась до 761мм с 913мм.
Тут приходится увиливать от прямого ответа, потому как теорию Барроумана (я нечто похожее и в наших публикациях встречал, кажись, в книжке Эпштейна?) напамять не запомнил. Метод освоил RocKi - и реализовал в расчетной программе.
Рассуждая без аргументов: если угол атаки нулевой, то нет силы, восстанавливающей возмущения. Чтобы такая сила появилась, нужен хоть какой-то угол атаки. Наибольшего значения восстанавливающий момент достигает при движении ракеты с большими углами атаки. Скорее всего, если это "умозрение" разложить по физическим формулам, получим смещение центра давления на малых углах атаки.
В твоем расчете ЦД уполз вниз - причин может быть две. Либо "бутылколет" сложной формы и его обтекание - совсем не "по Барроуману" (он анализировал "классику"). Либо выбранное тобой/твоей программой определение координаты ЦД не совпадает с ... - тоже вполне может быть, легко проверяется расчетом "классики" и сравнением.
Кстати, мне очень интересно - чем отличаются три типа момента инерции, выводимые твоей программой.
Тут приходится увиливать от прямого ответа, потому как теорию Барроумана (я нечто похожее и в наших публикациях встречал, кажись, в книжке Эпштейна?) напамять не запомнил. Метод освоил RocKi - и реализовал в расчетной программе.
Рассуждая без аргументов: если угол атаки нулевой, то нет силы, восстанавливающей возмущения. Чтобы такая сила появилась, нужен хоть какой-то угол атаки. Наибольшего значения восстанавливающий момент достигает при движении ракеты с большими углами атаки. Скорее всего, если это "умозрение" разложить по физическим формулам, получим смещение центра давления на малых углах атаки.
В твоем расчете ЦД уполз вниз - причин может быть две. Либо "бутылколет" сложной формы и его обтекание - совсем не "по Барроуману" (он анализировал "классику"). Либо выбранное тобой/твоей программой определение координаты ЦД не совпадает с ... - тоже вполне может быть, легко проверяется расчетом "классики" и сравнением.
Кстати, мне очень интересно - чем отличаются три типа момента инерции, выводимые твоей программой.


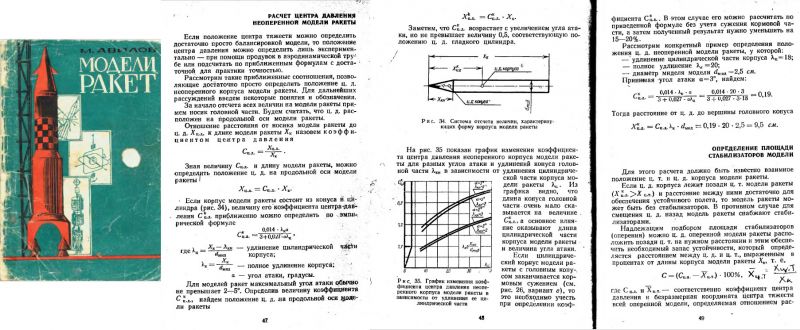
Ckona> я нечто похожее и в наших публикациях встречал
СашаПро ! Специально для тебя порылся и нашел !
Книжка Авилова.
По приведенным формулам при нулевом угле атаки центр давления находится на верхушке ракеты.
Но !
Четкого определения ЦД нет. Я его понимаю как точка приложения аэродинамических сил.
... и тут я все понял. Первая ступень - аэродинамический тормоз, "бутылкопарашют". Все парашютисты летают парашютом "назад".
СашаПро ! Специально для тебя порылся и нашел !
Книжка Авилова.
По приведенным формулам при нулевом угле атаки центр давления находится на верхушке ракеты.
Но !
Четкого определения ЦД нет. Я его понимаю как точка приложения аэродинамических сил.
... и тут я все понял. Первая ступень - аэродинамический тормоз, "бутылкопарашют". Все парашютисты летают парашютом "назад".
Прикреплённые файлы:


Ckona> Рассуждая без аргументов: если угол атаки нулевой, то нет силы, восстанавливающей возмущения.
Именно поэтому нам все-равно, где находится ЦД. Главное - чтобы вектор сопротивления среды проходил через ЦМ. Вопрос ПМСМ относится к чисто философским и не имеет практического значения для расчета устойчивости. При минимальных отклонениях ЦД скачкообразно смещается.
Ckona> ... и тут я все понял. Первая ступень - аэродинамический тормоз, "бутылкопарашют".
Именно.
Именно поэтому нам все-равно, где находится ЦД. Главное - чтобы вектор сопротивления среды проходил через ЦМ. Вопрос ПМСМ относится к чисто философским и не имеет практического значения для расчета устойчивости. При минимальных отклонениях ЦД скачкообразно смещается.
Ckona> ... и тут я все понял. Первая ступень - аэродинамический тормоз, "бутылкопарашют".
Именно.


SashaPro> ...вот пример на твоей же ракете. Изменил угол атаки с 10гр. до 0,1гр.
Мне кажется, что при некруглой форме первой ступени должна наблюдаться анизотропия свойств.
Можно ли рассчитать положение ЦД при малом угле наклона в сторону одного из баллонов первой ступени и между баллонами? (Поворот ракеты вокруг продольной оси на 30 градусов)
Мне кажется, что при некруглой форме первой ступени должна наблюдаться анизотропия свойств.
Можно ли рассчитать положение ЦД при малом угле наклона в сторону одного из баллонов первой ступени и между баллонами? (Поворот ракеты вокруг продольной оси на 30 градусов)


Ckona> По приведенным формулам при нулевом угле атаки центр давления находится на верхушке ракеты.
Там формулы приведены в примере только для ондого случая угла атаки в 3гр. Какие эти формулы будут для 0гр. не известно. Линии на графике коэффициента центра давления есть эти самые формулы. Для каждой линии своя формула.
Ckona> Но !
Ckona> Четкого определения ЦД нет. Я его понимаю как точка приложения аэродинамических сил.
А я его понимаю, как фокус аэродинамических сил, где все их моменты равны нулю.
Ckona> ... и тут я все понял. Первая ступень - аэродинамический тормоз, "бутылкопарашют". Все парашютисты летают парашютом "назад".
Ну и как тут ЦД может быть в носу? Или на пятках парашютиста?
Там формулы приведены в примере только для ондого случая угла атаки в 3гр. Какие эти формулы будут для 0гр. не известно. Линии на графике коэффициента центра давления есть эти самые формулы. Для каждой линии своя формула.
Ckona> Но !
Ckona> Четкого определения ЦД нет. Я его понимаю как точка приложения аэродинамических сил.
А я его понимаю, как фокус аэродинамических сил, где все их моменты равны нулю.
Ckona> ... и тут я все понял. Первая ступень - аэродинамический тормоз, "бутылкопарашют". Все парашютисты летают парашютом "назад".
Ну и как тут ЦД может быть в носу? Или на пятках парашютиста?


Gematogen> Можно ли рассчитать положение ЦД при малом угле наклона в сторону одного из баллонов первой ступени и между баллонами? (Поворот ракеты вокруг продольной оси на 30 градусов)
Можно. Координата ЦД ещё ниже 739мм.
Можно. Координата ЦД ещё ниже 739мм.
Прикреплённые файлы:


Из всей ситуации можно сделать вывод, что на момент инерции в качестве стабилизирующего фактора можно полагаться лишь в течение короткого времени, то есть 0,5-0,7сек. после старта. Далее необходимо подключать аэродинамическую стабилизацию. У Алексея более длинная фаза работы 1-й ступени, вот в конце и начало крутить. Собственно Алексей уже сделал вывод, что необходимы стабилизаторы.
Я провел пробный 3-х ступенчатый старт, у 2-й ступени, как и у 1-й, нет стабилизаторов, результат в соответствие со сделанными выводами. При накачке ракеты воздухом ее заметно искривило, но это не стало фатальным аргументом для дальнейшего развития ситуации, что видно, если смотреть видео по кадрам. Ранее я проводил 3-х ступенчатый старт, но у 2-й были стабилизаторы, старт был с издержками, но значительно лучше.
Ранее и я, и Алексей придерживались мнения, что на 1-й ступени стабилизатор не нужен, как оказалось подобная точка зрения ошибочная.
http://hddfiles.ru/download/20910/
Я провел пробный 3-х ступенчатый старт, у 2-й ступени, как и у 1-й, нет стабилизаторов, результат в соответствие со сделанными выводами. При накачке ракеты воздухом ее заметно искривило, но это не стало фатальным аргументом для дальнейшего развития ситуации, что видно, если смотреть видео по кадрам. Ранее я проводил 3-х ступенчатый старт, но у 2-й были стабилизаторы, старт был с издержками, но значительно лучше.
Ранее и я, и Алексей придерживались мнения, что на 1-й ступени стабилизатор не нужен, как оказалось подобная точка зрения ошибочная.
http://hddfiles.ru/download/20910/
Прикреплённые файлы:


Это сообщение редактировалось 28.10.2012 в 22:00
Брат-2> Я провел пробный 3-х ступенчатый старт
Брат-2 ! Это ФАНТАСТИКА !!!
Твои разделители ступеней на воздушных шариках работают как часы.
Представляю, сколько усердия ты тратишь на исполнение...
Наколько я понимаю, ты хочешь сказать, что в первом запуске со стабилизатором на второй ступени полет получился гораздо стабильнее ?
А к какому запуску относится график высотомера, ко второму ?
Брат-2 ! Это ФАНТАСТИКА !!!
Твои разделители ступеней на воздушных шариках работают как часы.
Представляю, сколько усердия ты тратишь на исполнение...
Наколько я понимаю, ты хочешь сказать, что в первом запуске со стабилизатором на второй ступени полет получился гораздо стабильнее ?
А к какому запуску относится график высотомера, ко второму ?
Прикреплённые файлы:


SashaPro>> 4. Не совпадает с геометрической осью ракеты и координаты ЦУИ (центра угловой инерции), который так же гуляет и меняется по модулям во всех трёх направлениях.
Gematogen> Что такое центр угловой инерции? Я просто не в курсе. Яндекс тоже.
А не вот нашёл, помню же была такая физическая величина: Центр инерции - Физическая энциклопедия
Да, можно было просто написать, ЦИ.
Gematogen> Что такое центр угловой инерции? Я просто не в курсе. Яндекс тоже.
А не вот нашёл, помню же была такая физическая величина: Центр инерции - Физическая энциклопедия
Да, можно было просто написать, ЦИ.


SashaPro> Да, можно было просто написать, ЦИ.
Просто мы его называем центр масс или центр тяжести - поэтому и возникло некоторое недопонимание.
Просто мы его называем центр масс или центр тяжести - поэтому и возникло некоторое недопонимание.


Брат-2> Из всей ситуации можно сделать вывод, что на момент инерции в качестве стабилизирующего фактора можно полагаться лишь в течение короткого времени, то есть 0,5-0,7сек. после старта.
Пока первая ступень - тяжелая.
Брат-2> Ранее и я, и Алексей придерживались мнения, что на 1-й ступени стабилизатор не нужен, как оказалось подобная точка зрения ошибочная.
С точки зрения того, что на первой ступени желательна стабилизация - согласен.
А вот с тем, что стабилизаторы помогут - нет. Они будут находиться слишком близко к ЦМ. Потери на сопротивление при повороте будут слишком велики.
Лучше бороться с причинами отклонения.
Кстати, Алексей именно по этому пути и идет.
А еще я подозреваю, что для эффективного использования многоступенчатой схемы каждая ступень должна быть в разы (4 - 6) тяжелее (мощнее) совокупности последующих ступеней.
Например, если третья ступень литровая, то вторая нужна литров так на пять, а первая - на тридцать. Если соотношение меньше, то результата (высоты) можно добиться на меньшем числе ступеней.
Естественно - если целью является достижение максимальной высоты.
Но я могу и серьезно ошибаться
Пока первая ступень - тяжелая.
Брат-2> Ранее и я, и Алексей придерживались мнения, что на 1-й ступени стабилизатор не нужен, как оказалось подобная точка зрения ошибочная.
С точки зрения того, что на первой ступени желательна стабилизация - согласен.
А вот с тем, что стабилизаторы помогут - нет. Они будут находиться слишком близко к ЦМ. Потери на сопротивление при повороте будут слишком велики.
Лучше бороться с причинами отклонения.
Кстати, Алексей именно по этому пути и идет.
А еще я подозреваю, что для эффективного использования многоступенчатой схемы каждая ступень должна быть в разы (4 - 6) тяжелее (мощнее) совокупности последующих ступеней.
Например, если третья ступень литровая, то вторая нужна литров так на пять, а первая - на тридцать. Если соотношение меньше, то результата (высоты) можно добиться на меньшем числе ступеней.
Естественно - если целью является достижение максимальной высоты.
Но я могу и серьезно ошибаться



Измерил положение ЦМ полностью заправленной ракеты "Пеликан".
Конечно, получается аэродинамическая неустойчивость.
Но повернуть "эту дуру" (а ее и в руках-то тяжело держать, около 8 кГ!) не так-то просто.
По мере расхода топлива первой ступени заметного подъема ЦМ не будет - жидкость "уходит в хвост". Но и момент инерции не сильно будет уменьшаться.
А вот в момент опорожнения будет быстрое изменение координаты ЦМ и момента инерции.
Конечно, получается аэродинамическая неустойчивость.
Но повернуть "эту дуру" (а ее и в руках-то тяжело держать, около 8 кГ!) не так-то просто.
По мере расхода топлива первой ступени заметного подъема ЦМ не будет - жидкость "уходит в хвост". Но и момент инерции не сильно будет уменьшаться.
А вот в момент опорожнения будет быстрое изменение координаты ЦМ и момента инерции.
Прикреплённые файлы:


Ckona> А вот в момент опорожнения будет быстрое изменение координаты ЦМ и момента инерции.
Алексей, ты просто убедился в том, что до момента разделения ракета неустойчива. Ты это и так знал. А что это дало?
Алексей, ты просто убедился в том, что до момента разделения ракета неустойчива. Ты это и так знал. А что это дало?


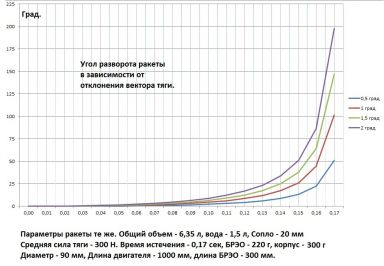
Сделана небольшая программа позволяющая вычислять текущее положение ЦТ, а также с достаточной точностью изменение моментов инерции (по частям и суммарный) относительно изменяющегося положения центра масс, текущие значения углов разворота ракеты в первой стадии работы двигателя (истечение воды).
Дестабилизирующий фактор - угловое отклонение вектора тяги.
Для примера просчитана одноступенчатая ракета с конкретными данными.
На графиках четко прослеживаются основные закономерности.
Данная методика применима и для ракет с ТТРД.
Дестабилизирующий фактор - угловое отклонение вектора тяги.
Для примера просчитана одноступенчатая ракета с конкретными данными.
На графиках четко прослеживаются основные закономерности.
Данная методика применима и для ракет с ТТРД.
Прикреплённые файлы:


Это сообщение редактировалось 29.10.2012 в 18:23
Copyright © Balancer 1997..2024
Создано 24.04.2009
Связь с владельцами и администрацией сайта: anonisimov@gmail.com, rwasp1957@yandex.ru и admin@balancer.ru.
Создано 24.04.2009
Связь с владельцами и администрацией сайта: anonisimov@gmail.com, rwasp1957@yandex.ru и admin@balancer.ru.
 Gematogen
Gematogen

 инфо
инфо инструменты
инструменты Ckona
Ckona