Xan
инфо
инструменты
Massaraksh
Xan
Xan
Реклама Google — средство выживания форумов :)
-
![[image]](https://www.balancer.ru/cache/sites/ru/fa/fastpic/i93/big/2017/0624/25/128x128-crop/7a2e6c7accfee75b5f9ff37387a71d25.jpg)
Вопросы и ответы
(Когда не находишь ответ на форуме, спрашивай!)Теги:
Xan>>>> Справа: реальные струйки из-за поворота в сопле не движутся по прямым, а за счёт инерции немного колеблются относительно прямого пути.
SashaMaks> Этого нет.
Это надо как-то визуализировать только дельту вектора скорости от идеального радиального (из вершины конуса).
ЗЫ
Картинки красивые, такое всегда радует!
SashaMaks> Этого нет.
Это надо как-то визуализировать только дельту вектора скорости от идеального радиального (из вершины конуса).
ЗЫ
Картинки красивые, такое всегда радует!
Вопрос физикам - Xan, Андрей Суворов, Rocki, SashaMax, может кто-то ещё знает.
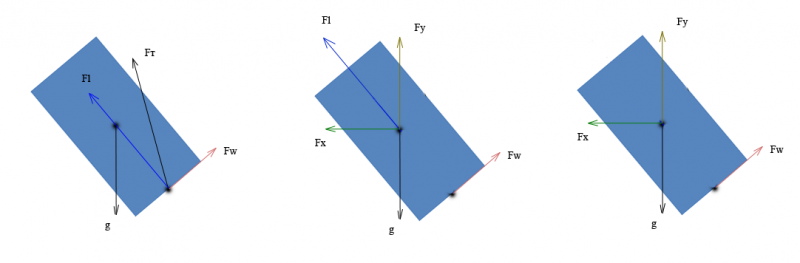
Вопрос по физике, точнее, по динамике (для простоты возьмём двумерный случай):
Хочу смоделировать движение ракеты в упрощённом виде, исходя из двух сил: тяги и силы тяжести. Что мне непонятно - как определяется точка приложения тяги.
Из практики мы знаем, что в данном случае (см. рисунок) ракета полетит вверх и будет поворачиваться влево.
Где правильно?
Если на правом рисунке, то как считается результирующая(ие) сила(ы)?
Если на левом рисунке, то за счет чего ракета будет поворачиваться?
Вопрос по физике, точнее, по динамике (для простоты возьмём двумерный случай):
Хочу смоделировать движение ракеты в упрощённом виде, исходя из двух сил: тяги и силы тяжести. Что мне непонятно - как определяется точка приложения тяги.
Из практики мы знаем, что в данном случае (см. рисунок) ракета полетит вверх и будет поворачиваться влево.
Где правильно?
Если на правом рисунке, то как считается результирующая(ие) сила(ы)?
Если на левом рисунке, то за счет чего ракета будет поворачиваться?
Прикреплённые файлы:
Massaraksh> Где правильно?
Massaraksh> Если на правом рисунке, то как считается результирующая(ие) сила(ы)?
Massaraksh> Если на левом рисунке, то за счет чего ракета будет поворачиваться?
Рисуешь ось сопла.
И на ней, В ЛЮБОЙ УДОБНОЙ ДЛЯ РАСЧЁТОВ ТОЧКЕ, прикладываешь силу тяги.
Правый рисунок (как частный случай) правильный.
Massaraksh> Если на правом рисунке, то как считается результирующая(ие) сила(ы)?
Massaraksh> Если на левом рисунке, то за счет чего ракета будет поворачиваться?
Рисуешь ось сопла.
И на ней, В ЛЮБОЙ УДОБНОЙ ДЛЯ РАСЧЁТОВ ТОЧКЕ, прикладываешь силу тяги.
Правый рисунок (как частный случай) правильный.
Xan> И на ней, В ЛЮБОЙ УДОБНОЙ ДЛЯ РАСЧЁТОВ ТОЧКЕ, прикладываешь силу тяги.
Xan> Правый рисунок (как частный случай) правильный.
Спасибо. Но за счет чего ракета повернется? Если я просто посчитаю результирующую силу, к какой точке я её должен применить?
Xan> Правый рисунок (как частный случай) правильный.
Спасибо. Но за счет чего ракета повернется? Если я просто посчитаю результирующую силу, к какой точке я её должен применить?
Xan>> И на ней, В ЛЮБОЙ УДОБНОЙ ДЛЯ РАСЧЁТОВ ТОЧКЕ, прикладываешь силу тяги.
Xan>> Правый рисунок (как частный случай) правильный.
Massaraksh> Спасибо. Но за счет чего ракета повернется? Если я просто посчитаю результирующую силу, к какой точке я её должен применить?
На экзамене:
-- Что нужно сделать, чтобы забор не повалило ветром?
-- Найти равнодействующую сил давления и в точке её приложения просверлить дырку!
К какой удобно. Точка приложения силы — это математическая абстракция, не более того. Тебя интересует плечо действия силы относительно центра масс, оно-то и разворачивает ракету.
Xan>> Правый рисунок (как частный случай) правильный.
Massaraksh> Спасибо. Но за счет чего ракета повернется? Если я просто посчитаю результирующую силу, к какой точке я её должен применить?
На экзамене:
-- Что нужно сделать, чтобы забор не повалило ветром?
-- Найти равнодействующую сил давления и в точке её приложения просверлить дырку!
К какой удобно. Точка приложения силы — это математическая абстракция, не более того. Тебя интересует плечо действия силы относительно центра масс, оно-то и разворачивает ракету.
Sandro>Тебя интересует плечо действия силы относительно центра масс, оно-то и разворачивает ракету.
Математически это как выражается?
Математически это как выражается?
Sandro>>Тебя интересует плечо действия силы относительно центра масс, оно-то и разворачивает ракету.
Massaraksh> Математически это как выражается?
Massaraksh> Математически это как выражается?
1.1.3. Момент силы относительно точки и оси. Пара силМомент силы относительно центра. Опыт показывает, что эффект дей-ствия силы, приложенной к телу (например, к рычагу, штурвалу) на разных расстояниях от точки закрепления тела, зависит от так называемого м о м е н т а с и л ы относительно точки закрепления.Моментом силы относительно центра О называется произведение модуля силы на кратчайшее расстояние от центра О до линии действия силы. (1.6) где h - кратчайшее расстояние от центра О до линии действия силы Момент силы считается положительным, если сила стремится повернуть тело вокруг центра О против хода часовой стрелки и отрицательным, если по ходу часовой стрелки (рис. 1.24, 1.25). Размерность момента силы Н*м. Рис. 1.24 Рис. 1.25Момент силы не изменяется при переносе точки приложения силы вдоль ее линии действия. Момент силы относительно центра О равен нулю, если сила равна нулю или, если линия действия силы проходит через центр О (плечо рав-но нулю). Графически абсолютная величина момента силы относительно центра О вы-ражается удвоенной площадьюОАВ = 2SОАВМомент силы относительно центра как векторное произведение. Введенного понятия "момент силы относительно центра как алгебраическая ве-личина" оказывается недостаточно в случае сил, произвольно расположенных в пространстве. Плоскости поворота у разных сил будут различными и должны задаваться дополнительно. Удобно ввести понятие "момент силы относительно центра как в е к т о р", модуль которого равен произведению модуля силы на ее плечо, а направление перпендикулярно плоскости, проходящей через линию действия силы и центр момента. Вектор момента силы прикладывают в центре момента и направляют в сторону, откуда сила видна вращающей тело в направлении, противоположном ходу часовой стрелки (рис. 1.26). Соединим центр момента О с точкой приложения силы радиусом-вектором и найдем векторное произведение По определению векторного произведения его модуль||= 2SОАВМодуль вектора момента силы акже равен удвоенной площади ОАВ =Направление векторного произведения также совпадает с направлением вектора момента. Следовательно, вектор-момент силыотносительно центра О можно рассматривать как векторное произведение радиус-векторапроведенного из этой точки в точку приложения силы, на вектор силы Рис. 1.26 Рис. 1.27Момент силы относительно оси. Чтобы охарактеризовать вращательный эффект, создаваемый силой, стремящейся повернуть тело вокруг некоторой оси, вводится понятие "момента силы относительно оси". Рассмотрим твердое тело, которое может вращаться вокруг оси OZ (рис.1.27). Пусть на тело действует сила приложенная в точке А. Проведем через точку А плоскость OXY, перпендикулярную оси OZ, и разложим силу на две составляющие:параллельную оси OZ, и , лежащую в плоскости XY. Составляющая, параллельная оси OZ, крутящего момента не создает, а, следовательно, весь вращательный эффект, создаваемый силой ,будет вызван ее составляющей Моментом силы относительно оси называют момент проекции этой силы на плоскость, перпендикулярную оси, относительно точки пересечения оси с этой плоскостью. Момент силы относительно оси считается положительным, если смотря навстречу оси Z, можно видеть проекцию < стремящейся вращать плоскость XY вокруг оси Z в сторону, противополож-ную вращению часовой стрелки. Момент силы относительно оси равен нулю: 1) если=0, т.е. линия действия силы параллельна оси OZ;2) если h = 0, т.е. линия действия силы пересекает ось OZ.Следовательно, если сила и ось лежат в одной плоскости, то момент силы относительно этой оси равен нулю. Пара сил. Момент пары. Система двух равных по модулю, параллельных и противоположно направленных сил называется п а р о й с и л (рис. 1.28). Пара сил не имеет равнодействующей и силы пары не уравновешиваются. Действие пары на тело характеризуется ее моментом. 1. Вектор-момент перпендикулярен плоскости действия пары. 2. Направлен в ту сторону, чтобы, смотря с его конца, вращение было происходящим против хода часовой стрелки. 3. Величина вектора равна в выбранном масштабе численному значению момента пары.Вектор-момент пары равен векторному произведению радиуса-вектора на ту из сил пары, к началу которой направлен вектор (1.10)или (1.11)по модулю (1.12)Пары сил в пространстве эквивалентны, если их моменты геометрически равны. Геометрическая сумма моментов составляющих пар сил равна моменту эквивалентной им пары т.е. () (1.13)Пары сил, произвольно расположенные в пространстве, взаимно уравно-вешиваются в том случае, если геометрическая сумма их моментов равна нулю. Если пары сил расположены в одной плоскости, то моменты этих пар сил, на-правленные по одной прямой, складываются а л г е б р а и ч е с к и. Момент пары сил, эквивалентный системе пар сил на плоскости, равен алгеб-раической сумме моментов составляющих пар (рис. 1.29). где . Пары сил, расположенные в одной плоскости, взаимно уравновешиваются, если алгебраическая сумма их моментов равна нулю Рис. 1.28 Рис. 1.29Силовое воздействие на самолет часто приводится к паре сил. Например, аэродинамические силы (силы сопротивления воздуха вращению) воздушного винта складываются в пару, называемую аэродинамическим (реактивным) мо-ментом винта Мв (рис. 1.30). Чем большую мощность развивает двигатель, тем больше реактивный момент, вызывающий крен самолета. Этот момент уравно-вешивают некоторым отклонением элеронов; аэродинамические силы и Y составляют пару с моментом, равным значению реактивного момента воздушного винта и обратным его направлению. Рис. 1.30 Рис. 1.31 Рис. 1.32
(1.13) // www.mehanica-kvs.narod.ru
Sandro> К какой удобно. Точка приложения силы — это математическая абстракция, не более того. Тебя интересует плечо действия силы относительно центра масс, оно-то и разворачивает ракету.
Математическая, а точнее обывательская абстракция - это не точка приложения силы, а так называемое всеми вами "ПЛЕЧО" силы, которого нет. Это частный случай упрощения общего векторного уравнения, чтобы не заморачиваться расчётами и как обычно считать прямые углы, что к счастью, хоть это делать большинство ещё со школы умеет.
Вот далее ты ссылаешься на определение момента силы, я же всё-таки сошлюсь на это:
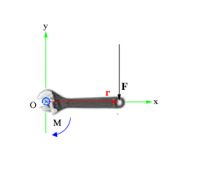
, где момент силы равен векторному произведению радиус-вектора силы на вектор самой силы.
А как же ты будешь без точки приложения искать этот самый радиус-вектор силы???
И не надо сейчас снова всё пытаться сводить к частным случаям плоскости и перпендикулярности, интересует именно произвольное пространственное положение векторов.
Математическая, а точнее обывательская абстракция - это не точка приложения силы, а так называемое всеми вами "ПЛЕЧО" силы, которого нет. Это частный случай упрощения общего векторного уравнения, чтобы не заморачиваться расчётами и как обычно считать прямые углы, что к счастью, хоть это делать большинство ещё со школы умеет.
Вот далее ты ссылаешься на определение момента силы, я же всё-таки сошлюсь на это:
Момент силы — Википедия
L2MT−2 Н·м Дина-сантиметр Псевдовектор Момент силы (синонимы: крутящий момент, вращательный момент, вертящий момент, вращающий момент) — векторная физическая величина, равная векторному произведению радиус-вектора (проведённого от оси вращения к точке приложения силы — по определению) на вектор этой силы. Характеризует вращательное действие силы на твёрдое тело. Понятия «вращающий» и «крутящий» моменты в общем случае не тождественны, так как в технике понятие «вращающий» момент рассматривается как внешнее усилие, прикладываемое к объекту, а «крутящий» — внутреннее усилие, возникающее в объекте под действием приложенных нагрузок (этим понятием оперируют в сопротивлении материалов). // Дальше — ru.wikipedia.org, где момент силы равен векторному произведению радиус-вектора силы на вектор самой силы.
А как же ты будешь без точки приложения искать этот самый радиус-вектор силы???
И не надо сейчас снова всё пытаться сводить к частным случаям плоскости и перпендикулярности, интересует именно произвольное пространственное положение векторов.
Xan>> И на ней, В ЛЮБОЙ УДОБНОЙ ДЛЯ РАСЧЁТОВ ТОЧКЕ, прикладываешь силу тяги.
Xan>> Правый рисунок (как частный случай) правильный.
Massaraksh> Спасибо. Но за счет чего ракета повернется? Если я просто посчитаю результирующую силу, к какой точке я её должен применить?
На правом рисунке из ЦТ опускаешь перпендикуляр на линию тяги.
Длина перпендикуляра — плечо, тяга — сила:
Момент_Силы = Длина_Плеча * Величину_Силы
Раз к ракете приложен момент, она будет вращаться с ускорением:
Ускорение_Вращения = Момент_Силы / Момент_Инерции
=====
В общем случае момент считается так (см. картинку):
Берётся произвольная точка O в пространстве, всё равно, внутри или вне ракеты;
Берётся радиусвектор из этой точки к центру масс — R0;
Берётся вектор тяги со знаком минус (-F = m * a) и векторно умножается на R0;
Проводится радиусвектор из точки O в произвольную точку на оси сопла (оси/линии тяги);
На рисунке два варианта: R1 и R2
Вектор тяги со знаком плюс умножается на этот вектор;
Сумма произведений — это и есть момент, действующий на ракету.
И результат не зависит от выбора точки O.
И поэтому её имеет смысл выбирать в хорошем месте.
Например, в центре масс, тогда R0 = 0 и не надо считать одно из векторных произведений.
И точку на оси тяги тоже надо выбирать хорошую.
Например, опустив перпендикуляр из ЦМ на эту линию. Тогда модуль векторного произведения считается легко.
И задача сведена к тому, что написано в самом начале поста.
Xan>> Правый рисунок (как частный случай) правильный.
Massaraksh> Спасибо. Но за счет чего ракета повернется? Если я просто посчитаю результирующую силу, к какой точке я её должен применить?
На правом рисунке из ЦТ опускаешь перпендикуляр на линию тяги.
Длина перпендикуляра — плечо, тяга — сила:
Момент_Силы = Длина_Плеча * Величину_Силы
Раз к ракете приложен момент, она будет вращаться с ускорением:
Ускорение_Вращения = Момент_Силы / Момент_Инерции
=====
В общем случае момент считается так (см. картинку):
Берётся произвольная точка O в пространстве, всё равно, внутри или вне ракеты;
Берётся радиусвектор из этой точки к центру масс — R0;
Берётся вектор тяги со знаком минус (-F = m * a) и векторно умножается на R0;
Проводится радиусвектор из точки O в произвольную точку на оси сопла (оси/линии тяги);
На рисунке два варианта: R1 и R2
Вектор тяги со знаком плюс умножается на этот вектор;
Сумма произведений — это и есть момент, действующий на ракету.
И результат не зависит от выбора точки O.
И поэтому её имеет смысл выбирать в хорошем месте.
Например, в центре масс, тогда R0 = 0 и не надо считать одно из векторных произведений.
И точку на оси тяги тоже надо выбирать хорошую.
Например, опустив перпендикуляр из ЦМ на эту линию. Тогда модуль векторного произведения считается легко.
И задача сведена к тому, что написано в самом начале поста.
Прикреплённые файлы:
- Xan [06.02.2018 16:14]: Перенос сообщений в Споры с SashaPro
- Xan [06.02.2018 16:40]: Перенос сообщений в Споры с SashaPro
Massaraksh> Хочу смоделировать движение ракеты в упрощённом виде, исходя из двух сил: тяги и силы тяжести.
Сила тяжести вообще не при чем, она всегда через ЦТ. Просто её проекция на вектор тяги будет вычитаться.
Massaraksh> Если на левом рисунке, то за счет чего ракета будет поворачиваться?
На левом рисунке ракета поворачиваться не будет, если нет других сил.
Massaraksh> Если на правом рисунке, то как считается результирующая(ие) сила(ы)?
На правом рисунке ситуация сложная. Поступательное движение будет за счет проекции тяги на ось ракеты минус тяжесть, плюс вращательное движение за счет момента от тяги на плече из ЦТ перпендикулярном вектору тяги.
Сила тяжести вообще не при чем, она всегда через ЦТ. Просто её проекция на вектор тяги будет вычитаться.
Massaraksh> Если на левом рисунке, то за счет чего ракета будет поворачиваться?
На левом рисунке ракета поворачиваться не будет, если нет других сил.
Massaraksh> Если на правом рисунке, то как считается результирующая(ие) сила(ы)?
На правом рисунке ситуация сложная. Поступательное движение будет за счет проекции тяги на ось ракеты минус тяжесть, плюс вращательное движение за счет момента от тяги на плече из ЦТ перпендикулярном вектору тяги.
RocKI> На правом рисунке ситуация сложная. Поступательное движение будет за счет проекции тяги на ось ракеты минус тяжесть, плюс вращательное движение за счет момента от тяги на плече из ЦТ перпендикулярном вектору тяги.
Ну, собственно, именно это я и хочу смоделировать, сначала в 2D, потом в 3D.
Ладно, всем спасибо, направление мыслей мне задали, дальше буду разбираться сам.
Ну, собственно, именно это я и хочу смоделировать, сначала в 2D, потом в 3D.
Ладно, всем спасибо, направление мыслей мне задали, дальше буду разбираться сам.
Massaraksh> Ладно, всем спасибо, направление мыслей мне задали, дальше буду разбираться сам.
Собсна, всё очень просто:
Сумма всех сил (гравитация, воздух, тяга) / массу;
Сумма всех моментов / момент инерции.
Вот тебе и оба ускорения.
Собсна, всё очень просто:
Сумма всех сил (гравитация, воздух, тяга) / массу;
Сумма всех моментов / момент инерции.
Вот тебе и оба ускорения.
Моделирование в 2D получилось. Но сделал по-своему, как я понял. Через силы, без моментов инерции. Потом попробую в 3D, а дальше будем пробовать моделировать управление.
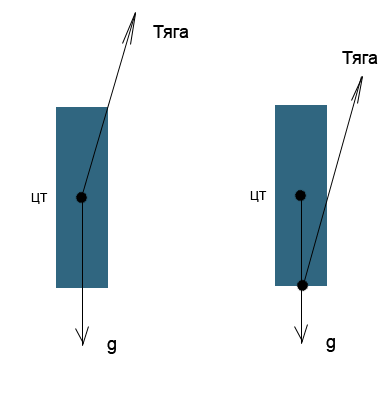
Движение тела под действием 2 сил.
Моделирование движения тела под действием силы тяжести и тяги, направленной под углом +-alfa к точке тела.
Движение тела под действием 2 сил.
Моделирование движения тела под действием силы тяжести и тяги, направленной под углом +-alfa к точке тела.
Это сообщение редактировалось 08.02.2018 в 16:35
Massaraksh> Моделирование в 2D получилось.
Похоже на правду!
Похоже на правду!
Xan> Похоже на правду!
Кстати, только после этого моделирования понял, зачем гироскопы выдают угловую скорость. Это удобно для управления.
Кстати, только после этого моделирования понял, зачем гироскопы выдают угловую скорость. Это удобно для управления.
Ну и поуправлять в полуавтомате.
И небольшая иллюстрация, как это считалось, если кому нужно будет.
Прикреплённые файлы:
Massaraksh> И небольшая иллюстрация, как это считалось, если кому нужно будет.
Вроде все верно, но ума не приложу, как ты обошелся без момента инерции.
Вроде все верно, но ума не приложу, как ты обошелся без момента инерции.
RocKI> Вроде все верно, но ума не приложу, как ты обошелся без момента инерции.
Просто поставил некую константу.
Просто поставил некую константу.
Mikhal
втянувшийся
Доброго дня! Вопрос такой - какой железоокисный пигмент в карамельное топливо предпочтительнее? Я понял, что коричневый, потому что он максимально увеличивает скорость горения до максимальных (100 атм) давлений в отличие от красного и жёлтого (30 атм). Есть разные модификации коричневого:
510; 520; 610; 663; 686; 868. Содержание оксида железа в них 91-93%. Есть ли разница? Или следует искать какой-нибудь другой с 98%?
510; 520; 610; 663; 686; 868. Содержание оксида железа в них 91-93%. Есть ли разница? Или следует искать какой-нибудь другой с 98%?
Mikhal> он максимально увеличивает скорость горения до максимальных (100 атм) давлений в отличие от красного и жёлтого (30 атм)
Как-то странно ты оцениваешь скорость горения - в атмосферах.
Как-то странно ты оцениваешь скорость горения - в атмосферах.
Mikhal
втянувшийся
RocKI> Как-то странно ты оцениваешь скорость горения - в атмосферах.
В атмосферах - давление, при котором катализатор увеличивает скорость горения.
В атмосферах - давление, при котором катализатор увеличивает скорость горения.
Mikhal> В атмосферах - давление, при котором катализатор увеличивает скорость горения.
Ну, ты все-таки отделяй мухи от котлет. Корректно сравнивать скорость горения в мм/с при одинаковом давлении.
Ну, ты все-таки отделяй мухи от котлет. Корректно сравнивать скорость горения в мм/с при одинаковом давлении.
Реклама Google — средство выживания форумов :)
Mikhal> до максимальных (100 атм) давлений в отличие от красного и жёлтого (30 атм). Есть разные модификации коричневого:
Про давление все правильно.
Про коричневый оксид, это для меня загадка.
Mikhal> 510; 520; 610; 663; 686; 868.
А можно информацию где ты это все нашел?
Про давление все правильно.
Про коричневый оксид, это для меня загадка.
Mikhal> 510; 520; 610; 663; 686; 868.
А можно информацию где ты это все нашел?
Copyright © Balancer 1997..2023
Создано 27.05.2017
Связь с владельцами и администрацией сайта: anonisimov@gmail.com, rwasp1957@yandex.ru и admin@balancer.ru.
Создано 27.05.2017
Связь с владельцами и администрацией сайта: anonisimov@gmail.com, rwasp1957@yandex.ru и admin@balancer.ru.
