-
![[image]](https://www.balancer.ru/cache/sites/ru/zv/zveronline/adsl/projects/articles/2008/08/26/kadry_kotorye_potryasli_mir_1/128x128-crop/b076ca54.jpg)
Звездолет комбинированной схемы работы
Вперед на Электра - подборка тяжёлого бредаТеги:
A.s.> Поэтому МОСКВА -Кассиопея (дура ты, баба!). Не Земля.
Да явная пасхалка, скрытое цитирование.
Герои и смельчаки проложат первые тропы трасс: Земля — орбита Луны, Земля — орбита Марса и еще далее: Москва — Луна, Калуга — Марс.
(хотя, кажется, есть несколько редакций, ЕМНИС, в одной из них "Земля - Луна, Калуга - Марс")
И помимо (еле) скрытой отсылки к истокам, "Москва - Кассиопея" банально звучит лучше, чем "Земля - Кассиопея", чиста по ритму.
Да явная пасхалка, скрытое цитирование.
Герои и смельчаки проложат первые тропы трасс: Земля — орбита Луны, Земля — орбита Марса и еще далее: Москва — Луна, Калуга — Марс.
(хотя, кажется, есть несколько редакций, ЕМНИС, в одной из них "Земля - Луна, Калуга - Марс")
И помимо (еле) скрытой отсылки к истокам, "Москва - Кассиопея" банально звучит лучше, чем "Земля - Кассиопея", чиста по ритму.


Полл>> 15-летний капитан был нормой в эпоху Колумба.
Fakir> Как насчёт примера? Хоть одного, и уж тем более что это была норма ?
Fakir> Капитан именно солидного судна, а не тартаны или там рыбацкого карбаса.
Френсис Дрейк сойдёт?
Родился где-то в промежуток 1539-1544, в 1561 стал шкипером, то есть капитаном.
Кстати, его крёстным отцом стал человек, родившийся в 1527 году.
Fakir> А вот это уже точно можно считать распространённым заблуждением. Когда сейчас историки докапываются до кучи документальных свидетельств европейского средневековья, то выясняется, что, к примеру, для горожанок было нормой
Горожан в средневековье было менее 1% населения.
То, что было нормой среди горожан, к нормам средневекового общества не относится никак.
Fakir> Основные забросы вниз по брачному возрасту были у крестьян (рабочие руки нужны) и у дворянства, да чаще не самого мелкого (нужны бабки, земли и породниться поскорей с кем надо). При этом часто эти ранние браки по нескольку лет оставались "бумажными" и не консумировались отправлением супружеских обязанностей, жена могла даже продолжать жить у своих родителей.
Да, ты только не забывай уточнить, что ранние браки в терминах тех лет это браки детей ранее 10 лет.
Fakir> Равно как и 31-летняя женщина как минимум среди горожан (и ремесленных, и дворян) старухой отнюдь не считалась. Женщина за жизнь - если доживала до 30+, не умирая от родов - часто вдовела,
Женщины старше 30 в средневековье были редкостью, и чаще всего бесплодными.
Умирали до 30 - более 90%.
Fakir> Скорее, экономия ресурсов за счёт реализации относительных страновых преимуществ (всё по дедушке Рикардо) в условиях резкого снижения транспортных издержек
Я напомню, что бюджет США на оборону за прошлый год - 738 млрд, а бюджет НАСА - 21 млрд.
Fakir> Как насчёт примера? Хоть одного, и уж тем более что это была норма ?
Fakir> Капитан именно солидного судна, а не тартаны или там рыбацкого карбаса.
Френсис Дрейк сойдёт?
Родился где-то в промежуток 1539-1544, в 1561 стал шкипером, то есть капитаном.
Кстати, его крёстным отцом стал человек, родившийся в 1527 году.
Fakir> А вот это уже точно можно считать распространённым заблуждением. Когда сейчас историки докапываются до кучи документальных свидетельств европейского средневековья, то выясняется, что, к примеру, для горожанок было нормой
Горожан в средневековье было менее 1% населения.
То, что было нормой среди горожан, к нормам средневекового общества не относится никак.
Fakir> Основные забросы вниз по брачному возрасту были у крестьян (рабочие руки нужны) и у дворянства, да чаще не самого мелкого (нужны бабки, земли и породниться поскорей с кем надо). При этом часто эти ранние браки по нескольку лет оставались "бумажными" и не консумировались отправлением супружеских обязанностей, жена могла даже продолжать жить у своих родителей.
Да, ты только не забывай уточнить, что ранние браки в терминах тех лет это браки детей ранее 10 лет.
Fakir> Равно как и 31-летняя женщина как минимум среди горожан (и ремесленных, и дворян) старухой отнюдь не считалась. Женщина за жизнь - если доживала до 30+, не умирая от родов - часто вдовела,
Женщины старше 30 в средневековье были редкостью, и чаще всего бесплодными.
Умирали до 30 - более 90%.
Fakir> Скорее, экономия ресурсов за счёт реализации относительных страновых преимуществ (всё по дедушке Рикардо) в условиях резкого снижения транспортных издержек
Я напомню, что бюджет США на оборону за прошлый год - 738 млрд, а бюджет НАСА - 21 млрд.


Полл>>> 15-летний капитан был нормой в эпоху Колумба.
Fakir>> Как насчёт примера? Хоть одного, и уж тем более что это была норма ?
Fakir>> Капитан именно солидного судна, а не тартаны или там рыбацкого карбаса.
Полл> Френсис Дрейк сойдёт?
Полл> Родился где-то в промежуток 1539-1544, в 1561 стал шкипером, то есть капитаном.
Арифметика подсказывает нам, что шкипером он стал в возрасте от 17 до 22 лет, а логика - что, вероятнее всего, в 20-22.
Полл> Горожан в средневековье было менее 1% населения.
Кто тебе это сказал, и почему ты ему поверил?
Полл> То, что было нормой среди горожан, к нормам средневекового общества не относится никак.
По сельскому населению документов меньше. Хотя в Англии с церковными книгами картина получше, и там нет особо радикальной разницы между городом и деревней.
Полл> Да, ты только не забывай уточнить, что ранние браки в терминах тех лет это браки детей ранее 10 лет.
12 и даже до 14 могли быть аналогично.
Полл> Женщины старше 30 в средневековье были редкостью, и чаще всего бесплодными.
Заблуждение.
Полл> Умирали до 30 - более 90%.
Цифра сама по себе весьма сомнительна.
И из тех, кто дожил до совершеннолетия (брачного возраста, если угодно) далее до 30 доживало едва ли меньше половины.
Полл> Я напомню, что бюджет США на оборону за прошлый год - 738 млрд, а бюджет НАСА - 21 млрд.
Казалось бы, причём тутЛужков глобализация?
Fakir>> Как насчёт примера? Хоть одного, и уж тем более что это была норма ?
Fakir>> Капитан именно солидного судна, а не тартаны или там рыбацкого карбаса.
Полл> Френсис Дрейк сойдёт?
Полл> Родился где-то в промежуток 1539-1544, в 1561 стал шкипером, то есть капитаном.
Арифметика подсказывает нам, что шкипером он стал в возрасте от 17 до 22 лет, а логика - что, вероятнее всего, в 20-22.
Полл> Горожан в средневековье было менее 1% населения.
Кто тебе это сказал, и почему ты ему поверил?
Полл> То, что было нормой среди горожан, к нормам средневекового общества не относится никак.
По сельскому населению документов меньше. Хотя в Англии с церковными книгами картина получше, и там нет особо радикальной разницы между городом и деревней.
Полл> Да, ты только не забывай уточнить, что ранние браки в терминах тех лет это браки детей ранее 10 лет.
12 и даже до 14 могли быть аналогично.
Полл> Женщины старше 30 в средневековье были редкостью, и чаще всего бесплодными.
Заблуждение.
Полл> Умирали до 30 - более 90%.
Цифра сама по себе весьма сомнительна.
И из тех, кто дожил до совершеннолетия (брачного возраста, если угодно) далее до 30 доживало едва ли меньше половины.
Полл> Я напомню, что бюджет США на оборону за прошлый год - 738 млрд, а бюджет НАСА - 21 млрд.
Казалось бы, причём тут


Fakir> Арифметика подсказывает нам, что шкипером он стал в возрасте от 17 до 22 лет, а логика - что, вероятнее всего, в 20-22.
Вообще арифметика говорит нам, что капитаном Дрейк стал в возрасте от 16 до 22, а логика говорит, что звать в крестные отцы человека 13-14 лет - рановато даже по меркам средневековья. Особенно по меркам Средневековья, когда значение Крестного отца было намного выше нынешнего.
Полл>> Горожан в средневековье было менее 1% населения.
Fakir> Кто тебе это сказал, и почему ты ему поверил?
К примеру, тут:

Численность населения всех городов крупнее 10 000 человек на 1550 год - менее 6% от общего населения Европы.
При этом в эти 6% попадают и крестьяне, которых в средневековых города от трети до двух третей населения.
Fakir> По сельскому населению документов меньше. Хотя в Англии с церковными книгами картина получше, и там нет особо радикальной разницы между городом и деревней.
Да, нет там особой разницы. Демография средневековья изучена довольно хорошо, и средняя, и медианные продолжительности жизни по каждому периоду известны.
Fakir> 12 и даже до 14 могли быть аналогично.
И даже в 30 лет такие браки известны.
Единичные.
Fakir> И из тех, кто дожил до совершеннолетия (брачного возраста, если угодно) далее до 30 доживало едва ли меньше половины.
Буду рад ознакомиться с научным трудом, содержащим столь интересные данные.
Вообще арифметика говорит нам, что капитаном Дрейк стал в возрасте от 16 до 22, а логика говорит, что звать в крестные отцы человека 13-14 лет - рановато даже по меркам средневековья. Особенно по меркам Средневековья, когда значение Крестного отца было намного выше нынешнего.
Полл>> Горожан в средневековье было менее 1% населения.
Fakir> Кто тебе это сказал, и почему ты ему поверил?
К примеру, тут:

Демографическая история Европы
Идет строительство Европы. С этим связываются большие надежды. Их удастся реализовать только учитывая исторический опыт: ведь Европа без истории была бы подобна дереву без корней. День сегодняшний начался вчера, будущее всегда обусловлено прошлым. Прошлое не должно связывать руки настоящему, но может помочь ему развиваться, сохраняя верность традициям, и создавать новое, продвигаясь вперед по пути прогресса. Наша Европа, территория, расположенная между Атлантикой, Азией и Африкой, существует с давнего времени: ее пределы определены географией, а нынешний облик формировался под воздействием истории — с тех самых пор, как греки дали ей имя, оставшееся неизменным до наших дней. // Дальше — www.universalinternetlibrary.ruЧисленность населения всех городов крупнее 10 000 человек на 1550 год - менее 6% от общего населения Европы.
При этом в эти 6% попадают и крестьяне, которых в средневековых города от трети до двух третей населения.
Fakir> По сельскому населению документов меньше. Хотя в Англии с церковными книгами картина получше, и там нет особо радикальной разницы между городом и деревней.
Да, нет там особой разницы. Демография средневековья изучена довольно хорошо, и средняя, и медианные продолжительности жизни по каждому периоду известны.
Fakir> 12 и даже до 14 могли быть аналогично.
И даже в 30 лет такие браки известны.
Единичные.
Fakir> И из тех, кто дожил до совершеннолетия (брачного возраста, если угодно) далее до 30 доживало едва ли меньше половины.
Буду рад ознакомиться с научным трудом, содержащим столь интересные данные.


Это сообщение редактировалось 29.12.2021 в 19:32
Полл> С экономической точки зрения глобализация это высвобождение на полезную деятельность огромных ресурсов, которые сегодня утилизируются в армию, спецслужбы и ВПК.
Тьфу на вас, Пол!
Даже отвечать не стану!
Бердятина (ложь) заезженная. Скучная до оскомины. Как плямканье Брежнева на XXV съезде КПСС! Ей богу!

Тьфу на вас, Пол!
Даже отвечать не стану!
Бердятина (ложь) заезженная. Скучная до оскомины. Как плямканье Брежнева на XXV съезде КПСС! Ей богу!



Fakir> И помимо (еле) скрытой отсылки к истокам, "Москва - Кассиопея" банально звучит лучше, чем "Земля - Кассиопея", чиста по ритму.
Смысл "СССР-Кассиопея", мол нас рать на мировое сообщество, сами - с усами. Вы на Луну? А мы на Кассиопею! (именно "на"!) Такой месседж читался ТОГДА (я же помню)!
Такой месседж читался ТОГДА (я же помню)!
Но "СССР" - не звучит, и вообще слишком прямо... "Москва"- лучше всего. "Москва, Кремль,Сталин Путин"... Звучит? Звучит, черт побери!!! Продукция нашего завода звучит! ("Чародеи").

Кстати "ЗАРЯ" Звездолет, Атомный, Релятивистский, Ядерный.. Так было написано и на борту первой орбитальной станции. Которая по сути переделанный "Алмаз" а официально "Салют":

Так что ЗАРЯ... очень даже современно было. Да, притянутый за уши набор вроде как подходящих слов в расшифровке.
Ну а если вы посмотрите режиссерский сценарий то там звездолет назывался... "ЗАЛП". Милитаристски как-то.
Звездолет Анигиляционный, Лазерный... ПРЯМОТОЧНЫЙ!
И на картинках в презентации у Вити Середы (кстати в в ролике у этой девицы это тоже отмечено- умница, откопала) - схем анигиляции из книги Бурдакова 1969го года к его "прямоточке" с которой он с 1963-го года носился очень долго!
Зря они боевой ЗАЛП отменили! Переименовали в мирную ЗАРЮ.
Лазерны тут явно за уши притянуто в расшифровке. А анигиляция и прямоточка - это бурдаковский псевдорелаизЬм... Сказка то сказка... Но вон Камерон к такому ПСЕВДОреализЬму только вот-вот пришел...
Вот как должен был выглядеть ЗАЛП по идее...
Для сказки очень круто! Зря они тут смазали. Играться в песочнице? Так по-взрослому!

Смысл "СССР-Кассиопея", мол нас рать на мировое сообщество, сами - с усами. Вы на Луну? А мы на Кассиопею! (именно "на"!)
 Такой месседж читался ТОГДА (я же помню)!
Такой месседж читался ТОГДА (я же помню)!Но "СССР" - не звучит, и вообще слишком прямо... "Москва"- лучше всего. "Москва, Кремль,

Кстати "ЗАРЯ" Звездолет, Атомный, Релятивистский, Ядерный.. Так было написано и на борту первой орбитальной станции. Которая по сути переделанный "Алмаз" а официально "Салют":

Так что ЗАРЯ... очень даже современно было. Да, притянутый за уши набор вроде как подходящих слов в расшифровке.
Ну а если вы посмотрите режиссерский сценарий то там звездолет назывался... "ЗАЛП". Милитаристски как-то.
Звездолет Анигиляционный, Лазерный... ПРЯМОТОЧНЫЙ!
И на картинках в презентации у Вити Середы (кстати в в ролике у этой девицы это тоже отмечено- умница, откопала) - схем анигиляции из книги Бурдакова 1969го года к его "прямоточке" с которой он с 1963-го года носился очень долго!
Зря они боевой ЗАЛП отменили! Переименовали в мирную ЗАРЮ.
Лазерны тут явно за уши притянуто в расшифровке. А анигиляция и прямоточка - это бурдаковский псевдорелаизЬм... Сказка то сказка... Но вон Камерон к такому ПСЕВДОреализЬму только вот-вот пришел...
Вот как должен был выглядеть ЗАЛП по идее...
Для сказки очень круто! Зря они тут смазали. Играться в песочнице? Так по-взрослому!



Это сообщение редактировалось 30.12.2021 в 17:07
A.s.> И на картинках в презентации у Вити Середы (кстати в в ролике у этой девицы это тоже отмечено- умница, откопала) - схем анигиляции из книги Бурдакова 1969го года к его "прямоточке" с которой он с 1963-го года носился очень долго!
Я поражаюсь, как вы умудряетесь мелочи не замечать
Я поражаюсь, как вы умудряетесь мелочи не замечать



--
Прикреплённые файлы:


PSS> Мне было интересно что современный кинокритик скажет про этот фильм. Я и притащил как схему прямоточника, так и некоторые другие материалы. К сожалению, взяла только схему.
Блин... а я как всегда "поверил в чудо"

PSS> Я поражаюсь, как вы умудряетесь мелочи не замечать
Титры в конце, как правило уже не смотрю. Но да...
В общем, ваши критики "тему сисек не раскрыли".
Блин... а я как всегда "поверил в чудо"

PSS> Я поражаюсь, как вы умудряетесь мелочи не замечать

Титры в конце, как правило уже не смотрю. Но да...
В общем, ваши критики "тему сисек не раскрыли".


Fakir> Да явная пасхалка, скрытое цитирование.
Fakir> Герои и смельчаки проложат первые тропы трасс: Земля — орбита Луны, Земля — орбита Марса и еще далее: Москва — Луна, Калуга — Марс.
Да, и еще одна, более тонкая пасхалка:
"...из Москвы - в Нагасаки, из Нью-Йорка - на Марс!"
© Игорь Северянин
Fakir> Герои и смельчаки проложат первые тропы трасс: Земля — орбита Луны, Земля — орбита Марса и еще далее: Москва — Луна, Калуга — Марс.
Да, и еще одна, более тонкая пасхалка:
"...из Москвы - в Нагасаки, из Нью-Йорка - на Марс!"

© Игорь Северянин


Сообщение было перенесено из темы Прецизионный одноступенчатый ядерный заряд мощностью до 1 Ктн. Новая надежда Америки?.
PSS> Датчики Цезаря/СОСУС и на глубине в километры находились.
Павел.
Не знаю как вас иначе привлечь.
Вам всё еще интересна задача об оптимизации параметров и траектории межзвездной ракеты?
Помните это?
Вы интересовались одно время.
Вот по-сути полное ее решение (тут есть некоторые ляпы в оформлении, выборе символики но в целом всё верно):

Мы на Астрофоруме таки ДОМУЧАЛИ эту тему.
Несколько человек разными путями сошлись к одном по-сути результату.
Вот развитие этого же от другого более образованного чем я участника форума (захотел остаться инкогнито):

Задача оказалась гораздо интересней. Частный случай с постоянно включенным двигателем, оказался не самый оптимальный. На самом деле оптимальная одноступенчатая межзвездная ракета требует определенного инерционного участка, который надо тоже искать как оптимум. То есть оптимизация уже по двум параметрам, скорости истечения и формы траектории. Аналитически эта оптимизация уже не решается и я сразу набросал, а сегодня уже допилил до "товарного образца" и электронную таблицу в Excel, которая решает эту задачу. См. приложенный скриншёт с этой таблицы.
Если вам всё еще интересно, я дам вам ссылку где это можно всё подробно почитать и скачать мою таблицу. Там придётся поморочиться что бы включить "поиск решения" в макросах (в разных версиях Excel, разного выпуска, библиотеки к макросам не подходят и что бы у вас работала правильная библиотека, надо там чуть-чуть допилить себе в настройках)
Павел.
Не знаю как вас иначе привлечь.
Вам всё еще интересна задача об оптимизации параметров и траектории межзвездной ракеты?
Помните это?
Вы интересовались одно время.
Вот по-сути полное ее решение (тут есть некоторые ляпы в оформлении, выборе символики но в целом всё верно):
Мы на Астрофоруме таки ДОМУЧАЛИ эту тему.
Несколько человек разными путями сошлись к одном по-сути результату.
Вот развитие этого же от другого более образованного чем я участника форума (захотел остаться инкогнито):
Задача оказалась гораздо интересней. Частный случай с постоянно включенным двигателем, оказался не самый оптимальный. На самом деле оптимальная одноступенчатая межзвездная ракета требует определенного инерционного участка, который надо тоже искать как оптимум. То есть оптимизация уже по двум параметрам, скорости истечения и формы траектории. Аналитически эта оптимизация уже не решается и я сразу набросал, а сегодня уже допилил до "товарного образца" и электронную таблицу в Excel, которая решает эту задачу. См. приложенный скриншёт с этой таблицы.
Если вам всё еще интересно, я дам вам ссылку где это можно всё подробно почитать и скачать мою таблицу. Там придётся поморочиться что бы включить "поиск решения" в макросах (в разных версиях Excel, разного выпуска, библиотеки к макросам не подходят и что бы у вас работала правильная библиотека, надо там чуть-чуть допилить себе в настройках)
Прикреплённые файлы:


PSS>> Датчики Цезаря/СОСУС и на глубине в километры находились.
A.s.> Павел.
A.s.> Не знаю как вас иначе привлечь.
A.s.> Вам всё еще интересна задача об оптимизации параметров и траектории межзвездной ракеты?
Добрый день! Спасибо. На самом деле нужно поднять мои расчеты и опубликовать. То, что нужен инерционный момент это очевидно. Об этом я кажется писал. Причем чем больше, тем лучше.
A.s.> Павел.
A.s.> Не знаю как вас иначе привлечь.
A.s.> Вам всё еще интересна задача об оптимизации параметров и траектории межзвездной ракеты?
Добрый день! Спасибо. На самом деле нужно поднять мои расчеты и опубликовать. То, что нужен инерционный момент это очевидно. Об этом я кажется писал. Причем чем больше, тем лучше.


PSS>> Датчики Цезаря/СОСУС и на глубине в километры находились.
A.s.> Павел.
Вот мой текст

Обратите внимание на Вашу формулу 16 и мою последнюю формулу.
A.s.> Павел.
Вот мой текст

Звездолет комбинированной схемы работы [PSS#23.03.20 19:36]
https://astronomy.ru/forum/index .php?action=dlattach;topic=11251 7.0;attach=574945;image Алекс.. Надеюсь Вы это читаете. Дело в том, что я все таки решил задачу полета звездолета с постоянной тягой и удельным импульсом. Именно тягой, не ускорением. Сначала занялся от скуки в поезде, а теперь и карантин подоспел. Результат получился настолько парадоксальным, что я его несколько раз проверил на численных моделях и они подтвердили верность аналитической формулы. В целом даже понял геометрический…// Чёрная дыраОбратите внимание на Вашу формулу 16 и мою последнюю формулу.


PSS>>> Датчики Цезаря/СОСУС и на глубине в километры находились.
A.s.>> Павел.
PSS> Вот мой текст
PSS> Обратите внимание на Вашу формулу 16 и мою последнюю формулу.
Смотрю.
Ищу знакомые буквы. Я и раньше смотрел. И сейчас и раньше я вижу что вы решаете (вроде верно решаете) другую (чуть) задачу. Похожую но другую.
Я и раньше смотрел. И сейчас и раньше я вижу что вы решаете (вроде верно решаете) другую (чуть) задачу. Похожую но другую.
Кстати, ценный "листочек" тоже.
Я бы вас "взял бы в нашу команду". Чем больше людей приходят к сумме хороших близких решений, тем лучше! Мы же, хоть и коротышки, но одно дело делаем?


Но тут вы зная сразу такие параметры ракеты как F - тяга, M - начальная масса, m - коненчная (то есть вы уже знаете R - число Циолковского, R=M/m) и u - скорость истечения рабочего тела, вы высчитываете дистанцию L на которой ракета разгонится до некоторой пиковой скорости v (ее вы тоже узнаёте), а потом затормозится до нуля (не двигаясь по инерции).
Главное отличие моего уравнения (16) от последней вашей формулы. Вы находите там дистанцию. А у меня дистанция - исходный параметр. Я ищу у себя время T.
Да, вы тоже находите суммарное время там выше. НО!
Вы не тот набор исходных параметров задаете изначально что мы.
То есть вы находите тут во всём этом своём решении [T, L, v]= f (F, M, m, u), или, если не привязываться к конкретной массе ракеты [T, L,v]= f(F/m, R, u) при условии что ракета разгоняется и сразу же тормозит.
Моё "программистское" обозначение тут [T, L, v] - означает что f это "процедура", система уравнений которые дают не только общее время T, но и дистанцию L (даже дистанции разгона и торможения) и пиковую скорость. Три параметра. То есть обозначение f - это не просто выражение, это несколько взаимосвязанных выражений для каждого перечисленного в квадратных скобках. То есть связанное решение.
Решение у вас может и верное и пересекается с нашим. Но мы же искали несколько иное.
Во первых мы использовали не тягу (удельную тягу), а удельную мощность. Но это не принципиальное отличие, не суть. W=Fu/2 - полезная мощность ракеты равна половине тяги на скорость истечения. То есть удельная мощность w - половина удельной тяги F/m на скорость истечения. В вашей и нашей задаче удельную тягу легко поменять на удельную мощность. Они взаимозаменяемы. Поэтому тут - не суть. И если так то наша задача (в ваших терминах) и решение выглядит так:
[T, v, R] = f'(F/m, L, u) или в наших терминах: [T, v, R] = f'(w, L, u)
Но обратите внимание на принципиальное отличие. Дистанцию мы не находим. Мы ее задаём как исходную данность (в отличии от вашего решения). Зато мы не знаем изначально R, то есть по-сути начальную и конечную массу. Мы не знаем какие они, мы их находим в процессе решения, найдя R. Зная лишь удельную мощность (или удельную тягу) дистанцию и скорость истечения. Находим время, пиковую скорость v и R. Разумеется, находим потом и отдельно дистанцию разгона и дистанцию торможения (как исходная L делится на разгон и торможение, в какой пропорции). Но это - боковые ветки решения.
Главное к чему мы рвёмся - время T. По нему потом и ищется оптимум.
То есть сама постановка задачи - другая.
В частности выражение (16) по суть T= f'16(L, w, u). Мы тут не знаем начальную и конечную массу ракеты, не знаем числа Циолковского. Оно "спрятано" в L, w и u - наши исходные данные. А в вашем решении надо знать начальную и конечную массу (либо R, не суть) с самого начала. А L у вас - свободный параметр, вы его и вычисляете. Ибо всё ваше решение и начинается с того что вы знаете массы (R) но не знаете L. А мы знаем L, но не знаем R.
То есть вы тут решили чуть другую задачу. Похожую. Но другую.

A.s.>> Павел.
PSS> Вот мой текст
PSS> Обратите внимание на Вашу формулу 16 и мою последнюю формулу.
Смотрю.
Ищу знакомые буквы.
 Я и раньше смотрел. И сейчас и раньше я вижу что вы решаете (вроде верно решаете) другую (чуть) задачу. Похожую но другую.
Я и раньше смотрел. И сейчас и раньше я вижу что вы решаете (вроде верно решаете) другую (чуть) задачу. Похожую но другую.Кстати, ценный "листочек" тоже.
Я бы вас "взял бы в нашу команду". Чем больше людей приходят к сумме хороших близких решений, тем лучше! Мы же, хоть и коротышки, но одно дело делаем?

Но тут вы зная сразу такие параметры ракеты как F - тяга, M - начальная масса, m - коненчная (то есть вы уже знаете R - число Циолковского, R=M/m) и u - скорость истечения рабочего тела, вы высчитываете дистанцию L на которой ракета разгонится до некоторой пиковой скорости v (ее вы тоже узнаёте), а потом затормозится до нуля (не двигаясь по инерции).
Главное отличие моего уравнения (16) от последней вашей формулы. Вы находите там дистанцию. А у меня дистанция - исходный параметр. Я ищу у себя время T.
Да, вы тоже находите суммарное время там выше. НО!
Вы не тот набор исходных параметров задаете изначально что мы.
То есть вы находите тут во всём этом своём решении [T, L, v]= f (F, M, m, u), или, если не привязываться к конкретной массе ракеты [T, L,v]= f(F/m, R, u) при условии что ракета разгоняется и сразу же тормозит.
Моё "программистское" обозначение тут [T, L, v] - означает что f это "процедура", система уравнений которые дают не только общее время T, но и дистанцию L (даже дистанции разгона и торможения) и пиковую скорость. Три параметра. То есть обозначение f - это не просто выражение, это несколько взаимосвязанных выражений для каждого перечисленного в квадратных скобках. То есть связанное решение.
Решение у вас может и верное и пересекается с нашим. Но мы же искали несколько иное.
Во первых мы использовали не тягу (удельную тягу), а удельную мощность. Но это не принципиальное отличие, не суть. W=Fu/2 - полезная мощность ракеты равна половине тяги на скорость истечения. То есть удельная мощность w - половина удельной тяги F/m на скорость истечения. В вашей и нашей задаче удельную тягу легко поменять на удельную мощность. Они взаимозаменяемы. Поэтому тут - не суть. И если так то наша задача (в ваших терминах) и решение выглядит так:
[T, v, R] = f'(F/m, L, u) или в наших терминах: [T, v, R] = f'(w, L, u)
Но обратите внимание на принципиальное отличие. Дистанцию мы не находим. Мы ее задаём как исходную данность (в отличии от вашего решения). Зато мы не знаем изначально R, то есть по-сути начальную и конечную массу. Мы не знаем какие они, мы их находим в процессе решения, найдя R. Зная лишь удельную мощность (или удельную тягу) дистанцию и скорость истечения. Находим время, пиковую скорость v и R. Разумеется, находим потом и отдельно дистанцию разгона и дистанцию торможения (как исходная L делится на разгон и торможение, в какой пропорции). Но это - боковые ветки решения.
Главное к чему мы рвёмся - время T. По нему потом и ищется оптимум.
То есть сама постановка задачи - другая.
В частности выражение (16) по суть T= f'16(L, w, u). Мы тут не знаем начальную и конечную массу ракеты, не знаем числа Циолковского. Оно "спрятано" в L, w и u - наши исходные данные. А в вашем решении надо знать начальную и конечную массу (либо R, не суть) с самого начала. А L у вас - свободный параметр, вы его и вычисляете. Ибо всё ваше решение и начинается с того что вы знаете массы (R) но не знаете L. А мы знаем L, но не знаем R.
То есть вы тут решили чуть другую задачу. Похожую. Но другую.



Это сообщение редактировалось 21.01.2023 в 16:02
- Fakir [21.01.2023 15:53]: Перенос сообщений из Прецизионный одноступенчатый ядерный заряд мощностью до 1 Ктн. Новая надежда Америки?
Есть ещё такой Иван Моисеев, предвадитель уездного дворянства директор некого (общественного) института космической политики. Москвич. Как и вы бывает на телеэкранах как эксперт по космосу.
За что часто получает неприятные и откровенно злобные комментарии от тех кто его видел на экране...

Его ЖЖ
Он в 70х учился в в МВТУ имени Баумана и тогда же загорелся термоядерным звездолётом. Он как и я фанатик межзвездных переселений. Но он однолюб. Любит термоядерную ракету на инерционном синтезе на бороводороде (то есть чистый синтез! не просто журавль в небе, "жар-птица"!!!) и не изменяет этой любви всю жизнь! Как влюбился студентом, так и ...
Тогда же, в конце 70х решал похожую задачу оптимизации межзвездной ракеты. Но он чётко фиксировал скорость истечения (брал какие получались из прикидок двигателя) и оценочный секундный расход топлива (это по сути всё связанные параметры с тягой или энерговооружённостью), но искал при этом оптимальную траекторию. То есть соотношение участков разгона-торможения и полёта по инерции. И тоже решал уже эту задачу не аналитически, а численными методами (притом даже без калькулятора!!! Калькулятор в 1978-м стоил 300 рублей! Почти 3 зарплаты МНС-а, а студенту ... даже при стипендии 55 р (+15 рублей от министерства обороны) - и не снилось)
Вот его выкладки:
То есть, можно сказать так (используя выше введенные термины). Он задавал L - дистанцию перелёта, u-скорость истечения из двигателя, сухую массу ракеты m и m-c-точкой, секундный расход топлива [кг/с] (два последних параметра по-сути можно было заменить одним - удельной тягой или удельной мощностью, на выбор), и он искал оптимальную R (массовое число, число Циолковского) и форму траектории долю инерционного участка во всей дистанции, обозначим (1-x). То есть доли активного (разгон-торможение) и инерциального участка x.
То есть, если мы искали оптимум ВЕРТИКАЛЬНО то, Иван в своё время искал оптимум ГОРИЗОНТАЛЬНО. И его заинтересовали мои кривые, сильно похожие на его.

В итоге я понял что мы ищем каждый свой локальные оптимумы, рассекая одну и ту же плоскость оптимизации, он поперёк, а я вдоль (по самому краю) и не видим глобального оптимума - на плоскости.
Ввести в уже найденное мной решение для ракеты с постоянно включенным двигателем поправку x на форму траектории было плёвым делом:
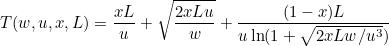 (17)
(17)
Еще раз. x - доля в дистанции L активного участка (разгона и торможения). 0<x<=1. То есть при x=1 формула вырождается в ту самую исходную (16):
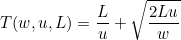
Последнее слагаемое - это время полёта по активному участку. То есть пассивный участок полёта (1-x)L делённая на пиковую скорость v. И из знаменателя ясно что пол логарифмом там - r - число Циолковского для торможения. И R для всей ракеты (разгон-торможение), R=r2. Это -о чевидно.
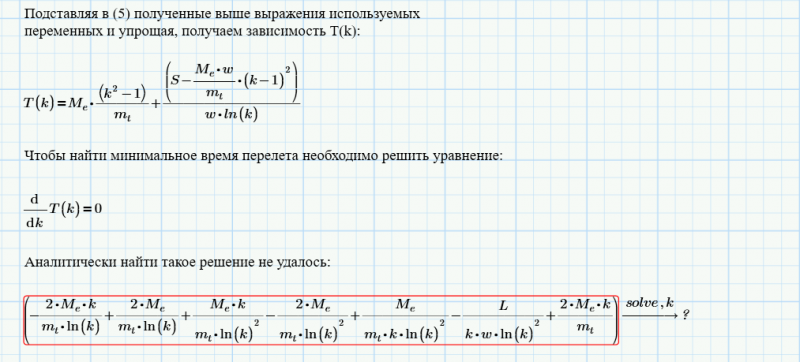
Взяв производные от выражения (17), одну по u, другую по x, и приравняв их к 0, получаем систему уравнений, которая по-идее дает аналитическое решение глобального оптимума:
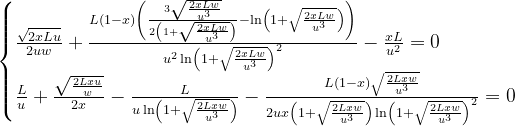
Красиво? Не правда ли?

И тут аналитика, думаю... бессильна.
Поэтому и я берусь за численные методы как когда-то это сделал Иван, в конец 70х даже не имея калькулятора под рукой (дорого!).

За что часто получает неприятные и откровенно злобные комментарии от тех кто его видел на экране...

Его ЖЖ
Он в 70х учился в в МВТУ имени Баумана и тогда же загорелся термоядерным звездолётом. Он как и я фанатик межзвездных переселений. Но он однолюб. Любит термоядерную ракету на инерционном синтезе на бороводороде (то есть чистый синтез! не просто журавль в небе, "жар-птица"!!!) и не изменяет этой любви всю жизнь! Как влюбился студентом, так и ...
Тогда же, в конце 70х решал похожую задачу оптимизации межзвездной ракеты. Но он чётко фиксировал скорость истечения (брал какие получались из прикидок двигателя) и оценочный секундный расход топлива (это по сути всё связанные параметры с тягой или энерговооружённостью), но искал при этом оптимальную траекторию. То есть соотношение участков разгона-торможения и полёта по инерции. И тоже решал уже эту задачу не аналитически, а численными методами (притом даже без калькулятора!!! Калькулятор в 1978-м стоил 300 рублей! Почти 3 зарплаты МНС-а, а студенту ... даже при стипендии 55 р (+15 рублей от министерства обороны) - и не снилось)
Вот его выкладки:
Алгоритм-АФ
Определение зависимостей между характеристиками межзвездного космического аппарата, требуемым временем и оптимальной траекторией перелета.
(Рассматриваемый алгоритм подходит для расчета полеты ракеты на любую дистанцию - хоть во двор к соседу, хоть к Альфе Центавра. Для определенности здесь и далее принимается перелет к Альфе Центавра. Алгоритм описывает для целей дискуссии в теме "Двигатель для межзвёздных перелётов" на Астрофоруме:
Двигатель для межзвёздных перелётов - Вселенная, жизнь, разум - Астрофорум – астрономический портал )
Рассматривается траектория с торможением у звезды-цели. В этом случае межзвездный полет состоит из трех участков - участка разгона до максимальной скорости, участка пассивного полета (аппарат движется по инерции), и участка торможения - участка, на котором приобретенная скорость "гасится".
Расчетная схема:
Рассчитываются параметры перелета с помощью простейшей одноступенчатой ракеты:
Исходными данными для расчета межзвездного перелета являются:
Me - конечная масса, масса двигателя + масса конструкции + масса ПН;
K - коэффициент конструктивного совершенства, отношение стартовой массы к конечной;
w - эффективная скорость истечения;
mt - скорость расхода массы топлива (рабочего тела);
S - дистанция межзвездного перелета.
Для расчетов используются уравнения ракетодинамики:
Уравнение (1) составлено в предположении равномерного расхода топлива на всем протяжении полета.
Уравнение (2) является уравнением Мещерского для случая полета в абсолютно свободном пространстве.
Уравнения (3,4) являются интегралами уравнения Мещерского.
Следовательно, определять минимальное время придется численно, для конкретных параметров перелета.
Контрольная точка.
Расчет выполненный ранее определил следующие параметры межзвездного перелета.
Результаты:
Результаты относятся к простейшему варианту ракеты.
Известные конструкторские приемы ракетостроения могут существенно снизить требуемое время межзвездного перелета.
То есть, можно сказать так (используя выше введенные термины). Он задавал L - дистанцию перелёта, u-скорость истечения из двигателя, сухую массу ракеты m и m-c-точкой, секундный расход топлива [кг/с] (два последних параметра по-сути можно было заменить одним - удельной тягой или удельной мощностью, на выбор), и он искал оптимальную R (массовое число, число Циолковского) и форму траектории долю инерционного участка во всей дистанции, обозначим (1-x). То есть доли активного (разгон-торможение) и инерциального участка x.
То есть, если мы искали оптимум ВЕРТИКАЛЬНО то, Иван в своё время искал оптимум ГОРИЗОНТАЛЬНО. И его заинтересовали мои кривые, сильно похожие на его.

В итоге я понял что мы ищем каждый свой локальные оптимумы, рассекая одну и ту же плоскость оптимизации, он поперёк, а я вдоль (по самому краю) и не видим глобального оптимума - на плоскости.
Ввести в уже найденное мной решение для ракеты с постоянно включенным двигателем поправку x на форму траектории было плёвым делом:
Еще раз. x - доля в дистанции L активного участка (разгона и торможения). 0<x<=1. То есть при x=1 формула вырождается в ту самую исходную (16):
Последнее слагаемое - это время полёта по активному участку. То есть пассивный участок полёта (1-x)L делённая на пиковую скорость v. И из знаменателя ясно что пол логарифмом там - r - число Циолковского для торможения. И R для всей ракеты (разгон-торможение), R=r2. Это -о чевидно.
Взяв производные от выражения (17), одну по u, другую по x, и приравняв их к 0, получаем систему уравнений, которая по-идее дает аналитическое решение глобального оптимума:
Красиво? Не правда ли?

И тут аналитика, думаю... бессильна.
Поэтому и я берусь за численные методы как когда-то это сделал Иван, в конец 70х даже не имея калькулятора под рукой (дорого!).



Это сообщение редактировалось 21.01.2023 в 17:07
A.s.> Мы тут не знаем начальную и конечную массу ракеты, не знаем числа Циолковского.
A.s.> То есть вы тут решили чуть другую задачу. Похожую. Но другую.
A.s.>
Вообще, правильнее исходить из того что мы имеем в реальности, а именно:
1) Расстояние на которое летим
2) конечную массу
3) и что-то про имеющуюся у нас энергетику.
И уже от этого танцевать и оптимизировать.
A.s.> То есть вы тут решили чуть другую задачу. Похожую. Но другую.
A.s.>

Вообще, правильнее исходить из того что мы имеем в реальности, а именно:
1) Расстояние на которое летим
2) конечную массу
3) и что-то про имеющуюся у нас энергетику.
И уже от этого танцевать и оптимизировать.

Дем> Вообще, правильнее исходить из того что мы имеем в реальности, а именно:
Дем> 1) Расстояние на которое летим
Дем> 2) конечную массу
Дем> 3) и что-то про имеющуюся у нас энергетику.
Дем> И уже от этого танцевать и оптимизировать.
От этого мы и пляшем. Расстояние - раз. Про энергетику которую имеем - два. Это и есть энерговооружённость. А варьируемый параметр - скорость истечения и по-сути скорость, до которой мы разгоняемся, пиковая (от него зависит форма траектории, тот самый параметр x). Тут есть явный экстремум. Минимум. Значит никто никогда пускать по ИНЫМ неоптимальным траекториям с неоптимальными параметрами u (слишком маленьким или слишком большим) и неоптимальным R такую ракету не будет.
Разумеется, если у вас есть ТЕХНИЧЕСКАЯ возможность варьировать скорость истечения в диапазоне оптимизации (потому что это не всегда получается).
Но для определённого типа звездолётов (условно "тысячелетников") как раз эта задача подходит идеально. Так ковчег Штерна в романе "Ковчег 47 Либра" как раз попадает под такую оптимизацию и на самом деле то что насчитал там Штерн - это неоптимальная конфигурация.
У него там вообще "детская ошибка" допущена. Но не будем будировать.
Ну а конечная масса, говорите?...
Разумеется надо знать. От нее и пляшут. Но она решается как отдельная задача (что мы собираемся делать у цели полёта?). В нашем расчете от нее никакого смысла. Наш расчёт изначально в смысле абсолютных значений масс - безразмерен. Мы при оптимизации ищем оптимальное число Циолковского R. Когда мы его знаем, умножаем ту конечную массу которую вы заказали нам (согласно заданию полёта) на наше R и получаем стартовую массу.
Вот и всё.
Но это, конечно только начало.
Не вечер. Мы еще не игрались со ступенями. Там совсем начинается цирк и гонки по вертикали...
Я долго был уверен, что если у вас нет избыточной энерговооруженности (как у ЖРД в своём классе, и у бомболёта в своём), то бессмысленно играть со ступенями. Для того же ионника, например. Но мне давеча показали "елку"-палку на 8 ступеней и с общим массовым числом R=1000, которая, как не странно обещает добраться до А.Центавры на 100 лет быстрей, чем самая оптимальная одноступенчатая ракета у меня с подобной же энерговооруженностью. Мы брали пока фантастическую (но вполне мыслимую) ~2 кВт/кг. Конечно в отличии от нашей оптимальной, от этой "ёлки" прилетит к цели с гулькин нос. Чудо оплачивается теряемой по дороге массой. Ничто не дается нашару. Но в сущности, все знают что вопрос не детский и порой надо хорошо платить. 1000 - массовое число? Для некоторых задач (автомат-разведчик) это вполне приемлемый размен. Главное что на самом деле многоступенчатый ионник, как не странно, может иметь смысл! Это - благая весть. Там еще возникает ряд плюсов (например нет у реакторов срока работы в несколько сотен лет!)
В общем, хотя о звездолётах вспоминают нынче часто (в связи с экзопланетами), но всегда одно и то же, сдирая друг у друга одни и те же заскорузлые банальности. Скучно-однообразно. А на самом деле там есть масса интересного и даже толком нехоженного. Оказывается. Только копни!

Дем> 1) Расстояние на которое летим
Дем> 2) конечную массу
Дем> 3) и что-то про имеющуюся у нас энергетику.
Дем> И уже от этого танцевать и оптимизировать.
От этого мы и пляшем. Расстояние - раз. Про энергетику которую имеем - два. Это и есть энерговооружённость. А варьируемый параметр - скорость истечения и по-сути скорость, до которой мы разгоняемся, пиковая (от него зависит форма траектории, тот самый параметр x). Тут есть явный экстремум. Минимум. Значит никто никогда пускать по ИНЫМ неоптимальным траекториям с неоптимальными параметрами u (слишком маленьким или слишком большим) и неоптимальным R такую ракету не будет.
Разумеется, если у вас есть ТЕХНИЧЕСКАЯ возможность варьировать скорость истечения в диапазоне оптимизации (потому что это не всегда получается).
Но для определённого типа звездолётов (условно "тысячелетников") как раз эта задача подходит идеально. Так ковчег Штерна в романе "Ковчег 47 Либра" как раз попадает под такую оптимизацию и на самом деле то что насчитал там Штерн - это неоптимальная конфигурация.
У него там вообще "детская ошибка" допущена. Но не будем будировать.
Ну а конечная масса, говорите?...
Разумеется надо знать. От нее и пляшут. Но она решается как отдельная задача (что мы собираемся делать у цели полёта?). В нашем расчете от нее никакого смысла. Наш расчёт изначально в смысле абсолютных значений масс - безразмерен. Мы при оптимизации ищем оптимальное число Циолковского R. Когда мы его знаем, умножаем ту конечную массу которую вы заказали нам (согласно заданию полёта) на наше R и получаем стартовую массу.
Вот и всё.
Но это, конечно только начало.
Не вечер. Мы еще не игрались со ступенями. Там совсем начинается цирк и гонки по вертикали...
Я долго был уверен, что если у вас нет избыточной энерговооруженности (как у ЖРД в своём классе, и у бомболёта в своём), то бессмысленно играть со ступенями. Для того же ионника, например. Но мне давеча показали "елку"-палку на 8 ступеней и с общим массовым числом R=1000, которая, как не странно обещает добраться до А.Центавры на 100 лет быстрей, чем самая оптимальная одноступенчатая ракета у меня с подобной же энерговооруженностью. Мы брали пока фантастическую (но вполне мыслимую) ~2 кВт/кг. Конечно в отличии от нашей оптимальной, от этой "ёлки" прилетит к цели с гулькин нос. Чудо оплачивается теряемой по дороге массой. Ничто не дается нашару. Но в сущности, все знают что вопрос не детский и порой надо хорошо платить. 1000 - массовое число? Для некоторых задач (автомат-разведчик) это вполне приемлемый размен. Главное что на самом деле многоступенчатый ионник, как не странно, может иметь смысл! Это - благая весть. Там еще возникает ряд плюсов (например нет у реакторов срока работы в несколько сотен лет!)
В общем, хотя о звездолётах вспоминают нынче часто (в связи с экзопланетами), но всегда одно и то же, сдирая друг у друга одни и те же заскорузлые банальности. Скучно-однообразно. А на самом деле там есть масса интересного и даже толком нехоженного. Оказывается. Только копни!



Это сообщение редактировалось 22.01.2023 в 04:14
A.s.> Ищу знакомые буквы.  Я и раньше смотрел. И сейчас и раньше я вижу что вы решаете (вроде верно решаете) другую (чуть) задачу. Похожую но другую.
Я и раньше смотрел. И сейчас и раньше я вижу что вы решаете (вроде верно решаете) другую (чуть) задачу. Похожую но другую.
Алекс. Если честно Вы порой так странно мыслите.. Лично я решал задачу как математик и частично ракетчик. То есть брал переменные которые можно задать для задачи и вычислял те, что вычислить куда сложнее. Это оказался пройденный путь. Для которого пришлось брать очень сложные интегралы от логарифма. Они не входят в обычный курс мат анализа и если бы я пробовал решить задачу в конце 90х, то скорей всего не решил бы.
Но результат я получил. И очень необычный результат. Прямо скажу, эту формулу я вывел уже два раза (в 2019 и 2020) но она настолько странная, что я опять думаю, что где-то накосячил и хочу оформить эту работу правильно, чтобы можно было проверить.
Вот она
L= u*T * (M0,5-m0,5)/(M0,5+m0,5)
Ну или
L= u*T * (Z0,5-1)/(Z0,5+1)
Где L= весь пройденный путь (он точки старта, до точки завершения торможения)
u- удельный импульс
T- время перелета
M- начальная масса, m-конечная (сухая) масса, Z- число Циолковского
Ван нужно вытащить другие соотношения? Да нет ничего легче!
Вот зависимость Т от Z
T= (Z0,5+1)/(Z0,5-1)*L/u
Могу и Т от Z вывести
Но главное здесь не это
Видите эту громозкую часть формулы?
(M0,5-m0,5)/(M0,5+m0,5)
С учетом того, что в межзвездных перелетах M >> m она будет очень близка к 1.А значит для таких перелетов можно оценивать:
L=u*T
То есть максимально возможная дальность перелета (при непрерывной работе двигателей!) зависит только от удельного импульса и времени перелета. Зная удельный импульс и дистанцию можно подобрать и время.
Скажем если мы хотим пролететь 1 световой год за 100 лет, то для этого нужен удельный импульс хотя бы в 100 раз меньше скорости света. Будет он больше - хорошо. Меньше- пролететь за сто лет не выйдет.
Второй вывод - эта схема перелета самая не оптимальная из возможных, что может быть для межзвездного корабля. Мы слишком большую часть трассы проходим с небольшой скоростью. А пиковую скорость (набранную таким трудом) слишком быстро гасим при торможении.
Вывод: межзвездный перелет нужно осуществлять так, чтобы большая часть перелета шла по инерции. Участки разгона и торможения должны быть очень небольшими. Здесь надо считать, но скорей всего пренебрежительно малыми относительно всего времени перелета. Но в реальной конструкции все будет определятся технически возможными решениями.
P.S Но все таки формулу я пересчитаю.
 Я и раньше смотрел. И сейчас и раньше я вижу что вы решаете (вроде верно решаете) другую (чуть) задачу. Похожую но другую.
Я и раньше смотрел. И сейчас и раньше я вижу что вы решаете (вроде верно решаете) другую (чуть) задачу. Похожую но другую.Алекс. Если честно Вы порой так странно мыслите.. Лично я решал задачу как математик и частично ракетчик. То есть брал переменные которые можно задать для задачи и вычислял те, что вычислить куда сложнее. Это оказался пройденный путь. Для которого пришлось брать очень сложные интегралы от логарифма. Они не входят в обычный курс мат анализа и если бы я пробовал решить задачу в конце 90х, то скорей всего не решил бы.
Но результат я получил. И очень необычный результат. Прямо скажу, эту формулу я вывел уже два раза (в 2019 и 2020) но она настолько странная, что я опять думаю, что где-то накосячил и хочу оформить эту работу правильно, чтобы можно было проверить.
Вот она
L= u*T * (M0,5-m0,5)/(M0,5+m0,5)
Ну или
L= u*T * (Z0,5-1)/(Z0,5+1)
Где L= весь пройденный путь (он точки старта, до точки завершения торможения)
u- удельный импульс
T- время перелета
M- начальная масса, m-конечная (сухая) масса, Z- число Циолковского
Ван нужно вытащить другие соотношения? Да нет ничего легче!
Вот зависимость Т от Z
T= (Z0,5+1)/(Z0,5-1)*L/u
Могу и Т от Z вывести
Но главное здесь не это
Видите эту громозкую часть формулы?
(M0,5-m0,5)/(M0,5+m0,5)
С учетом того, что в межзвездных перелетах M >> m она будет очень близка к 1.А значит для таких перелетов можно оценивать:
L=u*T
То есть максимально возможная дальность перелета (при непрерывной работе двигателей!) зависит только от удельного импульса и времени перелета. Зная удельный импульс и дистанцию можно подобрать и время.
Скажем если мы хотим пролететь 1 световой год за 100 лет, то для этого нужен удельный импульс хотя бы в 100 раз меньше скорости света. Будет он больше - хорошо. Меньше- пролететь за сто лет не выйдет.
Второй вывод - эта схема перелета самая не оптимальная из возможных, что может быть для межзвездного корабля. Мы слишком большую часть трассы проходим с небольшой скоростью. А пиковую скорость (набранную таким трудом) слишком быстро гасим при торможении.
Вывод: межзвездный перелет нужно осуществлять так, чтобы большая часть перелета шла по инерции. Участки разгона и торможения должны быть очень небольшими. Здесь надо считать, но скорей всего пренебрежительно малыми относительно всего времени перелета. Но в реальной конструкции все будет определятся технически возможными решениями.
P.S Но все таки формулу я пересчитаю.


PSS> Для которого пришлось брать очень сложные интегралы от логарифма. Они не входят в обычный курс мат анализа и если бы я пробовал решить задачу в конце 90х, то скорей всего не решил бы.
А какие проблемы? В ряд - и вперёд.
PSS> Второй вывод - эта схема перелета самая не оптимальная из возможных, что может быть для межзвездного корабля. Мы слишком большую часть трассы проходим с небольшой скоростью. А пиковую скорость (набранную таким трудом) слишком быстро гасим при торможении.
А другие невозможны. "Сэр, но как?"
Мы даже приблизительно не можем пока представить себе способа придать массивному плотному и твёрдому физическому телу пинком не то что 0,5С - хотя бы жалкую 0,01с.
PSS> Вывод: межзвездный перелет нужно осуществлять так, чтобы большая часть перелета шла по инерции. Участки разгона и торможения должны быть очень небольшими. Здесь надо считать, но скорей всего пренебрежительно малыми относительно всего времени перелета.
Совершенно тривиальный результат.
Достойный анекдота про Холмса, Ватсона и математика
Вызванный в сущности недоучётом еще одного граничного условия - ограничений сверху по тяге/мощности.
Осмысленной может быть задача о варьировании УИ и нахождении оптимального закона.
А какие проблемы? В ряд - и вперёд.
PSS> Второй вывод - эта схема перелета самая не оптимальная из возможных, что может быть для межзвездного корабля. Мы слишком большую часть трассы проходим с небольшой скоростью. А пиковую скорость (набранную таким трудом) слишком быстро гасим при торможении.
А другие невозможны. "Сэр, но как?"
Мы даже приблизительно не можем пока представить себе способа придать массивному плотному и твёрдому физическому телу пинком не то что 0,5С - хотя бы жалкую 0,01с.
PSS> Вывод: межзвездный перелет нужно осуществлять так, чтобы большая часть перелета шла по инерции. Участки разгона и торможения должны быть очень небольшими. Здесь надо считать, но скорей всего пренебрежительно малыми относительно всего времени перелета.
Совершенно тривиальный результат.
Достойный анекдота про Холмса, Ватсона и математика

Вызванный в сущности недоучётом еще одного граничного условия - ограничений сверху по тяге/мощности.
Осмысленной может быть задача о варьировании УИ и нахождении оптимального закона.


PSS>> Второй вывод - эта схема перелета самая не оптимальная из возможных, что может быть для межзвездного корабля. Мы слишком большую часть трассы проходим с небольшой скоростью. А пиковую скорость (набранную таким трудом) слишком быстро гасим при торможении.
Fakir> А другие невозможны. "Сэр, но как?"
Вовсе нет,возможны. Но здесь решал задачу перелета с постоянной тягой все время перелета.
По сути,эта задача обратная той что любят приводить (в первую очередь для межзвездных перелетов). Мгновенный разгон до нужной скорости и полет дальше по инерции,потом столь мгновенное торможение
Этот режим может быть для любого аппарата,в том числе и существующего. Вопрос сколько он пролетит.
Собственно потом можно и провести оценку для разного импульса. Но пока точно разберусь с этой задачей.
Fakir> А другие невозможны. "Сэр, но как?"
Вовсе нет,возможны. Но здесь решал задачу перелета с постоянной тягой все время перелета.
По сути,эта задача обратная той что любят приводить (в первую очередь для межзвездных перелетов). Мгновенный разгон до нужной скорости и полет дальше по инерции,потом столь мгновенное торможение
Этот режим может быть для любого аппарата,в том числе и существующего. Вопрос сколько он пролетит.
Собственно потом можно и провести оценку для разного импульса. Но пока точно разберусь с этой задачей.


PSS> Вовсе нет,возможны.
?!
PSS> Мгновенный разгон до нужной скорости
"Не бывает".
Не бывает мгновенного разгона массивных тел, тем более до релятивистских скоростей.
И даже маломассивных, но с ненулевой массой покоя. Даже в ускорителе разгон не мгновенный. Каким-то приближением еще может быть бета-распад в отдельных случаях.
?!
PSS> Мгновенный разгон до нужной скорости
"Не бывает".
Не бывает мгновенного разгона массивных тел, тем более до релятивистских скоростей.
И даже маломассивных, но с ненулевой массой покоя. Даже в ускорителе разгон не мгновенный. Каким-то приближением еще может быть бета-распад в отдельных случаях.


PSS>> Вовсе нет,возможны.
Fakir> ?!
Самый очевидный вариант - многоступенчатая система. Когда разгоняют корабль и тормозят разные ступени.
Собственно я также думал, почему я не видел оценок накопительной системы, только прямоточника. Когда топливо большей частью только на разгон, а на торможение собирается во время перелета. Причем и во время сбора он должен заметно затормозиться.
Ну и солнечный парус. У которого удельный импульс вообще бесконечный, так как нет потерь массы. Но тяга очень и очень быстро падает с удалением от звезды.
Во всех этих случаях динамика разгона/торможения будет кардинально отличаться от изначально разобранного случая.
PSS>> Мгновенный разгон до нужной скорости
Fakir> "Не бывает".
Конечно не бывает. Но для нулевого приближения часто используют. Впрочем, по сути там часто подразумевается, что участок разгона/торможения просто куда меньше общей дистанции перелета.
Fakir> ?!
Самый очевидный вариант - многоступенчатая система. Когда разгоняют корабль и тормозят разные ступени.
Собственно я также думал, почему я не видел оценок накопительной системы, только прямоточника. Когда топливо большей частью только на разгон, а на торможение собирается во время перелета. Причем и во время сбора он должен заметно затормозиться.
Ну и солнечный парус. У которого удельный импульс вообще бесконечный, так как нет потерь массы. Но тяга очень и очень быстро падает с удалением от звезды.
Во всех этих случаях динамика разгона/торможения будет кардинально отличаться от изначально разобранного случая.
PSS>> Мгновенный разгон до нужной скорости
Fakir> "Не бывает".
Конечно не бывает. Но для нулевого приближения часто используют. Впрочем, по сути там часто подразумевается, что участок разгона/торможения просто куда меньше общей дистанции перелета.


PSS> Самый очевидный вариант - многоступенчатая система.
Да сколько угодно. Хоть 100-ступенчатая. Мгновенным это ускорение не сделает.
PSS> Ну и солнечный парус.
"Это другое". Вообще другой класс, и задача в рассматриваемой исходно постановке вообще не имеет смысла - её и ставить по-другому надо.
Для неё мгновенное ускорение вдвойне невозможно.
Кстати, с лазерным парусом вообще много проблем, о которых обычно не думают (не понимают самого их существования), и если заняться по-хорошему - то оптимизация с кучей неочевидных нюансов (вплоть до "двумерной" траектории).
Другое дело, что это всё следует отнести по разряду игр ума и "суемыслия", говоря церковным языком.
PSS> Собственно я также думал, почему я не видел оценок накопительной системы, только прямоточника. Когда топливо большей частью только на разгон, а на торможение собирается во время перелета. Причем и во время сбора он должен заметно затормозиться.
Там вообще дюжина бочек арестантов. С прямоточниками проблем овердофига, концептуальных; эти проблемы как правило полностью игнорируются, вот концептуально - слепое пятно. Практически все предлагаемые концепты способны по сути работать только на торможение, разными способами. И то не очень эффективно.
Сама способность прямоточника сработать на ускорение крайне неочевидна и никем не доказана. Может быть, и есть там лазейки, но про это вообще никто не думал даже, т.к. самой проблемы не видят.
PSS> Конечно не бывает. Но для нулевого приближения часто используют.
Бессмысленно и некорректно в корне. Ну если только перелёт не на 100 св.лет. Что рассматривать тоже бессмысленно
Сколько-нибудь осмысленным может быть рассмотрение ну пусть до 10 св. лет. Всё, что дальше - суемыслие при нынешнем не то что техническом уровне, а на уровне сегодняшних знаний.
Да сколько угодно. Хоть 100-ступенчатая. Мгновенным это ускорение не сделает.
PSS> Ну и солнечный парус.
"Это другое". Вообще другой класс, и задача в рассматриваемой исходно постановке вообще не имеет смысла - её и ставить по-другому надо.
Для неё мгновенное ускорение вдвойне невозможно.
Кстати, с лазерным парусом вообще много проблем, о которых обычно не думают (не понимают самого их существования), и если заняться по-хорошему - то оптимизация с кучей неочевидных нюансов (вплоть до "двумерной" траектории).
Другое дело, что это всё следует отнести по разряду игр ума и "суемыслия", говоря церковным языком.
PSS> Собственно я также думал, почему я не видел оценок накопительной системы, только прямоточника. Когда топливо большей частью только на разгон, а на торможение собирается во время перелета. Причем и во время сбора он должен заметно затормозиться.
Там вообще дюжина бочек арестантов. С прямоточниками проблем овердофига, концептуальных; эти проблемы как правило полностью игнорируются, вот концептуально - слепое пятно. Практически все предлагаемые концепты способны по сути работать только на торможение, разными способами. И то не очень эффективно.
Сама способность прямоточника сработать на ускорение крайне неочевидна и никем не доказана. Может быть, и есть там лазейки, но про это вообще никто не думал даже, т.к. самой проблемы не видят.
PSS> Конечно не бывает. Но для нулевого приближения часто используют.
Бессмысленно и некорректно в корне. Ну если только перелёт не на 100 св.лет. Что рассматривать тоже бессмысленно

Сколько-нибудь осмысленным может быть рассмотрение ну пусть до 10 св. лет. Всё, что дальше - суемыслие при нынешнем не то что техническом уровне, а на уровне сегодняшних знаний.


PSS>> Самый очевидный вариант - многоступенчатая система.
Fakir> Да сколько угодно. Хоть 100-ступенчатая. Мгновенным это ускорение не сделает.
А никто не требовал мгновенное ускорение. И не говорил, что возможно. Факир, лучше почитайте всю ветку. Здесь обсуждалась конкретная задача, не надо выхватывать только косвенные второстепенные детали.
Fakir> "Это другое". Вообще другой класс, и задача в рассматриваемой исходно постановке вообще не имеет смысла - её и ставить по-другому надо.
Конечно, другое. О чем я прямо написал в посте выше.
Fakir> Для неё мгновенное ускорение вдвойне невозможно.
А кто-то требовал мгновенное ускорение?
Fakir> Сама способность прямоточника сработать на ускорение крайне не очевидна и никем не доказана. Может быть, и есть там лазейки, но про это вообще никто не думал даже, т.к. самой проблемы не видят.
Правда я выше требовал разгонятся на заранее запасенном топливе, топливо межзвездного газа для торможения накопить по дороге. Зачем только Факир стал доказывать, что не показал возможность разгона для систем с захватом?
Fakir> Сколько-нибудь осмысленным может быть рассмотрение ну пусть до 10 св. лет. Всё, что дальше - суемыслие при нынешнем не то что техническом уровне, а на уровне сегодняшних знаний.
Обычно здесь обсуждали перелет на 4.5 св года. По понятным причинам. Проблема в том, что уже по современным знаниям в диапазоне 4-10 световых лет очень и очень мало звезд. И интересных там, можно считать, нет. После того как развенчали существование планетной системы и звезды Барнарда. Так что сейчас ближайшая самая интересная звезда - Тау Кита. 12 световых лет.
Fakir> Да сколько угодно. Хоть 100-ступенчатая. Мгновенным это ускорение не сделает.
А никто не требовал мгновенное ускорение. И не говорил, что возможно. Факир, лучше почитайте всю ветку. Здесь обсуждалась конкретная задача, не надо выхватывать только косвенные второстепенные детали.
Fakir> "Это другое". Вообще другой класс, и задача в рассматриваемой исходно постановке вообще не имеет смысла - её и ставить по-другому надо.
Конечно, другое. О чем я прямо написал в посте выше.
Fakir> Для неё мгновенное ускорение вдвойне невозможно.
А кто-то требовал мгновенное ускорение?
Fakir> Сама способность прямоточника сработать на ускорение крайне не очевидна и никем не доказана. Может быть, и есть там лазейки, но про это вообще никто не думал даже, т.к. самой проблемы не видят.
Правда я выше требовал разгонятся на заранее запасенном топливе, топливо межзвездного газа для торможения накопить по дороге. Зачем только Факир стал доказывать, что не показал возможность разгона для систем с захватом?
Fakir> Сколько-нибудь осмысленным может быть рассмотрение ну пусть до 10 св. лет. Всё, что дальше - суемыслие при нынешнем не то что техническом уровне, а на уровне сегодняшних знаний.
Обычно здесь обсуждали перелет на 4.5 св года. По понятным причинам. Проблема в том, что уже по современным знаниям в диапазоне 4-10 световых лет очень и очень мало звезд. И интересных там, можно считать, нет. После того как развенчали существование планетной системы и звезды Барнарда. Так что сейчас ближайшая самая интересная звезда - Тау Кита. 12 световых лет.


Copyright © Balancer 1997..2024
Создано 03.12.2016
Связь с владельцами и администрацией сайта: anonisimov@gmail.com, rwasp1957@yandex.ru и admin@balancer.ru.
Создано 03.12.2016
Связь с владельцами и администрацией сайта: anonisimov@gmail.com, rwasp1957@yandex.ru и admin@balancer.ru.
 Fakir
Fakir

 инфо
инфо инструменты
инструменты Полл
Полл

 Alex_semenov
Alex_semenov




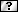 Alex_semenov
Alex_semenov











 Fakir
Fakir
