-
/6561348.png)
Идиот-клуб [8]
Теги:
loderunner> Вам уже несколько раз объяснили, что вакуум - не пустой, что Эйнштейн не говорил, что вакуум пустой, что т.н. эйнштейновск... бла, бла, бла...
Халва, халва, халва...
Чего толку-то одно и то же невпопад трундеть?
Как это эйнштейн не говорил, а это что?
Свет по СТО где распространяется? Что говорил САМ основатель секты - в пустом пространстве без материи или в материальной среде?
Халва, халва, халва...
Чего толку-то одно и то же невпопад трундеть?
Как это эйнштейн не говорил, а это что?
...Ибо существуют две объективных реальности — пространство-время (что являет собой континуум)иматерия
Свет по СТО где распространяется? Что говорил САМ основатель секты - в пустом пространстве без материи или в материальной среде?


V.a.C.> Так вы разберитесь в двух-то соснах - или
Эйнштейново пространство-время может нести энергию и информации, т.е. является материальным объектом.
V.a.C.> А если оно не пустое, т.е.является материальной средой для их распространения с постоянной для данной среды скоростью С, то где тогда нахрен оказывается принцип относительности ИСО, если эта самая среда (эфир, физический вакуум и т.д.) как раз и является той самой нулевой (привилегированной) ИСО от которой и шарахаются, как черт от святого причастия, члены секты релятивистов?
Как ни странно, с этой средой не может быть связана никакая ИСО, т.к. свои функции - нести сигналы со световой скоростью - оно одинаково хорошо выполняет в любой ИСО.
Т.е. материальный объект есть, таким свойством, как скорость он не обладает.
Эйнштейново пространство-время может нести энергию и информации, т.е. является материальным объектом.
V.a.C.> А если оно не пустое, т.е.является материальной средой для их распространения с постоянной для данной среды скоростью С, то где тогда нахрен оказывается принцип относительности ИСО, если эта самая среда (эфир, физический вакуум и т.д.) как раз и является той самой нулевой (привилегированной) ИСО от которой и шарахаются, как черт от святого причастия, члены секты релятивистов?

Как ни странно, с этой средой не может быть связана никакая ИСО, т.к. свои функции - нести сигналы со световой скоростью - оно одинаково хорошо выполняет в любой ИСО.
Т.е. материальный объект есть, таким свойством, как скорость он не обладает.


V.a.C.>> Так вы разберитесь в двух-то соснах - или
Сергей-4030> Солнце ненаглядное, ты знаешь, что такое термины и зачем они нужны? Ты типа почитай что-нибудь при случае. А то твои терминологические изыски уже прискучили. То, что те дебил - в общем, не страшно, иного не дано, ты же опроверганец. А вот то, что не понимаешь, что тебе говорят - это как-то неудобно. Несмешно.
Чо, Серый, заглянул поржать над "опроверганцем", а тут оказывается
Ну это кому как - наши-то просто колобками катаются
Ты лучше за этим к глистунгу aka галахический поц - нынче на хозяйстве он за клоуна - уж не откажет же подельничку, засасывающему две подряд, но исключающему третью
Сергей-4030> Солнце ненаглядное, ты знаешь, что такое термины и зачем они нужны? Ты типа почитай что-нибудь при случае. А то твои терминологические изыски уже прискучили. То, что те дебил - в общем, не страшно, иного не дано, ты же опроверганец. А вот то, что не понимаешь, что тебе говорят - это как-то неудобно. Несмешно.
Чо, Серый, заглянул поржать над "опроверганцем", а тут оказывается
Несмешно.
Ну это кому как - наши-то просто колобками катаются

Ты лучше за этим к глистунгу aka галахический поц - нынче на хозяйстве он за клоуна - уж не откажет же подельничку, засасывающему две подряд, но исключающему третью



V.a.C.>> Так вы разберитесь в двух-то соснах - или
Yuriy> Эйнштейново пространство-время может нести энергию и информации, т.е. является материальным объектом.
Эйнштейново пространство-время является математической моделью, которая по (принципиально) неизвестным нам причинам хорошо описывает поведение реальных вещей. Точно так же и поле - поле есть математическая абстракция, хорошо описывающая реальные вещи. Причина, по которой поле хорошо описывает поведение реальных вещей (скажем, притяжение/отталкивание заряженных частиц) нам неизвестна сейчас и, вполне вероятно, никогда не будет известно вовсе. Но это неважно.
Yuriy> Эйнштейново пространство-время может нести энергию и информации, т.е. является материальным объектом.
Эйнштейново пространство-время является математической моделью, которая по (принципиально) неизвестным нам причинам хорошо описывает поведение реальных вещей. Точно так же и поле - поле есть математическая абстракция, хорошо описывающая реальные вещи. Причина, по которой поле хорошо описывает поведение реальных вещей (скажем, притяжение/отталкивание заряженных частиц) нам неизвестна сейчас и, вполне вероятно, никогда не будет известно вовсе. Но это неважно.


V.a.C.> Ты лучше за этим к глистунгу aka галахический поц - нынче на хозяйстве он за клоуна - уж не откажет же подельничку, засасывающему две подряд, но исключающему третью 
Ты, опроверганец, того, не выеживайся. Практика показывает, что опроверганцев в этом форуме модерируют плотнее, чем нормальных.

Ты, опроверганец, того, не выеживайся. Практика показывает, что опроверганцев в этом форуме модерируют плотнее, чем нормальных.


Yuriy> Как ни странно, с этой средой не может быть связана никакая ИСО, т.к. свои функции - нести сигналы со световой скоростью - оно одинаково хорошо выполняет в любой ИСО.
Yuriy> Т.е. материальный объект есть, таким свойством, как скорость он не обладает.
Как ни странно?
Для того чтобы свести концы с концами при толковании результатов опыта - который, как выясняется, изначально не мог ни подтвердить, ни опровергнуть того, ради чего затевался - выдумывается некоторая несуществующая в реальности условность, типа тени от объекта, но без самого объекта, с ее помощью доказывается, что дважды два = пять - и мама не горюй - революция в естествознании, вершина человеческого познания - разгениальная ТО! И гений всех времен и народов - весь в белом!
Правда потом во все стороны начинают лезть гвозди и нитки от неряшливо сшитой "θеории", но это уже никого не е.б. - мусор под ковер сноровисто заметает выдрессированная когорта "профессиональных рэволюционэров" на ходу деловито затыкающих рты несогласным и засирая мозги несмышленым.
И так уже второе столетие - зашибись, наука, блинн!
Yuriy> Т.е. материальный объект есть, таким свойством, как скорость он не обладает.
Как ни странно?

Для того чтобы свести концы с концами при толковании результатов опыта - который, как выясняется, изначально не мог ни подтвердить, ни опровергнуть того, ради чего затевался - выдумывается некоторая несуществующая в реальности условность, типа тени от объекта, но без самого объекта, с ее помощью доказывается, что дважды два = пять - и мама не горюй - революция в естествознании, вершина человеческого познания - разгениальная ТО! И гений всех времен и народов - весь в белом!

Правда потом во все стороны начинают лезть гвозди и нитки от неряшливо сшитой "θеории", но это уже никого не е.б. - мусор под ковер сноровисто заметает выдрессированная когорта "профессиональных рэволюционэров" на ходу деловито затыкающих рты несогласным и засирая мозги несмышленым.
И так уже второе столетие - зашибись, наука, блинн!



Это сообщение редактировалось 19.01.2012 в 02:27
V.a.C.>> Ты лучше за этим к глистунгу aka галахический поц - нынче на хозяйстве он за клоуна - уж не откажет же подельничку, засасывающему две подряд, но исключающему третью 
Сергей-4030> Ты, опроверганец, того, не выеживайся. Практика показывает, что опроверганцев в этом форуме модерируют плотнее, чем нормальных.
И чо? Удавиться теперь што ли?
Меня вон на хоботе пытались раком поставить, чтобы я им пятки лизал
ага, разбежался, аж падаю!

Сергей-4030> Ты, опроверганец, того, не выеживайся. Практика показывает, что опроверганцев в этом форуме модерируют плотнее, чем нормальных.
И чо? Удавиться теперь што ли?
Меня вон на хоботе пытались раком поставить, чтобы я им пятки лизал
ага, разбежался, аж падаю!



V.a.C.> Правда потом во все стороны начинают лезть гвозди и нитки от неряшливо сшитой "θеории"
Пару примеров этих "гвоздей и ниток" и "неряшливости" можете привести?
Пару примеров этих "гвоздей и ниток" и "неряшливости" можете привести?


V.a.C.>> Правда потом во все стороны начинают лезть гвозди и нитки от неряшливо сшитой "θеории"
loderunner> Пару примеров этих "гвоздей и ниток" и "неряшливости" можете привести?
Могу - берешь несложное заданьице, на коем уже который подряд сектант истинной веры будто язык проглотил, т.е. вписываешь семейство кривых "классической" формулы ДЭ в граничные условия, что на левой картинке.
Если получится!
Или строишь по "классической" формуле семейство эксцентрических волновых изоповерхностей движущегося источника и, закончив нелегкий труд, тихо охереваешь.
loderunner> Пару примеров этих "гвоздей и ниток" и "неряшливости" можете привести?
Могу - берешь несложное заданьице, на коем уже который подряд сектант истинной веры будто язык проглотил, т.е. вписываешь семейство кривых "классической" формулы ДЭ в граничные условия, что на левой картинке.
Если получится!

Или строишь по "классической" формуле семейство эксцентрических волновых изоповерхностей движущегося источника и, закончив нелегкий труд, тихо охереваешь.


V.a.C.> Так вот и впиши семейство кривых "классической" формулы ДЭ в граничные условия, что на левой картинке, а мы дружно поржём - я + те кто врубается. 
Катя, ты правда не видишь, что твой Замятин/Акимов - идиот? Значит, ты сам такой:
Откуда угол θ - угол наблюдения? Мы ведь наблюдаем теми же, допустим, электромагнитными колебаниями, типа глазами. Афтар пишет, что фронт только что пришёл к нам, значит мы видим источник i в точке о, а, не в точке B. Вот и весь нехитрый трюк афтара - обозначить как θ совсем другую величину, чем в классике, а потом сравнивать, как будто бы это одно и то же. О чём, собственно, и написано в УФН. (Ну, и про сами расчёты через сложение векторов скромно промолчим: нет никакого физического смысла векторно складывать скорость звука (света) со скоростью источника.)
V.a.C.> Представишь формулу, как спрошено - ω=f(g), сразу расскажу и покажу, что для чего.
Полудрагоценный, тебе уже открытым текстом сказали - математическое описание движения обратного маятника ничем не отличается от описания движения "обычного" физического маятника. В Интернете полно такого материала. Хоть в Википедии. Почитай, вдруг сразу и отпустит. Врочем, подозреваю, потребителям акимовых и замятиных уже ничего не поможет.

Катя, ты правда не видишь, что твой Замятин/Акимов - идиот? Значит, ты сам такой:
Рис. 1. Чертеж (а) представляет собой застывшее изображение процесса распространения волн при движущемся источнике колебаний ( i ). Пока волновой фронт, испущенный из точки 0, дойдет до точки А, источник колебаний i окажется в точке В. Чтобы найти выражения для векторной суммы векторов v и c, на чертеже (б) показан вспомогательный прямоугольный треугольник.
...............(4)
Формула (4) есть истинное, абсолютно точное выражение, описывающее эффект Доплера для любых значений параметра β.(5)
С точки зрения математики выражения (4) и (5) отражают один и тот же математический факт, однако с точки зрения физики было бы ошибкой считать φ углом наблюдения; им является угол θ
Откуда угол θ - угол наблюдения? Мы ведь наблюдаем теми же, допустим, электромагнитными колебаниями, типа глазами. Афтар пишет, что фронт только что пришёл к нам, значит мы видим источник i в точке о, а, не в точке B. Вот и весь нехитрый трюк афтара - обозначить как θ совсем другую величину, чем в классике, а потом сравнивать, как будто бы это одно и то же. О чём, собственно, и написано в УФН. (Ну, и про сами расчёты через сложение векторов скромно промолчим: нет никакого физического смысла векторно складывать скорость звука (света) со скоростью источника.)
V.a.C.> Представишь формулу, как спрошено - ω=f(g), сразу расскажу и покажу, что для чего.
Полудрагоценный, тебе уже открытым текстом сказали - математическое описание движения обратного маятника ничем не отличается от описания движения "обычного" физического маятника. В Интернете полно такого материала. Хоть в Википедии. Почитай, вдруг сразу и отпустит. Врочем, подозреваю, потребителям акимовых и замятиных уже ничего не поможет.



Это сообщение редактировалось 19.01.2012 в 11:14
V.a.C.>> Представишь формулу, как спрошено - ω=f(g), сразу расскажу и покажу, что для чего.
ER*> Полудрагоценный, тебе уже открытым текстом сказали - математическое описание движения обратного маятника ничем не отличается от описания движения "обычного" физического маятника. В Интернете полно такого материала. Хоть в Википедии. Почитай, вдруг сразу и отпустит. Врочем, подозреваю, потребителям акимовых и замятиных уже ничего не поможет.
А знаете, откуда взялся этот обратный маятник?
Дело было так: гуталин на "большаке" заявил ( http://bolshoyforum.org/forum/... ):
Ну, гуталин вроде учился в универе и делал в свое время лабораторку с оборотным маяником, но остальная тамошняя публика "путает кеш с хешем" ©, и ярема тут же откликнулся ( http://bolshoyforum.org/forum/... ):
И всё заверте...
ER*> Полудрагоценный, тебе уже открытым текстом сказали - математическое описание движения обратного маятника ничем не отличается от описания движения "обычного" физического маятника. В Интернете полно такого материала. Хоть в Википедии. Почитай, вдруг сразу и отпустит. Врочем, подозреваю, потребителям акимовых и замятиных уже ничего не поможет.

А знаете, откуда взялся этот обратный маятник?
Дело было так: гуталин на "большаке" заявил ( http://bolshoyforum.org/forum/... ):
Нет, Крош, не получается. ER* правильно говорит - таким способом их за руку не поймать.
Проблема вот в чём. Когда мы видим видеозапись, мы знаем, с какой частотой кадров мы её смотрим, но не знаем, с какой частотой кадров она была сделана. Соответственно, если при земной гравитации скорость съёмки увеличить в 2.45 раза (корень квадратный из 6), то, при воспроизведении записи с нормальной скоростью всё будет выглядеть так же, как и снятое при гравитации в 6 раз меньше земной. Маятник будет колебаться с периодом в 2.45 раза больше - точно так же, как при съёмке с нормальной частотой и пониженной в 6 раз гравитацией. Брошенный камень будет лететь по той же траектории - если камень бросить со скоростью 2.45V0 при гравитации в 1g, то он поднимется на ту же высоту и пролетит такое же расстояние, как и брошенный со скоростью V0 при гравитации 1/6g - потому что в их уравнения входит V02/g. И экранное время полёта будет как надо соответствовать экранной скорости полёта камня.
Нужен какой-то независимый процесс, который протекает с известной скоростью, по которому можно было бы откалибровать скорость съёмки.
Как вариант можно было бы использовать оборотный маятник для гравиметрии и заснять этот процесс, но у американских шулеров и маятник будет шулерским, так что не годится. Нужен какой-то процесс, который они не могли бы подделать.
Ну, гуталин вроде учился в универе и делал в свое время лабораторку с оборотным маяником, но остальная тамошняя публика "путает кеш с хешем" ©, и ярема тут же откликнулся ( http://bolshoyforum.org/forum/... ):
Обратным маятником можно промоделировать процесс хождения. Можно сделать хронометрию прогулок звездонавтов не прыжками, а обычными шагами. Правда, такие случаи редки. И кстати, есть процесс, который они подделать не смогли. Или, просто, в свое время над этим не задумались. Этот процесс - сохранение равновесия при лунном тяготении.
И всё заверте...

A Lannister always pays his debts.


V.a.C.> Ты лучше за этим к глистунгу aka галахический поц - нынче на хозяйстве он за клоуна - уж не откажет же подельничку, засасывающему две подряд, но исключающему третью 
Ва-ха-ха, да ты решительно всё перепутал. Я же здесь по контрамарке. На твоём бенефисе. А кинцо своё про пастора Шлага для лунопедов прибереги, как видеоиллюстрацию того, как ты здесь салазки загибал.

Ва-ха-ха, да ты решительно всё перепутал. Я же здесь по контрамарке. На твоём бенефисе. А кинцо своё про пастора Шлага для лунопедов прибереги, как видеоиллюстрацию того, как ты здесь салазки загибал.



V.a.C.> Так вы разберитесь в двух-то соснах - или
Так ты уже разобрался с Gravity Probe B? Нашел материальчик? Или заврался и в кусты? Ну "смелость" опровергателей давно известна.
V.a.C.> Если оно пустое - ваше пространство, то в чем распространяются световые и радио волны? Это волны чего - пустоты? А, господа пелевины!?
Если у тебя в твоей черепушке может уместиться только пространство или заполненное шариками материи или не заполненное, то это твои личные проблемы. У физиков таких проблем нет.
V.a.C.> А если оно не пустое, т.е.является материальной средой для их распространения с постоянной для данной среды скоростью С, то где тогда нахрен оказывается принцип относительности ИСО, если эта самая среда (эфир, физический вакуум и т.д.) как раз и является той самой нулевой (привилегированной) ИСО от которой и шарахаются, как черт от святого причастия, члены секты релятивистов?
Никто и не шарахается. Скорость света именно что постоянна для данной среды и именно что одинакова для всех ИСО. Просто ты своим мозжечком не способен это понять. Поэтому тебе и кажется что жыды специально придумали непонятную для тебя теорию, чтобы захватить мир.
Подсказка - курить преобразования Лоренца. Но боюсь что не в коня корм.
Так ты уже разобрался с Gravity Probe B? Нашел материальчик? Или заврался и в кусты? Ну "смелость" опровергателей давно известна.
V.a.C.> Если оно пустое - ваше пространство, то в чем распространяются световые и радио волны? Это волны чего - пустоты? А, господа пелевины!?
Если у тебя в твоей черепушке может уместиться только пространство или заполненное шариками материи или не заполненное, то это твои личные проблемы. У физиков таких проблем нет.
V.a.C.> А если оно не пустое, т.е.является материальной средой для их распространения с постоянной для данной среды скоростью С, то где тогда нахрен оказывается принцип относительности ИСО, если эта самая среда (эфир, физический вакуум и т.д.) как раз и является той самой нулевой (привилегированной) ИСО от которой и шарахаются, как черт от святого причастия, члены секты релятивистов?
Никто и не шарахается. Скорость света именно что постоянна для данной среды и именно что одинакова для всех ИСО. Просто ты своим мозжечком не способен это понять. Поэтому тебе и кажется что жыды специально придумали непонятную для тебя теорию, чтобы захватить мир.

Подсказка - курить преобразования Лоренца. Но боюсь что не в коня корм.


V.a.C.> выдумывается некоторая несуществующая в реальности условность, типа тени от объекта, но без самого объекта
А кто Вам сказал, что не бывает тени от объекта без самого объекта? "Здравый смысл"? С чего Вы взяли, что эта "аксиома от здравого смысла" непременно верна?
V.a.C.> Правда потом во все стороны начинают лезть гвозди и нитки от неряшливо сшитой "θеории"
Гвозди и нитки в студию!
А кто Вам сказал, что не бывает тени от объекта без самого объекта? "Здравый смысл"? С чего Вы взяли, что эта "аксиома от здравого смысла" непременно верна?
V.a.C.> Правда потом во все стороны начинают лезть гвозди и нитки от неряшливо сшитой "θеории"
Гвозди и нитки в студию!


Сергей-4030>> Эйнштейново пространство-время является математической моделью
Yuriy> Тем не менее, энергию оно несет (в виде гравитационных волн), и информацию может ими же передавать.
Модель - это схема. Пассажиров в метро перевозят поезда, а не схема метрополитена.
Yuriy> Тем не менее, энергию оно несет (в виде гравитационных волн), и информацию может ими же передавать.
Модель - это схема. Пассажиров в метро перевозят поезда, а не схема метрополитена.
Не ошибается тот, кто ничего не делает.




Дадхи на БФ упорствует в своем заблуждении про Акимова. Даже несмотря на доказательства через компютерную программу, что должно быть ему близко.  Какбе специально для нашего белорусского друга:
Какбе специально для нашего белорусского друга:
Подумалось, а не замахнутся ли нам на нашего, понимаете ли, Альберта Германовича, и не провести мысленный эксперимент?
Пусть по горизонтальной оси в указанном направлении движется со скоростью v транспортное средство, которое выпускает пассажиров в точках C (Cate) и D (Dadhi) с интервалом времени δt. Пассажиры движутся к конечной цели своего путешествия - к точке А (Apollo). Скорость пешеходов u. Нужно найти с каким интервалом δt' пассажиры появятся в точке А.
Очевидно, для малых интервалов времени δt путевая разница для Cate и Dadhi будет составлять (в первом приближении, с линейными членами) - отрезок |CB|.
|CB| = |CD| * cos(Альфа) = v * δt * cos(Альфа) ;
Чтобы пройти свою часть пути, Cate понадобится больше на |CB|/u = v * δt * cos(Альфа)/u времени чем Dadhi. С другой стороны, Dadhi стартует нa δt позже, чем Cate. Значит, интервал δt' между их появлением в А можно записать как разницу этих интервалов:
δt' = δt - v * δt * cos(Альфа)/u ;
или
δt' = δt * (1 - ß * cos(Альфа)) ;
- где ß = v/u.
Как видим, в нашем нехитром мысленном эксперименте, для интервалов приходов наших пассажиров, - а, следовательно, и периодов сигналов или волн - на приёмной стороне А выполняется классический эффект Доплера. У акимовых, замятиных и примкнувших к ним колоколовых нашему углу Альфа соответствует φ, а конечное выражение у них (5) :
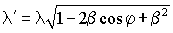 (5)
(5)
Ни разу не совпадает с нашим результатом. Как известно, мысленный эксперимент в физике - это типа аналог доказательства теоремы или леммы в математике. Таким образом, г-да Акимов, Колоколов, Замятин, a так же их почитатели дружно идут понятно куда.
 Какбе специально для нашего белорусского друга:
Какбе специально для нашего белорусского друга: Подумалось, а не замахнутся ли нам на нашего, понимаете ли, Альберта Германовича, и не провести мысленный эксперимент?
Пусть по горизонтальной оси в указанном направлении движется со скоростью v транспортное средство, которое выпускает пассажиров в точках C (Cate) и D (Dadhi) с интервалом времени δt. Пассажиры движутся к конечной цели своего путешествия - к точке А (Apollo). Скорость пешеходов u. Нужно найти с каким интервалом δt' пассажиры появятся в точке А.
Очевидно, для малых интервалов времени δt путевая разница для Cate и Dadhi будет составлять (в первом приближении, с линейными членами) - отрезок |CB|.
|CB| = |CD| * cos(Альфа) = v * δt * cos(Альфа) ;
Чтобы пройти свою часть пути, Cate понадобится больше на |CB|/u = v * δt * cos(Альфа)/u времени чем Dadhi. С другой стороны, Dadhi стартует нa δt позже, чем Cate. Значит, интервал δt' между их появлением в А можно записать как разницу этих интервалов:
δt' = δt - v * δt * cos(Альфа)/u ;
или
δt' = δt * (1 - ß * cos(Альфа)) ;
- где ß = v/u.
Как видим, в нашем нехитром мысленном эксперименте, для интервалов приходов наших пассажиров, - а, следовательно, и периодов сигналов или волн - на приёмной стороне А выполняется классический эффект Доплера. У акимовых, замятиных и примкнувших к ним колоколовых нашему углу Альфа соответствует φ, а конечное выражение у них (5) :
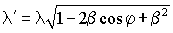 (5)
(5)Ни разу не совпадает с нашим результатом. Как известно, мысленный эксперимент в физике - это типа аналог доказательства теоремы или леммы в математике. Таким образом, г-да Акимов, Колоколов, Замятин, a так же их почитатели дружно идут понятно куда.



Это сообщение редактировалось 19.01.2012 в 18:54
Сергей-4030>> Эйнштейново пространство-время является математической моделью, которая по (принципиально) неизвестным нам причинам хорошо описывает поведение реальных вещей.
Yuriy> Тем не менее, энергию оно несет (в виде гравитационных волн), и информацию может ими же передавать.
Математическая модель никаких энергий не несет. Это абстракция, она существует только в голове субъекта. Вам так сложно понять, что модель != реальности? Вот посмотрите на физическую карту, видите изогипсы (линии одинаковых высот)? Вы понимаете, что этих линий на местности на самом деле нет? Точки с одинаковой высотой - есть, но через них на местности никаких линий не проведено. Эти линии - отображение модели. Неужели это так сложно? Точно так же с полями. Скажем, электростатическое поле - просто модель, предсказывающая, что если в окрестностях заряда X поместить заряд Y, то возникнет сила равная f(x,y,r) = <чему-то там>. Плюс ее в том, что она хорошо предсказывает результат. Но при этом собственно "поля" нет, никаких линий в пространстве не проведено. И говорить, что "сила возникает потому, что существует поле блаблабла" - это масло масляное.
Yuriy> Тем не менее, энергию оно несет (в виде гравитационных волн), и информацию может ими же передавать.
Математическая модель никаких энергий не несет. Это абстракция, она существует только в голове субъекта. Вам так сложно понять, что модель != реальности? Вот посмотрите на физическую карту, видите изогипсы (линии одинаковых высот)? Вы понимаете, что этих линий на местности на самом деле нет? Точки с одинаковой высотой - есть, но через них на местности никаких линий не проведено. Эти линии - отображение модели. Неужели это так сложно? Точно так же с полями. Скажем, электростатическое поле - просто модель, предсказывающая, что если в окрестностях заряда X поместить заряд Y, то возникнет сила равная f(x,y,r) = <чему-то там>. Плюс ее в том, что она хорошо предсказывает результат. Но при этом собственно "поля" нет, никаких линий в пространстве не проведено. И говорить, что "сила возникает потому, что существует поле блаблабла" - это масло масляное.


Сергей-4030> Математическая модель никаких энергий не несет.
В таком случае поле - не математическая абстракция, ибо несет энергию.
Сергей-4030> Это абстракция, она существует только в голове субъекта. Вам так сложно понять, что модель != реальности? Вот посмотрите на физическую карту, видите изогипсы (линии одинаковых высот)? Вы понимаете, что этих линий на местности на самом деле нет?
Вы хотите этим опровергнуть существование местности?
Поле не перестает существовать от того, что все его описания являются абстрактными моделями.
Сергей-4030> Скажем, электростатическое поле - просто модель, предсказывающая, что если в окрестностях заряда X поместить заряд Y, то возникнет сила равная f(x,y,r) = . Плюс ее в том, что она хорошо предсказывает результат.
Предсказывает результат не поле, а математическая модель в голове математика.
Поле же представляется собой самостоятельную сущность - точно так же как электрон имеет свою собственную энергию и может нести информацию, точно так же и поле имеет энергию и несет в себе информацию.
По Вашей логике точно так же не существует и зарядов: по Вашему, заряд Х это не объект, а "математическая модель, объясняющая силу f(x,y,r) = ...". По Вашей логике вообще не существует физических объектов, есть только "модели"...
Сергей-4030> Но при этом собственно "поля" нет, никаких линий в пространстве не проведено.
Не переводите стрелки на демогогию. Речь идет не о математической модели. Речь идет о физическом объекте.
Поясню разницу. Есть заряд, его наличие можно обнаружить по действию на другие заряды. Заряд - это объект. Его наличие дано нам в ощущениях, он реально существует.
А вот математические модели, описывающие, как заряд действует на заряд могут быть разные, модель физика Петрова, модель физика Иванова... В отличие от заряда они реально не существуют, не даны в ощущениях и являются математическими абстракциями.
Так же и электромагнитная волна, фотон - она либо есть, либо ее нет, и Вы постоянно наблюдаете в ощущениях фотоны. А вот то, как фотоны действуют на заряд - тут чистая математическая абстракция.
Сергей-4030> И говорить, что "сила возникает потому, что существует поле блаблабла" - это масло масляное.
Вопрос не в том, "почему сила действует", вопрос в том, какие объекты взаимодействуют.
Короче, есть ряд взаимодействующих по определенным правилам объектов:
1) Заряды.
2) Электромагнитные волны.
И то и другое несет энергию, и то и другое несет информацию, и то, и другое воздействует на пробный заряд - но Вы почему-то отказываете в реальности электромагнитным волнам, называя их "абстрактной моделью" (а почему не наоборот?).
Поведение каждого заряда определяется и наличием других зарядов, и наличием электромагнитных волн, но почему-то Вы считаете заряды за объекты а волны за "абстрактные модели, придуманные для объяснения сил действующих на заряды". А почему не наоборот? Заряженные объекты - это "абстрактные модели, придуманные для объяснения поведения электромагнитных волн" (кстати, электромагнитные волны, в отличие от заряженных объектов, электромагнитные волны даны нам в ощущениях непосредственно).
Значит так. Модель тем и отличается от объекта, что ее можно заменить альтернативной, выдумать ошибочную, вообще об этом не думать - ничего не изменится.
Вот Земля вращается вокруг Солнца. Солнце - явно физический объект, если его изъять, Земля перестанет нарезать круги. Солнце дано нам в ощущениях.
А вот теории гравитации, что Эйнштейнова в неэвклидовом пространстве, что Ньютонова в эвклидовом, что все карты гравитационного поля с изогравами - все это модели, они не влияют на поведение объектов. Невозможно проверить "наличие" или "отсутствие" абстрактного построения в системе Земля-Солнце, т.к. оно не является объектом, влияющим на что-либо в системе.
А вот электромагнитные волны - реально существующие объекты. Когда электромагнитный сигнал летит между точками, в нем сосредоточена информация, и энергия тоже. Изъять его нельзя - это все равно, что изъять Солнце из Солнечной Системы, наличие или отсутствие электромагнитной волны влияет на поведение заряженных частиц.
А вот электромагнитные теории, описывающие взаимодействие реально существующих объектов - заряженных предметов и электромагнитных волн - не существуют в реальности.
В таком случае поле - не математическая абстракция, ибо несет энергию.
Сергей-4030> Это абстракция, она существует только в голове субъекта. Вам так сложно понять, что модель != реальности? Вот посмотрите на физическую карту, видите изогипсы (линии одинаковых высот)? Вы понимаете, что этих линий на местности на самом деле нет?
Вы хотите этим опровергнуть существование местности?
Поле не перестает существовать от того, что все его описания являются абстрактными моделями.
Сергей-4030> Скажем, электростатическое поле - просто модель, предсказывающая, что если в окрестностях заряда X поместить заряд Y, то возникнет сила равная f(x,y,r) = . Плюс ее в том, что она хорошо предсказывает результат.
Предсказывает результат не поле, а математическая модель в голове математика.
Поле же представляется собой самостоятельную сущность - точно так же как электрон имеет свою собственную энергию и может нести информацию, точно так же и поле имеет энергию и несет в себе информацию.
По Вашей логике точно так же не существует и зарядов: по Вашему, заряд Х это не объект, а "математическая модель, объясняющая силу f(x,y,r) = ...". По Вашей логике вообще не существует физических объектов, есть только "модели"...
Сергей-4030> Но при этом собственно "поля" нет, никаких линий в пространстве не проведено.
Не переводите стрелки на демогогию. Речь идет не о математической модели. Речь идет о физическом объекте.
Поясню разницу. Есть заряд, его наличие можно обнаружить по действию на другие заряды. Заряд - это объект. Его наличие дано нам в ощущениях, он реально существует.
А вот математические модели, описывающие, как заряд действует на заряд могут быть разные, модель физика Петрова, модель физика Иванова... В отличие от заряда они реально не существуют, не даны в ощущениях и являются математическими абстракциями.
Так же и электромагнитная волна, фотон - она либо есть, либо ее нет, и Вы постоянно наблюдаете в ощущениях фотоны. А вот то, как фотоны действуют на заряд - тут чистая математическая абстракция.
Сергей-4030> И говорить, что "сила возникает потому, что существует поле блаблабла" - это масло масляное.
Вопрос не в том, "почему сила действует", вопрос в том, какие объекты взаимодействуют.
Короче, есть ряд взаимодействующих по определенным правилам объектов:
1) Заряды.
2) Электромагнитные волны.
И то и другое несет энергию, и то и другое несет информацию, и то, и другое воздействует на пробный заряд - но Вы почему-то отказываете в реальности электромагнитным волнам, называя их "абстрактной моделью" (а почему не наоборот?).
Поведение каждого заряда определяется и наличием других зарядов, и наличием электромагнитных волн, но почему-то Вы считаете заряды за объекты а волны за "абстрактные модели, придуманные для объяснения сил действующих на заряды". А почему не наоборот? Заряженные объекты - это "абстрактные модели, придуманные для объяснения поведения электромагнитных волн" (кстати, электромагнитные волны, в отличие от заряженных объектов, электромагнитные волны даны нам в ощущениях непосредственно).
Значит так. Модель тем и отличается от объекта, что ее можно заменить альтернативной, выдумать ошибочную, вообще об этом не думать - ничего не изменится.
Вот Земля вращается вокруг Солнца. Солнце - явно физический объект, если его изъять, Земля перестанет нарезать круги. Солнце дано нам в ощущениях.
А вот теории гравитации, что Эйнштейнова в неэвклидовом пространстве, что Ньютонова в эвклидовом, что все карты гравитационного поля с изогравами - все это модели, они не влияют на поведение объектов. Невозможно проверить "наличие" или "отсутствие" абстрактного построения в системе Земля-Солнце, т.к. оно не является объектом, влияющим на что-либо в системе.
А вот электромагнитные волны - реально существующие объекты. Когда электромагнитный сигнал летит между точками, в нем сосредоточена информация, и энергия тоже. Изъять его нельзя - это все равно, что изъять Солнце из Солнечной Системы, наличие или отсутствие электромагнитной волны влияет на поведение заряженных частиц.
А вот электромагнитные теории, описывающие взаимодействие реально существующих объектов - заряженных предметов и электромагнитных волн - не существуют в реальности.


Это сообщение редактировалось 20.01.2012 в 03:02
Короче говоря, есть объекты и есть модели для предсказывания поведения объектов.
Например, есть Солнце и Меркурий - реально существующие объекты. И есть ОТО - модель, позволяющая хорошо предсказать движение Меркурия, но не больше. Но абсолютно нелепо утверждать, что Солнце - это не материальный объект, а "модель для предсказания движения Меркурия".
Точно так же и электромагнитные волны - такие же реально существующие объекты, взаимодействующие с другими реально взаимодействующими объектами, чего нельзя сказать насчет электродинамики, которая является не объектом, а моделью, предсказывающей поведение системы из ряда объектов - носителей зарядов и электромагнитных волн.
Например, есть Солнце и Меркурий - реально существующие объекты. И есть ОТО - модель, позволяющая хорошо предсказать движение Меркурия, но не больше. Но абсолютно нелепо утверждать, что Солнце - это не материальный объект, а "модель для предсказания движения Меркурия".
Точно так же и электромагнитные волны - такие же реально существующие объекты, взаимодействующие с другими реально взаимодействующими объектами, чего нельзя сказать насчет электродинамики, которая является не объектом, а моделью, предсказывающей поведение системы из ряда объектов - носителей зарядов и электромагнитных волн.


Общие сведения об электромагнитном поле - Физические явления
Электромагнитное поле – это особый вид материи, принципиально отличный от вещества. В
// binomes.net
Электромагнитное поле – это особый вид материи, принципиально отличный от вещества. В зависимости от физических условий, оно проявляет себя в неразрывном единстве со своими источниками, с зарядами и токами, но оно может существовать и в свободном состоянии без связи с ними как самостоятельный объект.
Обладая массой, энергией и импульсом, электромагнитное поле во взаимодействии с зарядами и токами проявляют себя как реальный объект взаимодействия. Подобным же образом электромагнитное поле проявляет себя и во взаимодействии с частицами вещества, в силу чего своим воздействием на вещество оно фактически определяет его электромагнитное состояние.
P.S. Хоть убейте, не могу понять разницу между лучом света и любым другим материальным объектом.


Yuriy> Поле не перестает существовать от того, что все его описания являются абстрактными моделями.
Поле - это и есть абстрактная модель, которая описывает некую реальность. Реальность одна, моделей может быть много. Поле - одна из моделей.
Поле - это и есть абстрактная модель, которая описывает некую реальность. Реальность одна, моделей может быть много. Поле - одна из моделей.
Не ошибается тот, кто ничего не делает.




Yuriy> Поясню разницу. Есть заряд, его наличие можно обнаружить по действию на другие заряды. Заряд - это объект. Его наличие дано нам в ощущениях, он реально существует.
Я читаю текст, написанный вами. Выходит вы и ваше сознание даны мне в ощущениях. Получается, что ваше сознание - материально.
Я читаю текст, написанный вами. Выходит вы и ваше сознание даны мне в ощущениях. Получается, что ваше сознание - материально.

Не ошибается тот, кто ничего не делает.




Copyright © Balancer 1997..2018
Создано 13.03.2011
Связь с владельцами и администрацией сайта: anonisimov@gmail.com, rwasp1957@yandex.ru и admin@balancer.ru.
Создано 13.03.2011
Связь с владельцами и администрацией сайта: anonisimov@gmail.com, rwasp1957@yandex.ru и admin@balancer.ru.
/6561348.png)
 Viewer aka Catechesis
Viewer aka Catechesis

 инфо
инфо инструменты
инструменты
 Сергей-4030
Сергей-4030


 ER*
ER*







 7-40
7-40

