-
![[image]](https://www.balancer.ru/cache/sites/e/p/epizodsspace.testpilot.ru/bibl/ejeg/1974/128x128-crop/74-2.jpg)
Прохожелогия
Теги:
п314159>
п314159> есть однако и другая версия - Пустынский просто не знаком с особенностями применения разных методов для расчета функций гармонического вида.
Дык куда мне, я же не математик.
п314159> Я когда-то мучился с многоатомной молекулой с упругими связями Так я б тебе рассказал чего стоит этот Рунге в базарный день.
Так я б тебе рассказал чего стоит этот Рунге в базарный день.
Не, ты мне про свои мучения не заливай. Ты сказал, что ""расходимость" расчета этим методом <Адамса> уравнения вида f`(x)=sin(x) не наблюдается на любом отрезке времени. Как угодно долгом. В отличие от Эйлера, Рунге-Кутта и иже с ними". Мне было бы страшно любопытно услышать обоснования сего утверждения.
п314159>Пока однажды не прочел в коментах к фортрану для библиотеки Рунге-кутта. Там было жирным по белому написано - не применяется для упругих связей жескости в переводе на одну выше К=10000.
Во-первых, на каком языке написано последнее предложение? К - это, наверное, тоже "общепринятая терминология математическая"?
 Во-вторых, если ты повествуешь об универсальной библиотеке подпрограмм, как там могли упоминаться какие-то связи с какой-то жёсткостью? В-третьих, к чему ты вообще завёл эту песТню? Прохожий, чем больше ты рассказываешь, тем глубже вязнешь.
Во-вторых, если ты повествуешь об универсальной библиотеке подпрограмм, как там могли упоминаться какие-то связи с какой-то жёсткостью? В-третьих, к чему ты вообще завёл эту песТню? Прохожий, чем больше ты рассказываешь, тем глубже вязнешь. 
п314159> Хотя Адамс считает пружинный "маятник" хочь убейся "сутками". Про особенности Адамса и отличия в ньюансах от Рунге-Кутта можно диссертации писать. А на Рунге-Штирлице у меня эта молекула улетала в соседнюю галактику уже на ~тысячном шаге. Правда я по-приколу и "молекулу" взял "жестокую" - там была сотня элементов
у меня эта молекула улетала в соседнюю галактику уже на ~тысячном шаге. Правда я по-приколу и "молекулу" взял "жестокую" - там была сотня элементов  А вот на Адамсе не улетала
А вот на Адамсе не улетала 
Ой, это что, упражнения по экспериментальной математике?
 Сморозив, что метод Адамса имеет какие-то принципиальные отличия от Рунге-Кутта в отношении расходимости при гармонических членах в дифуре, ты решил попытаться обосновать это тем, что некая конкретная реализация в одном случае фурычила, а в другом нет?! Нет уж - нет уж, математик ты наш великий. Изволь теперь представить строгое доказательство, а не байки о криворуком вычислителе.
Сморозив, что метод Адамса имеет какие-то принципиальные отличия от Рунге-Кутта в отношении расходимости при гармонических членах в дифуре, ты решил попытаться обосновать это тем, что некая конкретная реализация в одном случае фурычила, а в другом нет?! Нет уж - нет уж, математик ты наш великий. Изволь теперь представить строгое доказательство, а не байки о криворуком вычислителе. 
п314159>
п314159> конечно не понял. Потому что оператор О. а М - некая пропорциональность в виде числа
Я о чём и говорю. Понять такие вещи ты просто не мог.
п314159> ну хорошо, что ты хоть сейчас это усвоил. Еще пару дней назад для тебя это было китайской азбукой. особенно запись через степень шага h
особенно запись через степень шага h 
Ну дык! Приходит Прохожий, пишет всякую галиматью, у него переспрашиваешь - он говорит, что валяется под столом и что это "общепринятая терминология математическая". И лишь потом, методом последовательных приближений, оказывается, что за таковую Прохожий выдал первое попавшееся в книжке и даже не понятое им.
п314159> Хотя твое кудахтанье про школьные справочники просто смешно. Лично у меня оно встречается в курсе дифференциального и интегрального исчесления некоего гражданина Пискунова. Для высших учебных заведений
Прохожий, "кудахтанье" - это моё слово, я знаю, что оно тебе нравится, но изволь не воровать. То, что такое обозначение присутствует в учебном курсе для вузов, полностью соответствует моим словам "запись через пропорцию встречается чаще в простых справочниках - школьных или инженерных". Ты слово "инженерных" заметил? Инженеров готовят в вузах обычно.
То, что такое обозначение присутствует в учебном курсе для вузов, полностью соответствует моим словам "запись через пропорцию встречается чаще в простых справочниках - школьных или инженерных". Ты слово "инженерных" заметил? Инженеров готовят в вузах обычно.  И как раз в прикладных курсах чаще встречаются подобного рода обозначения.
И как раз в прикладных курсах чаще встречаются подобного рода обозначения.
п314159>
п314159> опять звездишь??? для задач двух- и Н-тел разница между полярные/прямоугольные/хоть цилиндрические никакая. Количество уравнений от этого не меняется. Сколько степеней свободы - столько и решать.
Да что ты ерунду мне порешь? Ты хоть немного думай, прежде чем галиматью писать. В задаче 2-х тел сколько степеней свободы? 6 было испокон веков. Ну так вот в произвольных прямоугольных координатах ИСО и будет 6 уравнений 2-го порядка. Простое преобразование координат "сдвиг-поворот" уменьшит число уравнений до 2-х уравнений 2-го порядка. А переход к координатам "обратный радиус-вектор - угол" оставит трансцендентное уравнение Кеплера да уравнение Бине, которое даже ты сможешь, быть может, решить аналитически за шесть часов страшных мучений.
"Разница никакая"... Слушай, если только перечислять типы координат, которые применяются в небесной механике, то будет нехилый список. Бывают, знаешь, такие особо извращённые - вращающиеся всякими хитрыми способами, или с разными комбинациями классических элементов. Усякие координаты Нехвилла и тому подобные страшные вещи. Их не зря придумали, Прохожий, не зря.
п314159> тебе Факир совсем про другое сказал. И с точностью до наоборот
Щас мы у него спросим.
А то теперь ты говоришь, что это метод Адамса 4-го порядка. Ну а какая принципиальная разница с точки зрения расходимостей в отношении "уравнения вида f`(x)=sin(x)" между методами Адамса и Рунге-Кутта? Значит, ты снова врёшь и лажаешь.
п314159> есть однако и другая версия - Пустынский просто не знаком с особенностями применения разных методов для расчета функций гармонического вида.
Дык куда мне, я же не математик.

п314159> Я когда-то мучился с многоатомной молекулой с упругими связями
 Так я б тебе рассказал чего стоит этот Рунге в базарный день.
Так я б тебе рассказал чего стоит этот Рунге в базарный день.Не, ты мне про свои мучения не заливай. Ты сказал, что ""расходимость" расчета этим методом <Адамса> уравнения вида f`(x)=sin(x) не наблюдается на любом отрезке времени. Как угодно долгом. В отличие от Эйлера, Рунге-Кутта и иже с ними". Мне было бы страшно любопытно услышать обоснования сего утверждения.

п314159>Пока однажды не прочел в коментах к фортрану для библиотеки Рунге-кутта. Там было жирным по белому написано - не применяется для упругих связей жескости в переводе на одну выше К=10000.
Во-первых, на каком языке написано последнее предложение? К - это, наверное, тоже "общепринятая терминология математическая"?

 Во-вторых, если ты повествуешь об универсальной библиотеке подпрограмм, как там могли упоминаться какие-то связи с какой-то жёсткостью? В-третьих, к чему ты вообще завёл эту песТню? Прохожий, чем больше ты рассказываешь, тем глубже вязнешь.
Во-вторых, если ты повествуешь об универсальной библиотеке подпрограмм, как там могли упоминаться какие-то связи с какой-то жёсткостью? В-третьих, к чему ты вообще завёл эту песТню? Прохожий, чем больше ты рассказываешь, тем глубже вязнешь. 
п314159> Хотя Адамс считает пружинный "маятник" хочь убейся "сутками". Про особенности Адамса и отличия в ньюансах от Рунге-Кутта можно диссертации писать. А на Рунге-Штирлице
 у меня эта молекула улетала в соседнюю галактику уже на ~тысячном шаге. Правда я по-приколу и "молекулу" взял "жестокую" - там была сотня элементов
у меня эта молекула улетала в соседнюю галактику уже на ~тысячном шаге. Правда я по-приколу и "молекулу" взял "жестокую" - там была сотня элементов  А вот на Адамсе не улетала
А вот на Адамсе не улетала 
Ой, это что, упражнения по экспериментальной математике?

 Сморозив, что метод Адамса имеет какие-то принципиальные отличия от Рунге-Кутта в отношении расходимости при гармонических членах в дифуре, ты решил попытаться обосновать это тем, что некая конкретная реализация в одном случае фурычила, а в другом нет?! Нет уж - нет уж, математик ты наш великий. Изволь теперь представить строгое доказательство, а не байки о криворуком вычислителе.
Сморозив, что метод Адамса имеет какие-то принципиальные отличия от Рунге-Кутта в отношении расходимости при гармонических членах в дифуре, ты решил попытаться обосновать это тем, что некая конкретная реализация в одном случае фурычила, а в другом нет?! Нет уж - нет уж, математик ты наш великий. Изволь теперь представить строгое доказательство, а не байки о криворуком вычислителе. 
п314159>
Ты даже не понял, почему я назвал М оператором. Ладно, я тебе расскажу. Общепринятая запись в таком случае - как раз операторная, а именно O(h^k), с использованием оператора O.
п314159> конечно не понял. Потому что оператор О. а М - некая пропорциональность в виде числа
Я о чём и говорю. Понять такие вещи ты просто не мог.

п314159> ну хорошо, что ты хоть сейчас это усвоил. Еще пару дней назад для тебя это было китайской азбукой.
 особенно запись через степень шага h
особенно запись через степень шага h 
Ну дык! Приходит Прохожий, пишет всякую галиматью, у него переспрашиваешь - он говорит, что валяется под столом и что это "общепринятая терминология математическая". И лишь потом, методом последовательных приближений, оказывается, что за таковую Прохожий выдал первое попавшееся в книжке и даже не понятое им.

п314159> Хотя твое кудахтанье про школьные справочники просто смешно. Лично у меня оно встречается в курсе дифференциального и интегрального исчесления некоего гражданина Пискунова. Для высших учебных заведений

Прохожий, "кудахтанье" - это моё слово, я знаю, что оно тебе нравится, но изволь не воровать.
 То, что такое обозначение присутствует в учебном курсе для вузов, полностью соответствует моим словам "запись через пропорцию встречается чаще в простых справочниках - школьных или инженерных". Ты слово "инженерных" заметил? Инженеров готовят в вузах обычно.
То, что такое обозначение присутствует в учебном курсе для вузов, полностью соответствует моим словам "запись через пропорцию встречается чаще в простых справочниках - школьных или инженерных". Ты слово "инженерных" заметил? Инженеров готовят в вузах обычно.  И как раз в прикладных курсах чаще встречаются подобного рода обозначения.
И как раз в прикладных курсах чаще встречаются подобного рода обозначения.п314159>
Но на точность решения выбор между полярными и прямоугольными влияет сплошь и рядом, а порой очень сильно - например в задачах небесной механики. И в отдельных случаях это влияние может быть очень сильным
п314159> опять звездишь??? для задач двух- и Н-тел разница между полярные/прямоугольные/хоть цилиндрические никакая. Количество уравнений от этого не меняется. Сколько степеней свободы - столько и решать.
Да что ты ерунду мне порешь? Ты хоть немного думай, прежде чем галиматью писать. В задаче 2-х тел сколько степеней свободы? 6 было испокон веков. Ну так вот в произвольных прямоугольных координатах ИСО и будет 6 уравнений 2-го порядка. Простое преобразование координат "сдвиг-поворот" уменьшит число уравнений до 2-х уравнений 2-го порядка. А переход к координатам "обратный радиус-вектор - угол" оставит трансцендентное уравнение Кеплера да уравнение Бине, которое даже ты сможешь, быть может, решить аналитически за шесть часов страшных мучений.

"Разница никакая"... Слушай, если только перечислять типы координат, которые применяются в небесной механике, то будет нехилый список. Бывают, знаешь, такие особо извращённые - вращающиеся всякими хитрыми способами, или с разными комбинациями классических элементов. Усякие координаты Нехвилла и тому подобные страшные вещи. Их не зря придумали, Прохожий, не зря.
п314159> тебе Факир совсем про другое сказал. И с точностью до наоборот
Щас мы у него спросим.

Это сообщение редактировалось 12.09.2005 в 14:47
Прохожий:
О, пока писал, Факир сам у себя спросил и ответил. И про Пискунова тоже. Я вообще-то этот справочник лишь изредка видел и едва ли открывал, но если он действительно для ВТУЗов, то мои слова "А запись через пропорцию встречается чаще в простых справочниках - школьных или Но это уж ты сам, извини...
Но это уж ты сам, извини... 
О, пока писал, Факир сам у себя спросил и ответил. И про Пискунова тоже. Я вообще-то этот справочник лишь изредка видел и едва ли открывал, но если он действительно для ВТУЗов, то мои слова "А запись через пропорцию встречается чаще в простых справочниках - школьных или
инженерных
" оказались верны с точностью до буквы. А твои излияния "Хотя твое кудахтанье про школьные справочники просто смешно. Лично у меня оно встречается в курсе дифференциального и интегрального исчесления некоего гражданина Пискунова. Для высших учебных заведений" лишь подтверждают справедливость моей монополии на упоминание про твоё истерическое кудахтанье всякий раз, как ты в очередной раз сам себя подвергаешь истязаниям.  Но это уж ты сам, извини...
Но это уж ты сам, извини... 
аФон+> Ну, если 9 км в сек и угол нужный с его более широким коридором, перегрузки то уменьшатся?
п314159> это если угол нужный. Просто с уменьшением скорости отпадает надобность в цирках с двумя нырками и пр.
На какой скорости отпадает надобность в цирках с двумя нырками?
На 10 км в сек можно обойтись и получить вот такую точность?
п314159> это если угол нужный. Просто с уменьшением скорости отпадает надобность в цирках с двумя нырками и пр.
На какой скорости отпадает надобность в цирках с двумя нырками?
На 10 км в сек можно обойтись и получить вот такую точность?
Глава VIII. ВЕРХОМ НА «ЛУННОМ СКИТАЛЬЦЕ»После того как экипаж «Аполлона-16» приводнился менее чем в двух километрах от авианосца «Тикондерога», установив новый рекорд точности посадки для «Аполлонов»,
Это сообщение редактировалось 12.09.2005 в 16:25
п314159> опять звездишь??? для задач двух- и Н-тел разница между полярные/прямоугольные/хоть цилиндрические никакая. Количество уравнений от этого не меняется. Сколько степеней свободы - столько и решать. тебе Факир совсем про другое сказал. И с точностью до наоборот :angry: [»]
Прохожий, Факир уже подтвердил, что вы его поняли с точностью до наоборот
А вот что другие люди пишут на эту тему:
Это из "Atmospheric Reentry Modeling and Simulation" ( http://spacecraft.ssl.umd.edu/design_lib/JSRv39n4.entry_sim.pdf ) - статьи, специально посвященной численному моделированию процесса входа
Прохожий, Факир уже подтвердил, что вы его поняли с точностью до наоборот

А вот что другие люди пишут на эту тему:
The choice of the coordinate system is of major importance because it will influence the effectiveness of the simulation tool.
Это из "Atmospheric Reentry Modeling and Simulation" ( http://spacecraft.ssl.umd.edu/design_lib/JSRv39n4.entry_sim.pdf ) - статьи, специально посвященной численному моделированию процесса входа

Bell>> На ручном управлении? Зонды и на автомате неплохо входили в коридор, а с космонавтами - уж точно попали бы.
аФон+> Как космонавты могут помочь компьютеру управлять процессом входа в коридор? [»]
Вход в коридор обеспечивается заранее - путем соответствующих коррекций траектории. Компьютер на борту для этого не особо нужен - можно обойтись и наземным. "Аполлоны" выполняли последнюю коррекцию для входа в коридор за несколько часов до входа. См. The Apollo 15 Flight Journal - Splashdown Day .
При спуске тоже можно было обойтись и без компьютера в случае его отказа. На "Аполлонах" имелась независимая система мониторинга входа, которая показывала текущие параметры полета и позволяла управлять спуском вручную, основываясь на ее показаниях.
аФон+> Как космонавты могут помочь компьютеру управлять процессом входа в коридор? [»]
Вход в коридор обеспечивается заранее - путем соответствующих коррекций траектории. Компьютер на борту для этого не особо нужен - можно обойтись и наземным. "Аполлоны" выполняли последнюю коррекцию для входа в коридор за несколько часов до входа. См. The Apollo 15 Flight Journal - Splashdown Day .
Midcourse 7 is formally known as the Corridor Control Burn and is used to fine tune their approach into the narrow corridor of the atmosphere. While Endeavour is still well within the limits for a successful entry, tweaking the trajectory now will ensure that the Command Module will not have to perform extra maneuvers as the computer works to balance the optimal entry profile and targeting to the recovery force. The burn will be performed at 291:58:48.]
...
Public Affairs Officer - "This is Apollo Control at 288 hours, 5 minutes. Apollo 15 is 46,778 nautical miles [86,633 km] from Earth. Velocity: 8,622 feet per second [2,628 m/s]. We're 7 hours, 5 minutes from landing. Apollo 15 will perform the midcourse correction number 7. Looking right now at time very close to the Flight Plan. Midcourse [7 will occur] somewhere around 291 hours, 56 minutes. And it will be on the order of 5 feet per second [1.5 m/s]. We will use the Reaction Control System attitude thrusters on the Service Module for this midcourse. We will get some more tracking before we firm up the burn and the time. Tracking during the sleep period last night, while the spacecraft was in a stable trajectory, shows that the trajectory was perturbed somewhat during the maneuvering yesterday while the crew was performing some of the experiments and photography work. So a midcourse will be required. At 288 hours, 7 minutes, this is Mission Control, Houston."
При спуске тоже можно было обойтись и без компьютера в случае его отказа. На "Аполлонах" имелась независимая система мониторинга входа, которая показывала текущие параметры полета и позволяла управлять спуском вручную, основываясь на ее показаниях.
Прикреплённые файлы:
Это сообщение редактировалось 12.09.2005 в 16:19
п314159
втянувшийся
Факир -
процентов от чего??? Я вас уверяю, что разницы между полярными и декартовыми координатами никакой. Разница появляется там, где под "заменой" координат вы на самом деле сводите задачу к другой. То бишь вставляете кусок "физики" в "математику".
Я вас уверяю, что разницы между полярными и декартовыми координатами никакой. Разница появляется там, где под "заменой" координат вы на самом деле сводите задачу к другой. То бишь вставляете кусок "физики" в "математику".
Ну чтоб вы поняли - это тоже самое, как утверждать, что в килограммах задача решается хуже, чем скажем в фунтах или пудах
А вот когда вы задачу сводите к другой - тогда да.
ну это уже мастерство реализации. "загогулину" в любой задаче можно найти
ПУСТЫНСКИЙ -
твое высокомерие тут не уместно. Он Пискунов, а ты никто. Пустынский. Так что помолчи.
Лично у меня было два уравнения второго порядка. И его решения - две функции Y=Y(t) X=X(t). Все остальное - промежуточные результаты. Куда дальше будем упрощать??? в полярных тоже будет две координаты. Мы говорим о конкретной задаче, а не вообще
Ты на меня наехал, мол я выбрал не ту СК. ну и какую надо? чем полярка тут поможет? Давай вопрос ребром. ОК? :angry:
Пустынский, не строй из себя дурака. Ты еще недавно вообще не подозревал, что ошибку пишут через степень шага. Теперь ты начинаешь мол O(H4) ты теперь понял, а буквы Mh4 искал в Гугле? Ну ведь если бы ты хоть раз видел в жизни это выражение, ты бы так не кудахтал от удивления.
Ну ведь если бы ты хоть раз видел в жизни это выражение, ты бы так не кудахтал от удивления.
Называется индюк думал и в суп попал
в начале ты представишь строгое доказательство, что метод Адамса четвертого порядка (ты его записать хоть сможешь?) дает погрешность O(h4) или Mh4 (Ah4, Bh4, Kh4 ... ) а я уж потом подумаю
) а я уж потом подумаю 
Вероятно, при решении одной и той же задачи в полярных и декартовых, особенно при подобранной на скорую руку сетке, оно вполне может достигать и десятков процентов.
процентов от чего???
 Я вас уверяю, что разницы между полярными и декартовыми координатами никакой. Разница появляется там, где под "заменой" координат вы на самом деле сводите задачу к другой. То бишь вставляете кусок "физики" в "математику".
Я вас уверяю, что разницы между полярными и декартовыми координатами никакой. Разница появляется там, где под "заменой" координат вы на самом деле сводите задачу к другой. То бишь вставляете кусок "физики" в "математику".Ну чтоб вы поняли - это тоже самое, как утверждать, что в килограммах задача решается хуже, чем скажем в фунтах или пудах

А вот когда вы задачу сводите к другой - тогда да.

Казалось бы - есть углы Эйлера, ну или Крылова - можно считать, и никаких гвоздей. Оказалось, что не так всё просто - при использовании таких координат компы часто затыкались (при обнулении углов). Поэтому на "Энергии" ввели в употребление кватернионное описание, и оно сейчас вроде бы весьма широко используется - для компов самое то.
ну это уже мастерство реализации. "загогулину" в любой задаче можно найти

ПУСТЫНСКИЙ -
Я вообще-то этот справочник лишь изредка видел и едва ли открывал, но если он действительно для ВТУЗов, то мои слова "А запись через пропорцию встречается чаще в простых справочниках - школьных или инженерных" оказались верны с точностью до буквы.
твое высокомерие тут не уместно. Он Пискунов, а ты никто. Пустынский. Так что помолчи.

В задаче 2-х тел сколько степеней свободы? 6 было испокон веков. Ну так вот в произвольных прямоугольных координатах ИСО и будет 6 уравнений 2-го порядка. Простое преобразование координат "сдвиг-поворот" уменьшит число уравнений до 2-х уравнений 2-го порядка. А переход к координатам "обратный радиус-вектор - угол" оставит трансцендентное уравнение Кеплера да уравнение Бине
Лично у меня было два уравнения второго порядка. И его решения - две функции Y=Y(t) X=X(t). Все остальное - промежуточные результаты. Куда дальше будем упрощать??? в полярных тоже будет две координаты. Мы говорим о конкретной задаче, а не вообще

Ты на меня наехал, мол я выбрал не ту СК. ну и какую надо? чем полярка тут поможет? Давай вопрос ребром. ОК? :angry:
п314159> конечно не понял. Потому что оператор О. а М - некая пропорциональность в виде числа
Я о чём и говорю. Понять такие вещи ты просто не мог.
Пустынский, не строй из себя дурака. Ты еще недавно вообще не подозревал, что ошибку пишут через степень шага. Теперь ты начинаешь мол O(H4) ты теперь понял, а буквы Mh4 искал в Гугле?
 Ну ведь если бы ты хоть раз видел в жизни это выражение, ты бы так не кудахтал от удивления.
Ну ведь если бы ты хоть раз видел в жизни это выражение, ты бы так не кудахтал от удивления.Называется индюк думал и в суп попал

Изволь теперь представить строгое доказательство, а не байки о криворуком вычислителе.
в начале ты представишь строгое доказательство, что метод Адамса четвертого порядка (ты его записать хоть сможешь?) дает погрешность O(h4) или Mh4 (Ah4, Bh4, Kh4 ...
 ) а я уж потом подумаю
) а я уж потом подумаю 
п314159
втянувшийся
Красильников -
во времена примитивных БЦВМ главной проблемой была не точность счета, а объем вычислений и время. вот для такой "эффективности" таки да. Даже специально системы единиц можно выбирать/устанавливать. Где можно заменять плавайющие на целые или дроби целых - выигрыш в скорости.
чепуха. при оотказе БЦВМ идет закрутка. Куда там в пень мониторить при 10g ?
 вы соображать толком не можете, не то что управлять
вы соображать толком не можете, не то что управлять 
а точность выдачи импульса руками???
 в Землю попасть можно. В коридор трудно
в Землю попасть можно. В коридор трудно 
The choice of the coordinate system is of major importance because it will influence the effectiveness of the simulation tool.
во времена примитивных БЦВМ главной проблемой была не точность счета, а объем вычислений и время. вот для такой "эффективности" таки да. Даже специально системы единиц можно выбирать/устанавливать. Где можно заменять плавайющие на целые или дроби целых - выигрыш в скорости.
При спуске тоже можно было обойтись и без компьютера в случае его отказа. На "Аполлонах" имелась независимая система мониторинга входа, которая показывала текущие параметры полета и позволяла управлять спуском вручную, основываясь на ее показаниях.
чепуха. при оотказе БЦВМ идет закрутка. Куда там в пень мониторить при 10g ?

 вы соображать толком не можете, не то что управлять
вы соображать толком не можете, не то что управлять 
Вход в коридор обеспечивается заранее - путем соответствующих коррекций траектории. Компьютер на борту для этого не особо нужен - можно обойтись и наземным.
а точность выдачи импульса руками???

 в Землю попасть можно. В коридор трудно
в Землю попасть можно. В коридор трудно 
п314159> Красильников -
п314159>
п314159> во времена примитивных БЦВМ главной проблемой была не точность счета, а объем вычислений и время.
Статья-то написана в 2000 г. Это, конечно, время расцвета примитивных БЦВМ Они там еще к GPS привязываются
Они там еще к GPS привязываются 
п314159>
п314159> чепуха. при оотказе БЦВМ идет закрутка. Куда там в пень мониторить при 10g ?
 вы соображать толком не можете, не то что управлять
вы соображать толком не можете, не то что управлять 
Чепуха - это ваши "дифурки", которые дают 10 g Реально-то 4, с кратковременным возрастанием до 6...
Реально-то 4, с кратковременным возрастанием до 6...
И мониторить там было просто:
Смотри себе на два огонька - "вверх" и "вниз". Какой горит, туда и поворачивай вектор подъемной силы...
п314159>
п314159> а точность выдачи импульса руками???

Ну и с какой точностью можно руками выдать импульс в 21 секунду?
п314159>
The choice of the coordinate system is of major importance because it will influence the effectiveness of the simulation tool.
п314159> во времена примитивных БЦВМ главной проблемой была не точность счета, а объем вычислений и время.
Статья-то написана в 2000 г. Это, конечно, время расцвета примитивных БЦВМ
 Они там еще к GPS привязываются
Они там еще к GPS привязываются 
п314159>
При спуске тоже можно было обойтись и без компьютера в случае его отказа. На "Аполлонах" имелась независимая система мониторинга входа, которая показывала текущие параметры полета и позволяла управлять спуском вручную, основываясь на ее показаниях.
п314159> чепуха. при оотказе БЦВМ идет закрутка. Куда там в пень мониторить при 10g ?

 вы соображать толком не можете, не то что управлять
вы соображать толком не можете, не то что управлять 
Чепуха - это ваши "дифурки", которые дают 10 g
 Реально-то 4, с кратковременным возрастанием до 6...
Реально-то 4, с кратковременным возрастанием до 6...И мониторить там было просто:
The RSI shows the desired lift vector (up or down) by two lights, and a pointer that displays the current lift vector, which is used to confirm it is within the entry corridor.
Смотри себе на два огонька - "вверх" и "вниз". Какой горит, туда и поворачивай вектор подъемной силы...
п314159>
Вход в коридор обеспечивается заранее - путем соответствующих коррекций траектории. Компьютер на борту для этого не особо нужен - можно обойтись и наземным.
п314159> а точность выдачи импульса руками???


291:58:00 Scott: Okay, Houston; 15 with the burn status report.
291:58:02 Parker: Roger that.
291:58:04 Scott: Okay, Tig was on time. Burn time was 21 and came right out on the money, and it clicked up a couple of seconds after the shutdown to minus .1, 0 and minus .1. Delta-Vc was plus .8.
Ну и с какой точностью можно руками выдать импульс в 21 секунду?

Это сообщение редактировалось 12.09.2005 в 16:48
Красильников> Чепуха - это ваши "дифурки", которые дают 10 g Реально-то 4, с кратковременным возрастанием до 6...
Реально Вы не знаете. У Прохожего его дифуры, а у Вас голые слова НАСА.
Впрочем, там вполне могло быть именно 4 g, с кратковременным возрастанием до 6, если учесть, что вход был не на 11 км в сек, а на 9 км в сек
Реально Вы не знаете. У Прохожего его дифуры, а у Вас голые слова НАСА.
Впрочем, там вполне могло быть именно 4 g, с кратковременным возрастанием до 6, если учесть, что вход был не на 11 км в сек, а на 9 км в сек
291:58:00 Scott: Okay, Houston; 15 with the burn status report.
291:58:02 Parker: Roger that.
291:58:04 Scott: Okay, Tig was on time. Burn time was 21 and came right out on the money, and it clicked up a couple of seconds after the shutdown to minus .1, 0 and minus .1. Delta-Vc was plus .8.
Ваша ссылка - ДОКАЗАТЕЛЬСТВО, что вход А-15 был не на второй космической, а как обычный орбитальный полет
Красильников>> Чепуха - это ваши "дифурки", которые дают 10 g Реально-то 4, с кратковременным возрастанием до 6...
аФон+> Реально Вы не знаете. У Прохожего его дифуры, а у Вас голые слова НАСА.
У прохожего не дифуры, а именно "дифурки". В которых взятя средняя подъемная сила и начисто отсутствует управление оной в ходе спуска
и начисто отсутствует управление оной в ходе спуска 
А "голые слова НАСА" пока возражений у специалистов не вызывали...
аФон+> Впрочем, там вполне могло быть именно 4 g, с кратковременным возрастанием до 6, если учесть, что вход был не на 11 км в сек, а на 9 км в сек
А почему на 9, а не на 6?
аФон+> Реально Вы не знаете. У Прохожего его дифуры, а у Вас голые слова НАСА.
У прохожего не дифуры, а именно "дифурки". В которых взятя средняя подъемная сила
 и начисто отсутствует управление оной в ходе спуска
и начисто отсутствует управление оной в ходе спуска 
А "голые слова НАСА" пока возражений у специалистов не вызывали...
аФон+> Впрочем, там вполне могло быть именно 4 g, с кратковременным возрастанием до 6, если учесть, что вход был не на 11 км в сек, а на 9 км в сек
А почему на 9, а не на 6?

аФон+>
аФон+> Ваша ссылка - ДОКАЗАТЕЛЬСТВО, что вход А-15 был не на второй космической, а как обычный орбитальный полет [»]




291:58:00 Scott: Okay, Houston; 15 with the burn status report.
аФон+> 291:58:02 Parker: Roger that.
аФон+> 291:58:04 Scott: Okay, Tig was on time. Burn time was 21 and came right out on the money, and it clicked up a couple of seconds after the shutdown to minus .1, 0 and minus .1. Delta-Vc was plus .8.
аФон+> Ваша ссылка - ДОКАЗАТЕЛЬСТВО, что вход А-15 был не на второй космической, а как обычный орбитальный полет [»]




Y.K.> У прохожего не дифуры, а именно "дифурки". В которых взятя средняя подъемная сила  и начисто отсутствует управление оной в ходе спуска
и начисто отсутствует управление оной в ходе спуска
Ничего в этом страшного нет, как оценка годится, поскольку дает близкие значения к Зондам , к А-7 и А-9.
Y.K.> А почему на 9, а не на 6? [»]
[»]
11-6=5 км в сек хар. скорости погасить на Аполлоне было нечем, а вот 2 км в сек было чем (если не переходишь на орбиту ИСЛ, то приземляешься, как белый человек ничего не боясь)
 и начисто отсутствует управление оной в ходе спуска
и начисто отсутствует управление оной в ходе спуска Ничего в этом страшного нет, как оценка годится, поскольку дает близкие значения к Зондам , к А-7 и А-9.
Y.K.> А почему на 9, а не на 6?
 [»]
[»]11-6=5 км в сек хар. скорости погасить на Аполлоне было нечем, а вот 2 км в сек было чем (если не переходишь на орбиту ИСЛ, то приземляешься, как белый человек ничего не боясь)
Это сообщение редактировалось 12.09.2005 в 17:11
Y.K.>> У прохожего не дифуры, а именно "дифурки". В которых взятя средняя подъемная сила  и начисто отсутствует управление оной в ходе спуска
и начисто отсутствует управление оной в ходе спуска
аФон+> Ничего в этом страшного нет, как оценка годится, поскольку дает близкие значения к Зондам , к А-7 и А-9.
А при чем тут Зонды, А-7 и А-9?
 и начисто отсутствует управление оной в ходе спуска
и начисто отсутствует управление оной в ходе спуска аФон+> Ничего в этом страшного нет, как оценка годится, поскольку дает близкие значения к Зондам , к А-7 и А-9.
А при чем тут Зонды, А-7 и А-9?

п314159
втянувшийся
Смотри себе на два огонька - "вверх" и "вниз". Какой горит, туда и поворачивай вектор подъемной силы...
я конечно дико извиняюсь, а кто этот таинственный, который говорит на что жать???
 если у вас компутер дает подсказки - ну он еще лучше может и на кнопки жать
если у вас компутер дает подсказки - ну он еще лучше может и на кнопки жать  Реле там поставить в цепи питания лампочек, что ли
Реле там поставить в цепи питания лампочек, что ли 
Космонавт нафига? мы говорим, что если компутер висит с вашей елочной гирляндой, или огни горят по барабану - тогда что?

Чепуха - это ваши "дифурки", которые дают 10 g Реально-то 4, с кратковременным возрастанием до 6...
напишите ваши "дифурки", покажите мне 6

А "голые слова НАСА" пока возражений у специалистов не вызывали...
у кого именно не вызвали - список огласите? я имею ввиду тех кто с этим вопросом разбирался. Шунейко не вспоминать - там подлог рисунка.

При том, что они тестовые для модели (по ним данные есть, а по А-8, А10-А17 данные намерено искажены)
скажу больше - по А17 данные носят накидочный характер со слов НАСА. Даже в НАСА их толком не знают

цитата:
[2]Some Apollo 17 entry phase data are preflight predictions because actual data were not obtained.
Entry
п314159>
п314159> я конечно дико извиняюсь, а кто этот таинственный, который говорит на что жать??? если у вас компутер дает подсказки - ну он еще лучше может и на кнопки жать
если у вас компутер дает подсказки - ну он еще лучше может и на кнопки жать  Реле там поставить в цепи питания лампочек, что ли
Реле там поставить в цепи питания лампочек, что ли 
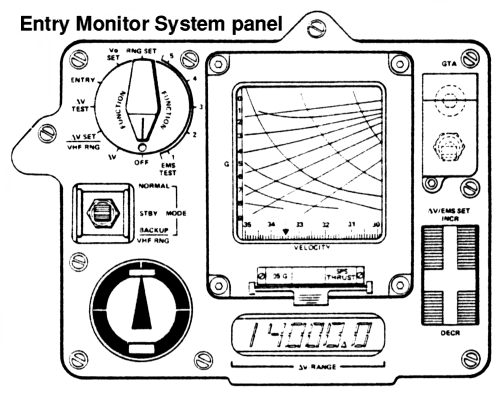
Никакой таинственности - на что жать, говорит EMS, т.е. Entry Monitor System.
п314159> Космонавт нафига? мы говорим, что если компутер висит с вашей елочной гирляндой, или огни горят по барабану - тогда что?
Мы говорим, что если компьютер висит, то EMS (независимая от него система) скорее всего работает и дает пилоту информацию, куда рулить вектором подъемной силы - вверх или вниз.
п314159>
п314159> напишите ваши "дифурки", покажите мне 6
Да они давно написаны. Айзеком Ньютоном - слышали про такого? Подставьте в них алгоритм управления подъемной силой вместо "средней температуры по больнице"
Подставьте в них алгоритм управления подъемной силой вместо "средней температуры по больнице"  Думаю, все сойдется
Думаю, все сойдется 
п314159>
п314159> у кого именно не вызвали - список огласите? я имею ввиду тех кто с этим вопросом разбирался. Шунейко не вспоминать - там подлог рисунка
Да нет, это вы список огласите - список тех, у кого возражения. Себя не предлагать
Смотри себе на два огонька - "вверх" и "вниз". Какой горит, туда и поворачивай вектор подъемной силы...
п314159> я конечно дико извиняюсь, а кто этот таинственный, который говорит на что жать???
 если у вас компутер дает подсказки - ну он еще лучше может и на кнопки жать
если у вас компутер дает подсказки - ну он еще лучше может и на кнопки жать  Реле там поставить в цепи питания лампочек, что ли
Реле там поставить в цепи питания лампочек, что ли 
Никакой таинственности - на что жать, говорит EMS, т.е. Entry Monitor System.
The EMS is not a single display, rather, it is a specialized guidance and display system to present critical entry parameters to the crew. Surprisingly, the EMS does not generate guidance or trajectory information for the spacecraft computer, nor can it actively control the spacecraft during entry. Its function is only to display the most relevant data to the crew as they plunge through the atmosphere. Three displays on the EMS provide the situational data necessary to evaluate the progress of the entry: A scrolling display showing velocity vs. deceleration, the RSI (Roll Stability Indicator), and a digital velocity indicator.
Most attention is focused on the velocity vs. deceleration display, a 9-cm window behind which is a scrolling Mylar tape marked with the acceptable velocity and G-force boundaries. The tape moves from right to left, and an illuminated index, or "bug", traces the current velocity-acceleration profile onto it. Of course, keeping the Command Module within the narrow entry corridor requires maneuverability within the atmosphere. A modest amount of lift is generated by the Command Module which can be vectored in any direction by rolling the spacecraft. The RSI shows the desired lift vector (up or down) by two lights, and a pointer that displays the current lift vector, which is used to confirm it is within the entry corridor. Finally, a digital velocity meter provides an additional source of velocity data to the crew.
п314159> Космонавт нафига? мы говорим, что если компутер висит с вашей елочной гирляндой, или огни горят по барабану - тогда что?
Мы говорим, что если компьютер висит, то EMS (независимая от него система) скорее всего работает и дает пилоту информацию, куда рулить вектором подъемной силы - вверх или вниз.
п314159>
Чепуха - это ваши "дифурки", которые дают 10 g Реально-то 4, с кратковременным возрастанием до 6...
п314159> напишите ваши "дифурки", покажите мне 6

Да они давно написаны. Айзеком Ньютоном - слышали про такого?
 Подставьте в них алгоритм управления подъемной силой вместо "средней температуры по больнице"
Подставьте в них алгоритм управления подъемной силой вместо "средней температуры по больнице"  Думаю, все сойдется
Думаю, все сойдется 
п314159>
А "голые слова НАСА" пока возражений у специалистов не вызывали...
п314159> у кого именно не вызвали - список огласите? я имею ввиду тех кто с этим вопросом разбирался. Шунейко не вспоминать - там подлог рисунка
Да нет, это вы список огласите - список тех, у кого возражения. Себя не предлагать

п314159
втянувшийся
аФон -
попробуйте поискать такую штуку как перигей траектории спуска Аполлонов.
Найдете - дайте знать. Хочу сравнить с угловыми данными входа - а то у меня есть сомнения...
попробуйте поискать такую штуку как перигей траектории спуска Аполлонов.
Найдете - дайте знать. Хочу сравнить с угловыми данными входа - а то у меня есть сомнения...
п314159
втянувшийся
Никакой таинственности - на что жать, говорит EMS, т.е. Entry Monitor System.
это фамилиё такое??? если это ДРУГОЙ компутер, то мы вернулись к вопросам надежности, дублировнаия БЦВМ и пр. Если света нет - твой речевой информатор работать будет? или КЗ к примеру?
п314159
втянувшийся
п314159> напишите ваши "дифурки", покажите мне 6
Да они давно написаны. Айзеком Ньютоном - слышали про такого?
ага. в редакции Айзика Азимова

п314159>
п314159> это фамилиё такое??? если это ДРУГОЙ компутер, то мы вернулись к вопросам надежности, дублировнаия БЦВМ и пр. Если света нет - твой речевой информатор работать будет? или КЗ к примеру? [»]
Это не "другой компьютер", а аналоговая система на базе акселерометра, гироскопов и т.п. простых приборов. Такое не зависает. А если и сломается, то это уже из совсем другой оперы. К тому же часть данных идет (и дублируется) с Земли. Так было и на наших Зондах, не помню который там упал из-за того, что с Евпатории передали неправильную команду на коррекцию траектории паред входом.
Никакой таинственности - на что жать, говорит EMS, т.е. Entry Monitor System.
п314159>
п314159> это фамилиё такое??? если это ДРУГОЙ компутер, то мы вернулись к вопросам надежности, дублировнаия БЦВМ и пр. Если света нет - твой речевой информатор работать будет? или КЗ к примеру? [»]
Это не "другой компьютер", а аналоговая система на базе акселерометра, гироскопов и т.п. простых приборов. Такое не зависает. А если и сломается, то это уже из совсем другой оперы. К тому же часть данных идет (и дублируется) с Земли. Так было и на наших Зондах, не помню который там упал из-за того, что с Евпатории передали неправильную команду на коррекцию траектории паред входом.
Y.K.> А вот что другие люди пишут на эту тему:
Y.K.> Это из "Atmospheric Reentry Modeling and Simulation" ( http://spacecraft.ssl.umd.edu/design_lib/JSRv39n4.entry_sim.pdf ) - статьи, специально посвященной численному моделированию процесса входа
Бросьте, Юрий. Ведь совершенно очевидно, что все эти люди - "просто невежды высшей пробы. ТОЧНОСТЬ решения задачи не может зависть от способа выбора координат. замена координат может помочь при бумажно-аналитическом способе решения. Численно - это до задницы".

 Прохожий - он точно знает. Он же крупный спец.
Прохожий - он точно знает. Он же крупный спец. 
The choice of the coordinate system is of major importance because it will influence the effectiveness of the simulation tool.
Y.K.> Это из "Atmospheric Reentry Modeling and Simulation" ( http://spacecraft.ssl.umd.edu/design_lib/JSRv39n4.entry_sim.pdf ) - статьи, специально посвященной численному моделированию процесса входа

Бросьте, Юрий. Ведь совершенно очевидно, что все эти люди - "просто невежды высшей пробы. ТОЧНОСТЬ решения задачи не может зависть от способа выбора координат. замена координат может помочь при бумажно-аналитическом способе решения. Численно - это до задницы".


 Прохожий - он точно знает. Он же крупный спец.
Прохожий - он точно знает. Он же крупный спец. 
п314159> Факир -
п314159>
п314159> процентов от чего??? Я вас уверяю, что разницы между полярными и декартовыми координатами никакой. Разница появляется там, где под "заменой" координат вы на самом деле сводите задачу к другой. То бишь вставляете кусок "физики" в "математику".
Я вас уверяю, что разницы между полярными и декартовыми координатами никакой. Разница появляется там, где под "заменой" координат вы на самом деле сводите задачу к другой. То бишь вставляете кусок "физики" в "математику".
Ну что ты продолжаешь бредить? Факир же тебе ясно написал, тут даже добавить нечего: "
Ты это прочёл? Но не понял? Разжёвываю: уравнения разного вида наиболее эффективно решаются разными методами. В разных координатах уравнения имеют разную форму, и потому эффективно решаются по-разному. В одних координатах уравнения могут иметь форму, не допускающую эффективного решения - а в других решение будет найдено быстро и просто.
В конце концов, если ты не можешь понять умом - поверь умным людям, которые специально занимаются моделированием того самого и ссылку на которых дал Юрий. Конечно, твоя заочная дискуссия с ними и объявление их невеждами по-своему любопытны, но это любопытство чисто медицинского свойства. Здесь поверят не тебе, а профессионалам, занимающимся моделированием процессов атмосферного торможения и утверждающим, что "The choice of the coordinate system is of major importance because it will influence the effectiveness of the simulation tool" - http://spacecraft.ssl.umd.edu/design_lib/JSRv39n4.entry_sim.pdf
Здесь поверят не тебе, а профессионалам, занимающимся моделированием процессов атмосферного торможения и утверждающим, что "The choice of the coordinate system is of major importance because it will influence the effectiveness of the simulation tool" - http://spacecraft.ssl.umd.edu/design_lib/JSRv39n4.entry_sim.pdf 
п314159> Ну чтоб вы поняли - это тоже самое, как утверждать, что в килограммах задача решается хуже, чем скажем в фунтах или пудах
Ты не представляешь, насколько ты прав. Ты представлял бы, если бы знал, что метрология - это не просто очередное красиво звучащее слово, а очень серьёзная дисциплина, и точность решения множества актуальных задач находится в теснейшей связи с выбором системы единиц измерения.
Ты представлял бы, если бы знал, что метрология - это не просто очередное красиво звучащее слово, а очень серьёзная дисциплина, и точность решения множества актуальных задач находится в теснейшей связи с выбором системы единиц измерения.  Но откуда ж тебе это знать, ты о метрологии и не слышал-то, небось, для тебя выбор системы единиц - лишь ни на что не влияющее формальное преобразование... Ты и представить себе не можешь, как обстоят дела в реальности.
Но откуда ж тебе это знать, ты о метрологии и не слышал-то, небось, для тебя выбор системы единиц - лишь ни на что не влияющее формальное преобразование... Ты и представить себе не можешь, как обстоят дела в реальности. 
п314159>
п314159> твое высокомерие тут не уместно. Он Пискунов, а ты никто. Пустынский. Так что помолчи.
Всё? Облажался, и ничего больше не осталось, как только отбрехиваться? Где ты тут высокомерие усмотрел? Я, вроде, нигде не выказывал никакого отношения к составителям школьных и инженерных справочников? К тебе, который увидал в инженерном справочнике упрощённую формулировку и решил, что это "общепринятая терминология математическая" - высазывал. Потому что ты ни ухом ни рылом в том, о чём пытаешься судить, и даже не трудишься хоть несколько минут уделить знакомству с предметом прежде, чем начать поучать других. Но это не высокомерие, а помощь тебе в самоистязании. Ты ж ради этого снова и снова нещадно подставляешься там, где спокойно мог бы держать язык за зубами?
Да, что там с методом Адамса? Решил замять? Не будешь доказывать свою брехню о расходимостях?
п314159>
п314159> Лично у меня было два уравнения второго порядка. И его решения - две функции Y=Y(t) X=X(t). Все остальное - промежуточные результаты. Куда дальше будем упрощать??? в полярных тоже будет две координаты. Мы говорим о конкретной задаче, а не вообще
Да шо ты гавариш? Ещё совсем недавно ты имел какие-то особые претензии к моим словам о том, что выбор СК в небесной механике очень важен. "для задач двух- и Н-тел разница между полярные/прямоугольные/хоть цилиндрические никакая. Количество уравнений от этого не меняется. Сколько степеней свободы - столько и решать" - вроде, так ты грил? Теперь решил замять?
Лана. Я тебе насчёт той самой задачи могу лишь ещё раз повторить: в полярных координатах запись исходных уравнений намного естественнее, чем в прямоугольных. Запись проще, решение потенциально будет проще и точнее.
п314159> Ты на меня наехал, мол я выбрал не ту СК. ну и какую надо? чем полярка тут поможет? Давай вопрос ребром. ОК?
Всё? По остальным пунктам капитуляция? Решил попоучать всех, а вышел облом, как всегда? Осталось только отступить на старые позиции и вернуться к тому, с чего начали? Похныкать - в чём, мол, ты маху дал?
Ещё раз, кратко. На значительной части траектории аэродинамические силы меньше или сравнимы с гравитационными (длина траектории - порядка 30 градусов на поверхности Земли), а посему задача является, фактически, небесно-механической с аэродинамическими возмущениями. Такие задачи в полярных координатах решаются в общем случае проще и естественнее.
п314159> Пустынский, не строй из себя дурака. Ты еще недавно вообще не подозревал, что ошибку пишут через степень шага. Теперь ты начинаешь мол O(H4) ты теперь понял, а буквы Mh4 искал в Гугле? Ну ведь если бы ты хоть раз видел в жизни это выражение, ты бы так не кудахтал от удивления.
Ну ведь если бы ты хоть раз видел в жизни это выражение, ты бы так не кудахтал от удивления.
п314159> Называется индюк думал и в суп попал
Продолжай, Прохожий, продолжай! Очень, очень смешно! Мне нравится, когда тебя так колбасит.
п314159>
п314159> в начале ты представишь строгое доказательство, что метод Адамса четвертого порядка (ты его записать хоть сможешь?) дает погрешность O(h4) или Mh4 (Ah4, Bh4, Kh4 ... ) а я уж потом подумаю
) а я уж потом подумаю 
Т. е. полная капитуляция, так? Ну а то, что ты просишь, ты легко найдёшь в соответствующем справочнике - а я тебе не справочник.
Ну а то, что ты просишь, ты легко найдёшь в соответствующем справочнике - а я тебе не справочник. 
п314159> во времена примитивных БЦВМ главной проблемой была не точность счета, а объем вычислений и время. вот для такой "эффективности" таки да. Даже специально системы единиц можно выбирать/устанавливать.
Ты будешь смеяться, но "объём вычислений и время" до сих пор остаётся главной проблемой. Причём везде, всегда и повсюду. Но откуда тебе это знать...
Причём везде, всегда и повсюду. Но откуда тебе это знать... 
п314159> Шунейко не вспоминать - там подлог рисунка.
Какого???
п314159> у кого именно не вызвали - список огласите? я имею ввиду тех кто с этим вопросом разбирался.
Ну вот Попов годится? http://epizodsspace.testpilot.ru/bibl/popov_sa/obl.html
Гэтланд? http://epizodsspace.testpilot.ru/bibl/getlend/obl.html
п314159>
Вероятно, при решении одной и той же задачи в полярных и декартовых, особенно при подобранной на скорую руку сетке, оно вполне может достигать и десятков процентов.
п314159> процентов от чего???
 Я вас уверяю, что разницы между полярными и декартовыми координатами никакой. Разница появляется там, где под "заменой" координат вы на самом деле сводите задачу к другой. То бишь вставляете кусок "физики" в "математику".
Я вас уверяю, что разницы между полярными и декартовыми координатами никакой. Разница появляется там, где под "заменой" координат вы на самом деле сводите задачу к другой. То бишь вставляете кусок "физики" в "математику".Ну что ты продолжаешь бредить? Факир же тебе ясно написал, тут даже добавить нечего: "
в разных системах координат исходные (аналитические) уравнения будут различаться
, иногда очень существенно, что, в свою очередь, приводит к различным методам их численного решения, различным сеткам
и т.п".Ты это прочёл? Но не понял? Разжёвываю: уравнения разного вида наиболее эффективно решаются разными методами. В разных координатах уравнения имеют разную форму, и потому эффективно решаются по-разному. В одних координатах уравнения могут иметь форму, не допускающую эффективного решения - а в других решение будет найдено быстро и просто.
В конце концов, если ты не можешь понять умом - поверь умным людям, которые специально занимаются моделированием того самого и ссылку на которых дал Юрий. Конечно, твоя заочная дискуссия с ними и объявление их невеждами по-своему любопытны, но это любопытство чисто медицинского свойства.
 Здесь поверят не тебе, а профессионалам, занимающимся моделированием процессов атмосферного торможения и утверждающим, что "The choice of the coordinate system is of major importance because it will influence the effectiveness of the simulation tool" - http://spacecraft.ssl.umd.edu/design_lib/JSRv39n4.entry_sim.pdf
Здесь поверят не тебе, а профессионалам, занимающимся моделированием процессов атмосферного торможения и утверждающим, что "The choice of the coordinate system is of major importance because it will influence the effectiveness of the simulation tool" - http://spacecraft.ssl.umd.edu/design_lib/JSRv39n4.entry_sim.pdf 
п314159> Ну чтоб вы поняли - это тоже самое, как утверждать, что в килограммах задача решается хуже, чем скажем в фунтах или пудах

Ты не представляешь, насколько ты прав.
 Ты представлял бы, если бы знал, что метрология - это не просто очередное красиво звучащее слово, а очень серьёзная дисциплина, и точность решения множества актуальных задач находится в теснейшей связи с выбором системы единиц измерения.
Ты представлял бы, если бы знал, что метрология - это не просто очередное красиво звучащее слово, а очень серьёзная дисциплина, и точность решения множества актуальных задач находится в теснейшей связи с выбором системы единиц измерения.  Но откуда ж тебе это знать, ты о метрологии и не слышал-то, небось, для тебя выбор системы единиц - лишь ни на что не влияющее формальное преобразование... Ты и представить себе не можешь, как обстоят дела в реальности.
Но откуда ж тебе это знать, ты о метрологии и не слышал-то, небось, для тебя выбор системы единиц - лишь ни на что не влияющее формальное преобразование... Ты и представить себе не можешь, как обстоят дела в реальности. 
п314159>
Я вообще-то этот справочник лишь изредка видел и едва ли открывал, но если он действительно для ВТУЗов, то мои слова "А запись через пропорцию встречается чаще в простых справочниках - школьных или инженерных" оказались верны с точностью до буквы.
п314159> твое высокомерие тут не уместно. Он Пискунов, а ты никто. Пустынский. Так что помолчи.

Всё? Облажался, и ничего больше не осталось, как только отбрехиваться? Где ты тут высокомерие усмотрел? Я, вроде, нигде не выказывал никакого отношения к составителям школьных и инженерных справочников? К тебе, который увидал в инженерном справочнике упрощённую формулировку и решил, что это "общепринятая терминология математическая" - высазывал. Потому что ты ни ухом ни рылом в том, о чём пытаешься судить, и даже не трудишься хоть несколько минут уделить знакомству с предметом прежде, чем начать поучать других. Но это не высокомерие, а помощь тебе в самоистязании. Ты ж ради этого снова и снова нещадно подставляешься там, где спокойно мог бы держать язык за зубами?
Да, что там с методом Адамса? Решил замять? Не будешь доказывать свою брехню о расходимостях?
п314159>
В задаче 2-х тел сколько степеней свободы? 6 было испокон веков. Ну так вот в произвольных прямоугольных координатах ИСО и будет 6 уравнений 2-го порядка. Простое преобразование координат "сдвиг-поворот" уменьшит число уравнений до 2-х уравнений 2-го порядка. А переход к координатам "обратный радиус-вектор - угол" оставит трансцендентное уравнение Кеплера да уравнение Бине
п314159> Лично у меня было два уравнения второго порядка. И его решения - две функции Y=Y(t) X=X(t). Все остальное - промежуточные результаты. Куда дальше будем упрощать??? в полярных тоже будет две координаты. Мы говорим о конкретной задаче, а не вообще

Да шо ты гавариш? Ещё совсем недавно ты имел какие-то особые претензии к моим словам о том, что выбор СК в небесной механике очень важен. "для задач двух- и Н-тел разница между полярные/прямоугольные/хоть цилиндрические никакая. Количество уравнений от этого не меняется. Сколько степеней свободы - столько и решать" - вроде, так ты грил? Теперь решил замять?
Лана. Я тебе насчёт той самой задачи могу лишь ещё раз повторить: в полярных координатах запись исходных уравнений намного естественнее, чем в прямоугольных. Запись проще, решение потенциально будет проще и точнее.
п314159> Ты на меня наехал, мол я выбрал не ту СК. ну и какую надо? чем полярка тут поможет? Давай вопрос ребром. ОК?
Всё? По остальным пунктам капитуляция? Решил попоучать всех, а вышел облом, как всегда? Осталось только отступить на старые позиции и вернуться к тому, с чего начали? Похныкать - в чём, мол, ты маху дал?
Ещё раз, кратко. На значительной части траектории аэродинамические силы меньше или сравнимы с гравитационными (длина траектории - порядка 30 градусов на поверхности Земли), а посему задача является, фактически, небесно-механической с аэродинамическими возмущениями. Такие задачи в полярных координатах решаются в общем случае проще и естественнее.
п314159>> конечно не понял. Потому что оператор О. а М - некая пропорциональность в виде числа
п314159> Я о чём и говорю. Понять такие вещи ты просто не мог.
п314159> Пустынский, не строй из себя дурака. Ты еще недавно вообще не подозревал, что ошибку пишут через степень шага. Теперь ты начинаешь мол O(H4) ты теперь понял, а буквы Mh4 искал в Гугле?
 Ну ведь если бы ты хоть раз видел в жизни это выражение, ты бы так не кудахтал от удивления.
Ну ведь если бы ты хоть раз видел в жизни это выражение, ты бы так не кудахтал от удивления.п314159> Называется индюк думал и в суп попал

Продолжай, Прохожий, продолжай! Очень, очень смешно! Мне нравится, когда тебя так колбасит.

п314159>
Изволь теперь представить строгое доказательство, а не байки о криворуком вычислителе.
п314159> в начале ты представишь строгое доказательство, что метод Адамса четвертого порядка (ты его записать хоть сможешь?) дает погрешность O(h4) или Mh4 (Ah4, Bh4, Kh4 ...
 ) а я уж потом подумаю
) а я уж потом подумаю 
Т. е. полная капитуляция, так?
 Ну а то, что ты просишь, ты легко найдёшь в соответствующем справочнике - а я тебе не справочник.
Ну а то, что ты просишь, ты легко найдёшь в соответствующем справочнике - а я тебе не справочник. 
п314159> во времена примитивных БЦВМ главной проблемой была не точность счета, а объем вычислений и время. вот для такой "эффективности" таки да. Даже специально системы единиц можно выбирать/устанавливать.
Ты будешь смеяться, но "объём вычислений и время" до сих пор остаётся главной проблемой.
 Причём везде, всегда и повсюду. Но откуда тебе это знать...
Причём везде, всегда и повсюду. Но откуда тебе это знать... 
п314159> Шунейко не вспоминать - там подлог рисунка.
Какого???

п314159> у кого именно не вызвали - список огласите? я имею ввиду тех кто с этим вопросом разбирался.
Ну вот Попов годится? http://epizodsspace.testpilot.ru/bibl/popov_sa/obl.html
Гэтланд? http://epizodsspace.testpilot.ru/bibl/getlend/obl.html
Это сообщение редактировалось 13.09.2005 в 00:43
п314159
втянувшийся
Разжёвываю: уравнения разного вида наиболее эффективно решаются разными методами. В разных координатах уравнения имеют разную форму, и потому эффективно решаются по-разному. В одних координатах уравнения могут иметь форму, не допускающую эффективного решения - а в других решение будет найдено быстро и просто.
общие слова. масло маслянное

В конце концов, если ты не можешь понять умом - поверь умным людям, которые специально занимаются моделированием того самого и ссылку на которых дал Юрий
так меня уже пытались такой туфтой разоблачить - я даже поместил результаты той другой модели, которую дал Красильников. Там результаты для Аполло еще хуже
 в итоге дело замяли...
в итоге дело замяли... 
Всё? Облажался, и ничего больше не осталось, как только отбрехиваться? Где ты тут высокомерие усмотрел? Я, вроде, нигде не выказывал никакого отношения к составителям школьных и инженерных справочников?
вот потому что ты курс дифференциального и интегрального исчисления Пискунова обозвал "справочником" - закрой рот :angry:
Да, что там с методом Адамса? Решил замять? Не будешь доказывать свою брехню о расходимостях?
кому - тебе что ли?

п314159> Ты на меня наехал, мол я выбрал не ту СК. ну и какую надо? чем полярка тут поможет? Давай вопрос ребром. ОК?
Ещё раз, кратко. На значительной части траектории аэродинамические силы меньше или сравнимы с гравитационными (длина траектории - порядка 30 градусов на поверхности Земли), а посему задача является, фактически, небесно-механической с аэродинамическими возмущениями. Такие задачи в полярных координатах решаются в общем случае проще и естественнее.
Так. Пустынскому был задан вопрос в лоб - у меня два уравнения второго порядка в прямоугольной системе. Нафига менять шило на мыло? И что он ответил?


Иначе как ерундой твои советы назвать сложно.
Понимаешь - все что ты говоришь - звуки пустой погремушки

У Сихарулидзе уравнения пишутся в нормально-человеческой декартовой системе координат. А ты умный, да?
К тому же в полярной системе аэродинамические силы будут выглядеть весьма криво

У тебя был простой путь - показать вот система Прохожего, вот так ее можно показать в такой-то системе координат. Все видят - да проще. Или нифига - теже яйца...
Граждане! я задал Пустынскому аж один вопрос ребром - как и на что можно заменить с целью упрощения два уравнения второго порядка в координатах ХУ. И что он мне ответил?
Вот что: Всё? По остальным пунктам капитуляция? Решил попоучать всех, а вышел облом, как всегда? Осталось только отступить на старые позиции и вернуться к тому, с чего начали? Похныкать - в чём, мол, ты маху дал?
Да. Ильф и Петров. Шахматный матч в Васюках



п314159
втянувшийся
Короче, вот система:
x″ = –Q*(vx/v) –Pу*(vy/v) –(μ/r²)*x/r
y″ = –Q*(vy/v) +Pу*(vx/v) –(μ/r²)*y/r
здесь
x′ = vx
y′ = vy
v² = vx² + vy²
r² = x² + y²
h = r – r0
Q=Cx*S*ρ(h)*v² /2m
Pу=cos(γ)*Cy*S*ρ(h)*v² /2m
Пустынский! у тебя есть шанс - запиши систему в полярных координатах и мы увидем - станет от этого проще или нет. ОК?
или струсишь как всегда!?
x″ = –Q*(vx/v) –Pу*(vy/v) –(μ/r²)*x/r
y″ = –Q*(vy/v) +Pу*(vx/v) –(μ/r²)*y/r
здесь
x′ = vx
y′ = vy
v² = vx² + vy²
r² = x² + y²
h = r – r0
Q=Cx*S*ρ(h)*v² /2m
Pу=cos(γ)*Cy*S*ρ(h)*v² /2m
Пустынский! у тебя есть шанс - запиши систему в полярных координатах и мы увидем - станет от этого проще или нет. ОК?
или струсишь как всегда!?

Copyright © Balancer 1997..2021
Создано 29.04.2005
Связь с владельцами и администрацией сайта: anonisimov@gmail.com, rwasp1957@yandex.ru и admin@balancer.ru.
Создано 29.04.2005
Связь с владельцами и администрацией сайта: anonisimov@gmail.com, rwasp1957@yandex.ru и admin@balancer.ru.
 7-40
7-40

 инфо
инфо инструменты
инструменты аФон+
аФон+


 п314159
п314159

