Использование микроэлектромеханических (MEMS) акселерометров в ракетомоделях

pinko> Но если ракета летит по параболической траектории (с самого начала полета, или просто близко к апогеем)

pinko, ты все очень подробно и доходчиво описал , но это я прекрасно понимаю. Я не понимаю постановку вопроса. Весь сыр-бор с гироскопами-акселерометрами изначально возник для управления ракетой. Поэтому 1D здесь рассматривать вообще нет смысла. А вот задача 3D управления тоже может быть поставлена по-разному. Эта постановка зависит от того, что мы хотим. Вывести ракету на орбиту - это одно, достичь максимальной высоты ~ 100 км - это другое, а достичь высоты ~30км - это вообще третье. У меня складывается впечатление, что у всех участников дискуссии задачи разные, и это они не учитывают. А местами даже похоже не до конца сформулировали для себя способы решения.

pinko> Период 5:
pinko> - вычислено ускорение ракеты: -1,2ж
pinko> - реальное ускорение ракеты: -0,2ж
pinko> Обсуждение до сих пор было об этой ошибке, ее влияние на данных из датчиков БРЭО, как рассчитать данные от 1D и 3D датчиков и так далее.

Для того, чтобы подобная погрешность могла критично сказаться на точности определения апогея 1D акселерометром нужно, чтобы тяговооруженность ракеты была менее 4, а время работы двигателя не более 1с. Причём критично это становится на углах отклонения от вертикали более 40гр. Это примерно получается, что масса топлива для карамельного двигателя в такой ракете должна быть не более 4% от стартовой массы.
При этом высоты полёта такой ракеты получаются настолько низкими ~20-40м, что применение парашютной системы спасения оказывается вообще весьма сомнительно. Тут в принципе можно и не спасать вовсе.

В тоже время для обычных ракет и мощных высотных работает безупречно, даже на углах отклонения от вертикали до 70гр. А при нормальных углах отклонения в пределах 10-20гр. срабатывает ещё точнее и лучше, чем на барометрическом датчике.

Это всё я пишу применительно уже к своему алгоритму, который и начал тестировать в симуляторе.
Чуть позже будут и графики и даже виде процесса спасения в 3D.

SashaMaks> При этом высоты полёта такой ракеты получаются настолько низкими ~20-40м, что применение парашютной системы спасения оказывается вообще весьма сомнительно.

На барометрическом датчике такие высоты тоже были в недоступном пределе. Там этому порывы ветра мешали на старте. Поэтому недостатков перед барометрическим датчиком у 1D акселерометра нет, только преимущества.

RocKI> Я не понимаю постановку вопроса. ... У меня складывается впечатление, что у всех участников дискуссии задачи разные, и это они не учитывают. А местами даже похоже не до конца сформулировали для себя способы решения.

Ага, вот ответ - SashaMaks поделил своей идеей об определении апогея, или точнее активации системы спасение на минимальной скорости, в стандартного любительского полета с помощью акселерометры в самодельных БРЭО.

Это метод имеет определенные преимущества по сравнению с барометрического датчика - нет влияния местного давления, иммунных к эффектов сверхзвуковой скорости, нет 10-12 км предела высоты как барометрического датчика. Он имеет недостаток - близко к апогею, ракеты больше не вертикально - так это влияет на алгоритм принятия решений.

Несмотря на этот недостаток, как -VMK- отметил, "Aerocon G-Wiz" определяет апогей по данны от акселерометъра - так, очевидно, это метод уже был реализован и Aerocon G-Wiz и имеет много успешных стартов в США и остальной мир. Учитывая все преимущества и недостатки моя цель, чтобы исследовать этот метод и разработать надежный алгоритм. Думаю что, ето тоже цель Саши.

Pinko

pinko> Это метод имеет определенные преимущества по сравнению с барометрического датчика - нет влияния местного давления, иммунных к эффектов сверхзвуковой скорости, нет 10-12 км предела высоты как барометрического датчика. Он имеет недостаток - близко к апогею, ракеты больше не вертикально - так это влияет на алгоритм принятия решений.

Правильно, это задача для неуправляемой ракеты на высотах ~ 30 км, где важно просто поймать апогей. Т.е. управление ракетой вообще не при чем. Если смотреть полет на высоты близкие к 100 км, то там определение апогея не так актуально, зато важно выдержать вертикаль, т.е. возникает задача управления. Причем именно в постановке компенсации отклонений хотя бы на первой стадии полета, и можно аэродинамикой.

RocKI> Правильно, это задача для неуправляемой ракеты на высотах ~ 30 км, где важно просто поймать апогей.

1D акселерометр может работать на высотах до 100км и даже больше. Задача выдерживания вертикали для неуправляемой ракеты всё та же и всё там же - на активном участке полёта, а он много меньше 100км и проходит в плотной атмосфере. Если из плотной атмосферы уже вылетел по вертикали, в сильном разрежении, а уж тем более в вакууме, с выключенным двигателем, ничто уже не отклонит ракету.

И ракете вовсе не обязательно всё время лететь носом по ветру, чтобы сработал 1D акселерометр.

SashaMaks> Чуть позже будут и графики и даже виде процесса спасения в 3D.

У меня в модели, моделирование движения тел в пространстве идёт, как и всегда, и никак не связано с моделированием данных с датчиков.

Учитываются все силы, действующие на объект всегда, и получается инерционное ускорение центра масс тела. Вот его-то я отдельно и анализирую, уже когда весь процесс моделирования движения для тел в текущий момент времени полностью выполнен.

Поскольку векторы инерционной силы и инерционного ускорения сонаправлены, то убрать влияние силы тяжести можно на уровне ускорений. Так проще, чтобы не пересчитывать всю динамику заново, а условия связи между датчиком и корпусом тела позволяют это сделать.

GLRocket.A := SummABC(GLRocket.A, Sim_G);

В данном случае применена функция суммирования, после которой с учётом знаков из общего ускорения полностью выводится влияние силы гравитации на датчик в пространстве где бы он не находился и как бы он повёрнут не был.

После этого выполняется моделирование сигнала на осях акселерометра, делается это с помощью разложения полученного вектора ускорения A на вектора осей датчика X,Y,Z, которые совпадают с осями тела и пока что датчик находится в ЦМ тела:

Axel_A.X := ProekciaVectorAB(GLRocket.A, GLRocket.Coord.nX) + (Random(200) - 100) * 0.01;
Axel_A.Y := ProekciaVectorAB(GLRocket.A, GLRocket.Coord.nY) + (Random(200) - 100) * 0.01;
Axel_A.Z := ProekciaVectorAB(GLRocket.A, GLRocket.Coord.nZ) + (Random(200) - 100) * 0.01;

При этом в расчёте уже участвует совсем другая переменная Axel_A, а не GLRocket и они нигде не пересекаются и друг на друга не влияют. Плюс сразу же идёт моделирование шума в 200мG на каждую ось + (Random(200) - 100) * 0.01.

Далее, как я уже писал, просто идёт обработка данных с датчика отдельным алгоритмом и конкретно для 1D акселерометра, где я просто вычитаю g из исходных данных:

Axel_A.Y := Axel_A.Y - FGravitySI;

Таким образом мы устраняем недостаток g в показаниях с датчика.
После этого идёт простое суммирования прямо в полученных попугаях:

Axel := Axel + Axel_A.Y;

И наконец сам алгоритм выброса парашюта:

If (GL_Time > 1.0) and (Axel < 0.0) then GL_PAR := True;

Проще некуда.
Условие (Axel < 0.0) – главное для определения момента выброса парашюта.
Условие (GL_Time > 1.0) – дополнительное и в данном случае сильно упрощенное и вообще временное, так как тут определяется фаза старта ракеты и даётся добро на запуск алгоритма суммирования ускорений, но в симуляторе это усложнение ни к чему, а сам алгоритм для МК уже есть ещё на примере работы барометрического датчика.

После того, как сумма ускорений уйдёт в ноль, переменная GL_PAR активизирует алгоритм моделирования системы спасения в симуляторе. При этом всё, что происходит – это изменяется Cx и Sx для тела в виде парашюта и больше ничего. Всё остальное, что получается (резко тормозится тело ракеты и начинает падать вертикально в низ), происходит в результате работы матмодели.

Ракета:
Масса 5,45кг
УИ 120с.
Тяга 1000Н
Время тяги 1с.
Cx 0,4
Sx 0,00385м²
Углы старта: 20гр., 40гр., 60гр., 70гр.

3D модель ракеты по размерам условна.

Ракета:
Масса 5,0968399кг
УИ 120с.
Тяга 150Н
Время тяги 1с.
Cx 0,4
Sx 0,00385м²
Углы старта: 0гр., 10гр., 20гр., 30гр., 35гр., 40гр., 45гр., 50гр.

Тяговооруженность всего лишь 3 и то до 45гр. вполне нормально всё сработало.

Хорошо бы на графиках показать время принятия решения выпуска парашюта.

I.C.> Хорошо бы на графиках показать время принятия решения выпуска парашюта.

У ракеты есть характеристическая скорость.
Это та скорость, которую ракета набрала бы в невесомости и без сопротивления воздуха.
Если ракета летит вертикально вверх, то время её полёта до верхней точки, когда скорость станет равна нулю, считается по примитивной школьной формуле:

t = v0 / g

где v0 — характеристическая скорость, g = 9.81 — гравитация.

Если заранее знать характеристическую скорость, то момент достижения ракетой верхней точки можно было бы определять по предустановленному таймеру. Без всяких гироскопов.

Однако, эта скорость заранее неизвестна.
Но если поставить акселерометр и интегрировать его показания, то в момент окончания работы двигателя наинтегрированная скорость как раз и будет фактической характеристической скоростью.
А если из показаний акселерометра постоянно вычитать g и только потом интегрировать, то как раз через время t = v0 / g наинтегрированная скорость станет равной нулю.

Другие случаи.

Если ракета стартует криво и летит под углом.
Время t = v0 / g при этом остаётся тем же самым, но вертикальная составляющая скорости оказывается меньше.
Это значит, что ракета успеет достичь апогея и начнёт снижаться, и только потом настанет момент времени t — сработает после апогея.

Если есть сопротивление воздуха (вертикальный полёт).
Оно уменьшает ускорение, создаваемое двигателем, так что в момент окончания работы двигателя скорость наинтегрируется меньше характеристической.
И потом торможение от сопротивления будет эту скорость уменьшать быстрее, так что время кончится раньше, чем без сопротивления воздуха.
Но при вертикальном полёте при этом будет достигнута именно точка апогея, когда скорость равна нулю.

Если под углом и сопротивление воздуха.
По результатам симуляции — сопротивление пододвигает опаздывающий момент срабатывания ближе к апогею.
И чем оно больше, тем ближе. (При неразумно большом — даже раньше апогея.)

Простого и всем понятного объяснения этого у меня нет.

Xan> У ракеты есть характеристическая скорость...

Xan, спасибо за отличную резюме нашей дискуссии до сих пор!

pinko> Но если ракета летит по параболической траектории (с самого начала полета, или просто близко к апогеем), как упоминалось ранее - мы делаем коррекции с 1ж, однако мы были должны сделать исправлены с менее чем 1ж потому что гравитационной компонент меняется - это вызывает ошибку.

Утверждение вида: "это вызывает ошибку" важно проверить количественно, но этого не было сделано, а вывод прозвучал.

Неучтённые факты:
1. Стартовый угол ракет от вертикали обычно не превышает 10-20гр.
2. Векторная сумма всех сил относительно локальной системы отсчёта.
3. Многократная разница между модулями векторов силы тяги и силы тяжести.
4. Распределение ускорений по длине траектории с учётом её кривизны.
5. Влияние изменения относительного угла поворота результирующего вектора на итоговую сумму и её погрешность.
6. Накопление ошибки всей суммы по всей длине траектории - интеграла ускорений.

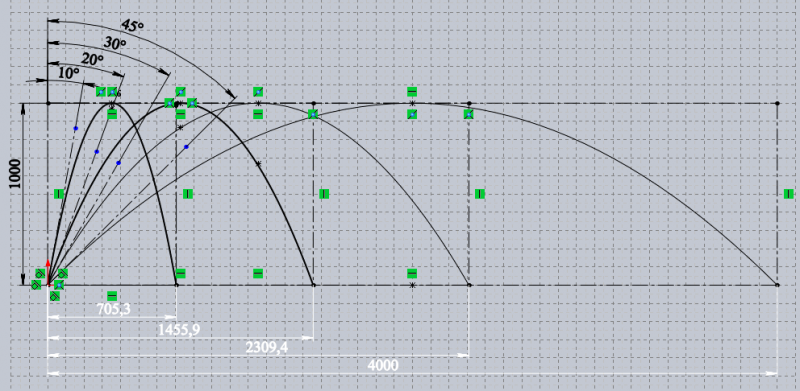
SashaMaks> 1. Стартовый угол ракет от вертикали обычно не превышает 10-20гр.

Нарисовал наглядно на примере параболы:

SashaMaks> Утверждение вида: "это вызывает ошибку" важно проверить количественно, но этого не было сделано, а вывод прозвучал...

Тебе скучно и хочешь с кем-то поспорить?

У нас были разные мнения тогда, и до сих пор они разные - нет необходимости чтобы привести старую дискуссию и повторить снова все что уже было сказано.

pinko> У нас были разные мнения тогда, и до сих пор они разные

С твоим мнением я давно уже все понял.

pinko> нет необходимости чтобы привести старую дискуссию и повторить снова все что уже было сказано.

Есть необходимость дать остальным возможность разменять мнения на знания. Поэтому дискуссия будет не старая, а новая. Точнее будет наглядный расчет.

SashaMaks> 2. Векторная сумма всех сил относительно локальной системы отсчёта.
SashaMaks> 3. Многократная разница между модулями векторов силы тяги и силы тяжести.

Пример сложения двух векторов:
1. Результирующего вектора силы тяги и силы трения воздуха.
2. Вектора силы тяжести.
И расчёт для них погрешности при проецировании на локальную ось X'.

Для интервалов углов от 0° до 20° и тяговооруженности от 5 до 50 погрешность определения абсолютной величины ускорения на борту в средней точке траектории составит:

Угол: 0°; Тяговооруженность: 5 — ε = 100%*(400-400)/400 = 0,0%.
Угол: 0°; Тяговооруженность: 50 — ε = 100%*(4900-4900)/4900 = 0,0%.
Угол: 10°; Тяговооруженность: 5 — ε = 100%*(402,999-403,731)/403,731 = -0,0018%.
Угол: 10°; Тяговооруженность: 50 — ε = 100%*(4902,999-4903,059)/4903,059 = -0,0012%.
Угол: 20°; Тяговооруженность: 5 — ε = 100%*(411,171-413,728)/413,728 = -0,618%.*
Угол: 20°; Тяговооруженность: 50 — ε = 100%*(4911,171-4911,386)/4911,386 = -0,004%.

Как видно, точность определения ускорения много ниже 5%, что считается на практике высшей планкой по воспроизводимости результата.

• Приведен графический пример расчёта векторной суммы для наглядности.

SashaMaks> Есть необходимость дать остальным возможность разменять мнения на знания. Поэтому дискуссия будет не старая, а новая. Точнее будет наглядный расчет.

То есть хочешь с кем-то поспорить про теорию! Ты уже много раз сказал что у тебе есть рабочий физическую и математическую модель... Вместо того чтобы рисовать цветные картинки и теоретизировать почему по твоим словам БРЭО основаны только на 1D акселерометром должно будет работать так же хорошо или лучше, как и любой другой тип БРЭО:
- сделай прототип
- сделай несколько тестов вместе с надежным бортовыми компьютероми
- покажи установку и результаты
- докажи что всем ошибается, а ты прав

SashaMaks> 4. Распределение ускорений по длине траектории с учётом её кривизны.
SashaMaks> 5. Влияние изменения относительного угла поворота результирующего вектора на итоговую сумму и её погрешность.

Распределение типичной эпюры ускорений полёта ракеты по кривой траектории выглядит примерно так см. рис.

Площади S1 и S2 примерно равны и за счёт этого сумма ускорение в апогее стремиться к нулю.

Кривая подобного вида получается по данным одной оси датчика акселерометра за вычетом G или g.

При этом хорошо видно, что наибольшие значения ускорений находятся в зоне наименьшего наклона кривой, где присутствует наименьшая погрешность вычислений.

И обе площади, участвующие в сумме (в общем интеграле) имеют примерно одинаковую ошибку при суммировании ускорений от начала и до конца. Т.е. сколько изначально положительно недосуммировали почти столько же отрицательно недосуммируем.

Наклоны траектории присутствуют в обоих площадях и имеют некий средний угол наклона для каждой площади, разница между которыми настолько мала (угол А), что косинус этого угла очень близок к единице.

Поэтому суммирование до 0 идёт успешно и в пределах допустимой погрешности порядка не более 5% по высоте и скорости для самых наклонённых траекторий с низкой тяговооруженностью двигателей. Для обычных уклонений траекторий в пределах 0°-40° и я тяговооруженностью более 10, погрешность подсчёта скорости и нахождения апогея уже будет менее 1%.

Причём для нахождения апогея погрешность немного смещается за апогей из-за увеличения среднего угла наклона площади торможения относительно площади ускорений при увеличении угла наклона траектории полёта.

При строго вертикальном полёте апогей и ноль скорости находятся точно.

Скорость при наклонной траектории полёта вычисляется минимальная, так как при загибании траектории вниз, ракета уже начинает снова разгонятся, двигаясь дополнительно быстрее за счёт силы тяжести, проходя, тем самым, минимум скорости за апогеем.

pinko> Вместо того чтобы рисовать цветные картинки и теоретизировать почему по твоим словам

Ну ты же выкладываешь цветные картинки, почему я не могу привести свои чертежи?
Ты же пишешь недоказанные на практике свои словесные доводы, почему я не могу писать свои расчёты?

Что за двойные стандарты!?

SashaMaks> 6. Накопление ошибки всей суммы по всей длине траектории - интеграла ускорений.

И всё выше написанное сведенное в единый общий численный расчёт, который учитывает все главные особенности работы для такого типа датчика.

Ранее я уже писал об этом здесь:

Вот и полный исходный файл в экселе:

Там есть два типа симуляторов на первых двух листах - это для полёта вдоль одной оси и для полёта в плоскости XY.
Остальные три листа - это расчётная выборка для разных типов ракет, показывающая рабочее поле одноосевого датчика для трёх углов наклона траектории полёта в зависимости от УИ двигателя по топливу.

На последних 3х листах в графиках указаны по две соответствующие кривые одинакового цвета: моделируемой траектории полёта ракеты и интеграла (суммы) ускорений. Пересечение последней кривой оси X соответствует поиску апогея на кривой траектории.

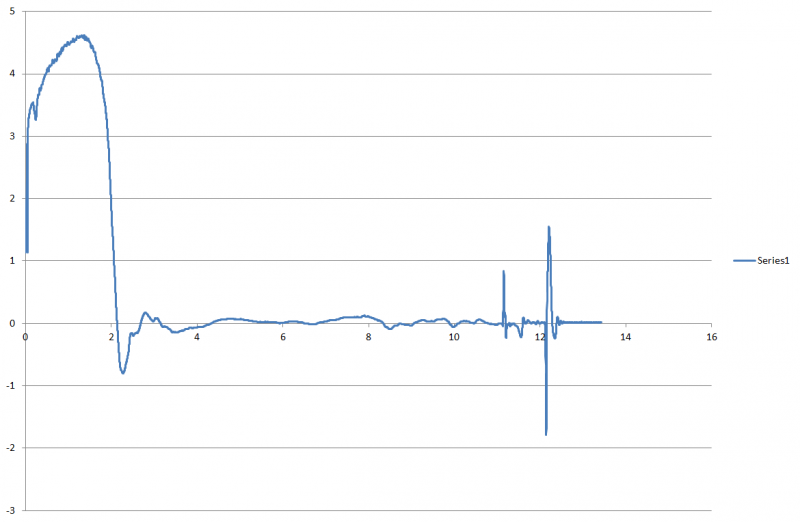
Вот и первый практический пример появился того, как успешно может работать данный алгоритм:

SashaMaks> Вот и первый практический пример появился того, как успешно может работать данный алгоритм:
Саша, но ведь регулярно бывает и вот так: