 Реклама Google — средство выживания форумов :)
Реклама Google — средство выживания форумов :)
-
![[image]](https://www.balancer.ru/cache/sites/i/m/img17.imageshack.us/img17/6421/128x128-crop/moonyo.png)
Что новенького про американцев на Луне
Теги:
aФон> Начните с себя.
Продолжу с вами.
Афон, а как там с правилом "сильнее толкаться" на скользкой поверхности? Разберем вашу шизику?
Продолжу с вами.
Афон, а как там с правилом "сильнее толкаться" на скользкой поверхности? Разберем вашу шизику?


aФон> Правильно, потому что этим прыгунам нужна максимальная высота, они там из-за высоты корячатся, на 120 см прыгают.
А на Луне никто не корячится. И прыгают совершенно без напряжения. Так, как на Земле ты даже от поверхности не оторвёшься (не превысишь силу тяжести).
aФон> Но мы, имея ВОЛШЕБНУЮ формулу h=ax-bx2
Вы имеете эпическую ахинею вместо мозгов. Вам уже миллион раз сказали, что так не считается работа мышц. Так считается пружина в вакууме
aФон> Можем вычислить, на какую они высоту будут прыгать, если уменьшить глубину приседа, но СОХРАНИВ ТЕХНИКУ.
Нет, не можете. Так мышцы не работают.
Вам сказали, что сила нужна ровно в 6 раз выше, чтобы сымитировать лунную гравитацию при ускорении видео. ТО есть, в 6 раз БОЛЕЕ РЕЗКИЕ ДВИЖЕНИЯ. Это невозможно по физиологическим причинам.
И Ваша теория о замедлении видео не подтверждается. После ускорения видео с Луны они не похожи на Земные условия. Наоборот, совершенно на них непохожи. Вы этот факт ИГНОРИРУЕТЕ, как и подобает сектанту.
aФон> Так мы получаем высоту их прыжка из 17 см приседа.
Нельзя прыгнуть из такого приседа вообще, не размахивая руками и не работая корпусом. А если это делать, то высота будет в лучшем случае сантиметров 10. И то вряд ли. Это физиология, с которой не поспоришь.
aФон> Не повторяйте эту ЧУШЬ, не надо.
Так не повторяйте. Вас тыкают носом, а вы флудите. ПРичём намеренно. Не отвечаете на вопросы по существу. Вы - тролль и флудер.
aФон> Это формулы из профильного института
Читаем первоисточник, который Вы переврали:
Русским по белому сказано, что это для случая предельных напряжений, чего нет на Луне. Там вообще нет никаких напряжений. Там лёгкие отталкивания без малейшего напряжения и без техники оптимального прыжка. И никаких ахинеистических формул тут нет.
aФон> Это было бы верно, если бы на Луне прыгали изо всей дури
А там никто так не прыгает. Там прыгают совершенно не напрягаясь. На Земле при такой технике и динамике прыжка человек ВООБЩЕ НЕ ОТОРВЁТСЯ ОТ ПОВЕРХНОСТИ.
aФон> Я с Вами и не спорю, на роликах прсед от 30 до 40 см (вместо 17)
Вы копипастите свой бред, в режиме "радиоточка с диджеем-попугаем".
aФон> Высота на роликах 100-120 см (у НАСА 42см)
Есть прыжки и выше метра. А по технике, где они прыгают даже на 20 сантиметров, на Земле невозможно оторваться от поверхности ВООБЩЕ, даже в одних трусах, я не говорю уже про скафандр. Это факт, который очевиден.
aФон> Именно поэтому, эти ролики надо пересчитывать с помощью формул
Формулы применяют к тому, механизм работы чего понятен. Вы же не понимаете элементарных принципов работы мышц и поэтому ваши формулы вообще неприменимы для данного случая.
aФон> Именно эту редукцию я и проводил чуть выше, превращая высокие прыжки из глубокого приседа в менее высокие из 17см приседа.
Что является ахинеей по причине непонимания механизма работы мышц и прогуливания физики за 6 класс.
А на Луне никто не корячится. И прыгают совершенно без напряжения. Так, как на Земле ты даже от поверхности не оторвёшься (не превысишь силу тяжести).
aФон> Но мы, имея ВОЛШЕБНУЮ формулу h=ax-bx2
Вы имеете эпическую ахинею вместо мозгов. Вам уже миллион раз сказали, что так не считается работа мышц. Так считается пружина в вакууме

aФон> Можем вычислить, на какую они высоту будут прыгать, если уменьшить глубину приседа, но СОХРАНИВ ТЕХНИКУ.
Нет, не можете. Так мышцы не работают.
Вам сказали, что сила нужна ровно в 6 раз выше, чтобы сымитировать лунную гравитацию при ускорении видео. ТО есть, в 6 раз БОЛЕЕ РЕЗКИЕ ДВИЖЕНИЯ. Это невозможно по физиологическим причинам.
И Ваша теория о замедлении видео не подтверждается. После ускорения видео с Луны они не похожи на Земные условия. Наоборот, совершенно на них непохожи. Вы этот факт ИГНОРИРУЕТЕ, как и подобает сектанту.
aФон> Так мы получаем высоту их прыжка из 17 см приседа.
Нельзя прыгнуть из такого приседа вообще, не размахивая руками и не работая корпусом. А если это делать, то высота будет в лучшем случае сантиметров 10. И то вряд ли. Это физиология, с которой не поспоришь.
aФон> Не повторяйте эту ЧУШЬ, не надо.
Так не повторяйте. Вас тыкают носом, а вы флудите. ПРичём намеренно. Не отвечаете на вопросы по существу. Вы - тролль и флудер.
aФон> Это формулы из профильного института
Читаем первоисточник, который Вы переврали:
Для определения этих коэффициентов используются только прыжки, выполненные с предельным (или околопредельным) напряжением сил. При использовании данных прыжков, выполненных в полсилы, не с полным использованием двигательного потенциала спортсмена" указанная выше закономерность взаимосвязи высоты прыжка с глубиной приседания может не прослеживаться, а результаты анализа таких прыжков не могут быть использованы на практике.
Русским по белому сказано, что это для случая предельных напряжений, чего нет на Луне. Там вообще нет никаких напряжений. Там лёгкие отталкивания без малейшего напряжения и без техники оптимального прыжка. И никаких ахинеистических формул тут нет.
aФон> Это было бы верно, если бы на Луне прыгали изо всей дури
А там никто так не прыгает. Там прыгают совершенно не напрягаясь. На Земле при такой технике и динамике прыжка человек ВООБЩЕ НЕ ОТОРВЁТСЯ ОТ ПОВЕРХНОСТИ.
aФон> Я с Вами и не спорю, на роликах прсед от 30 до 40 см (вместо 17)
Вы копипастите свой бред, в режиме "радиоточка с диджеем-попугаем".
aФон> Высота на роликах 100-120 см (у НАСА 42см)
Есть прыжки и выше метра. А по технике, где они прыгают даже на 20 сантиметров, на Земле невозможно оторваться от поверхности ВООБЩЕ, даже в одних трусах, я не говорю уже про скафандр. Это факт, который очевиден.
aФон> Именно поэтому, эти ролики надо пересчитывать с помощью формул
Формулы применяют к тому, механизм работы чего понятен. Вы же не понимаете элементарных принципов работы мышц и поэтому ваши формулы вообще неприменимы для данного случая.
aФон> Именно эту редукцию я и проводил чуть выше, превращая высокие прыжки из глубокого приседа в менее высокие из 17см приседа.
Что является ахинеей по причине непонимания механизма работы мышц и прогуливания физики за 6 класс.

aФон> Он на батуте скачет, а не приседает
Нет там никакого батута. ОН есть только в больной голове сектанта
Нет там никакого батута. ОН есть только в больной голове сектанта


aФон> Это легко доказывается, из условия равенства сил на Земле и Луне
Вот Вам и талдычат, что у вас ОШИБКА по причине не понимания физики за 6 класс. Мы видим на лунных видео совершенно иную картину, нежели это должно быть на Земле. Потому что силы равны. Нельзя при одинаковых усилиях сымитировать лунный прыжок. Для этого нужны силы, несуществующие в природе у представителей рода Хомо Сапиенс.
aФон> То есть сила мышц задействованная при прыжке на Луне в 42 см ЭКВИВАЛЕНТНА прыжку на Земле в 2.6 см
Уже больше похоже на правду А теперь подумайте, как надо прыгать на Земле для 42 сантиметров и пдумайте, при такой же технике прыжка на какую высоту улетел бы астронавт на Луне?
А теперь подумайте, как надо прыгать на Земле для 42 сантиметров и пдумайте, при такой же технике прыжка на какую высоту улетел бы астронавт на Луне?
aФон> [b]Таким образом, чтобы изобразить на Земле Луну от НАСА, надо развить силу толчка ВТРОЕ БОЛЬШУЮ, чем при земном прыжке на 2.6см
А вот тут ошибка. Вы опять путаете человеческое тело с пружиной в космосе
Вот Вам и талдычат, что у вас ОШИБКА по причине не понимания физики за 6 класс. Мы видим на лунных видео совершенно иную картину, нежели это должно быть на Земле. Потому что силы равны. Нельзя при одинаковых усилиях сымитировать лунный прыжок. Для этого нужны силы, несуществующие в природе у представителей рода Хомо Сапиенс.
aФон> То есть сила мышц задействованная при прыжке на Луне в 42 см ЭКВИВАЛЕНТНА прыжку на Земле в 2.6 см
Уже больше похоже на правду
 А теперь подумайте, как надо прыгать на Земле для 42 сантиметров и пдумайте, при такой же технике прыжка на какую высоту улетел бы астронавт на Луне?
А теперь подумайте, как надо прыгать на Земле для 42 сантиметров и пдумайте, при такой же технике прыжка на какую высоту улетел бы астронавт на Луне?aФон> [b]Таким образом, чтобы изобразить на Земле Луну от НАСА, надо развить силу толчка ВТРОЕ БОЛЬШУЮ, чем при земном прыжке на 2.6см
А вот тут ошибка. Вы опять путаете человеческое тело с пружиной в космосе


aФон> Скрипаль — Новичок, Пауэлл — пробирка, Башни-близнецы — Боинги, Сирия — химоруже Асада...
ZOG, Перун на вайтмарах с Асгарда, рептилоиды в пирамидах, Древние шумеры с гаплогруппой R1a, продолжайте, чего остановились то
ZOG, Перун на вайтмарах с Асгарда, рептилоиды в пирамидах, Древние шумеры с гаплогруппой R1a, продолжайте, чего остановились то


Итак, сектант упорно игнорирует интересные вопросы, задаваемые мной ему. Букду повторять их снова и снова.
1. Итак, аФон, скажите, почему ваша теория про замедление роликов в 2,45 раза не выдерживает проверки?
Почему при ускорении лунных видео в 2,45 раза мы видим ... ускоренное в 2,45 раза видео с неестественными невозможными движениями астронавтов в условиях именно Лунной гравитации и вакуума?
ВОт ПРУФ:

2. Как вы себе представляете "макет ровера размером 40 см" на фоне "имитатора грунта" с размером щебня "от 0,5 до 5 мм"? При таких соотношениях мы будем видеть не мелкодисперсную пыль, как на всех видео, а именно летящие булыжники. И как Вы сымитируете динамику движений при таких масштабах? Вы в курсе, что динамика при масштабировании не масштабируется?
3. Как можно прыгать, не напрягаясь, на такую высоту на Земле, при этом успевая размахивать ногами в скафандре во время подлёта несколько раз? Вы понимаете, что это на Земле НЕВОЗМОЖНО?
Apollo 16 Flat footed jumping and falling
This video shows Young and Duke jumping on the moon Duke miscalculates his jump and rotates backwards and falls on the PLSS. Some moon hoaxers ask why we don't see astronauts jumping around in the low gravity of the moon, well here they are, and duke sets a perfect example why you shouldn't free jump too high, especially with no hope of rescue or survival if you rip the suit And for any hoaxer who want's to play the "wires" card, a couple of things: Can you replicate Dukes jump, centre of rotation and fall with a wire?
Ответ на эти вопросы обязателен.
1. Итак, аФон, скажите, почему ваша теория про замедление роликов в 2,45 раза не выдерживает проверки?
Почему при ускорении лунных видео в 2,45 раза мы видим ... ускоренное в 2,45 раза видео с неестественными невозможными движениями астронавтов в условиях именно Лунной гравитации и вакуума?
ВОт ПРУФ:

Что новенького про американцев на Луне [Phazeus#20.04.18 18:02]
Проведём ЭКСПЕРИМЕНТ, как подобает здравомыслящим скептикам с научным складом мышления. Как утверждает представитель секты верующих в теорию заговора аФон, достаточно ускорить лунные видео в 2,45 раза, чтобы получить "типичные земные движения" астронавтов. Любой разумный человек понимает, что манипуляциями скоростью тут ничего сделать невозможно. Более того, не скорость главное, а динамика объектов и их взаимодействие. Но давайте возьмём один кусочек из какого-либо многочасового видео,…// Лунные космические программы2. Как вы себе представляете "макет ровера размером 40 см" на фоне "имитатора грунта" с размером щебня "от 0,5 до 5 мм"? При таких соотношениях мы будем видеть не мелкодисперсную пыль, как на всех видео, а именно летящие булыжники. И как Вы сымитируете динамику движений при таких масштабах? Вы в курсе, что динамика при масштабировании не масштабируется?
3. Как можно прыгать, не напрягаясь, на такую высоту на Земле, при этом успевая размахивать ногами в скафандре во время подлёта несколько раз? Вы понимаете, что это на Земле НЕВОЗМОЖНО?
Apollo 16 Flat footed jumping and falling
This video shows Young and Duke jumping on the moon Duke miscalculates his jump and rotates backwards and falls on the PLSS. Some moon hoaxers ask why we don't see astronauts jumping around in the low gravity of the moon, well here they are, and duke sets a perfect example why you shouldn't free jump too high, especially with no hope of rescue or survival if you rip the suit And for any hoaxer who want's to play the "wires" card, a couple of things: Can you replicate Dukes jump, centre of rotation and fall with a wire?
Ответ на эти вопросы обязателен.

aФон> Кто говорит, тупой Хэл?
aФон> Специалисты иного мнения
Так тебе же, барану, и написали:
ПРИ ПРОЧИХ РАВНЫХ УСЛОВИЯХ
Ты не смог эту строчку понять? А если понял, то зачем ты сюда приплел спортсменов, которые прыгают совершенно не так, как на лунных видео, и условия вообще ни разу не равные? Только потому что ты тупой или есть еще какие то причины?
aФон> Конечно, к идентичным, вклад рук и корпуса вычтем.
И как же ты их вычел? Где расчет вклада? Или ты свою тупую сектантскую веру сюда решил приплести?
aФон> Почему не изменится, от них есть помощь, но она не велика.
Это твоя тупая сектантская религия так утверждает?
aФон> Я учел работу корпуса, не нервничайте.
aФон> Учёл с запасом, по максимуму, вычитая 20% от высоты прыжка.
aФон> То, что это максимум, можете прочитать у экспертов
И где ты там прочитал про корпус? Или ты настолько тупой, что не понял, что там идет речь не про установление рекорда высоты, а про постановку прыжка для игры в волейбол?
аФон, как можно так лажать? Нет. Как можно быть таким тупым?
aФон> Это формула h=ax-bx2, которую группа товарищей из ВНИИФК, ГШВСМ проверила на большой аудитории испытуемых.
Вот только один тупой сектант применяет её не к тем людям, не к тем прыжкам, не к тем действиям и т.д. Да еще и не видит, что его тупые расчеты вообще никак не относятся к реальности. И не хочет ничего проверять сам. Правильно. Зачем ему проверять? Его тупой расчет уложился в его тупую религию. А на соответствие реальности можно и начхать.
aФон> В корне неверная постановка вопроса.
В каком месте она не верная? Почему она не верная? Только потому что она не нравится одному тупому сектанту или есть еще какие причины?
aФон> Выдумка про 6 раз предполагает, что дело происходит на Луне, а это не так.
Ты совсем что ли тупой?
Я тебе уже сто раз объяснял. Для имитации лунного прыжка на Земле при идентичных движениях нужно обладать не менее чем в 6 раз большей силой ног, чем астронавт.
Что здесь не так? Ты с чем то не согласен? С чем?
aФон> Не повторяйте эту ЧУШЬ, не надо.
Почему чушь? Потому что ломает тупую религию тупому сектанту?
aФон> Это было бы верно, если бы на Луне прыгали изо всей дури и была бы МАКСИМАЛЬНАЯ лунная высота, но ничего такого нет. Есть земная высота ролика и всё.
Причем тут высота, баран? Тебе про что говорят? Про усилие отталкивания.
aФон> ∫Fз(x)dx = mgh+mgX (Работа силы мышц пошла на высоту прыжка на Земле и подъем из приседа)
aФон> ∫Fл(x)dx = 2mgh/6+2mgX/6 (Работа силы мышц пошла на высоту прыжка на Луне и подъем из приседа)
aФон> Из этих уравнений получаем
aФон> ∫Fз(x)dx=∫3Fл(x)dx
aФон> То есть силу мышцы должны развивать усилие втрое сильнее, чем при прыжке на Луне на ту же высоту.
А двойки в лунной формуле ты пририсовал специально чтобы у тебя 3 получилось?
aФон> Специалисты иного мнения
Так тебе же, барану, и написали:
Наши модельные., лабораторные и педагогические исследования прыжков в высоту с места показали, что при прочих равных условиях
ПРИ ПРОЧИХ РАВНЫХ УСЛОВИЯХ
Ты не смог эту строчку понять? А если понял, то зачем ты сюда приплел спортсменов, которые прыгают совершенно не так, как на лунных видео, и условия вообще ни разу не равные? Только потому что ты тупой или есть еще какие то причины?
aФон> Конечно, к идентичным, вклад рук и корпуса вычтем.
И как же ты их вычел? Где расчет вклада? Или ты свою тупую сектантскую веру сюда решил приплести?
aФон> Почему не изменится, от них есть помощь, но она не велика.
Это твоя тупая сектантская религия так утверждает?
aФон> Я учел работу корпуса, не нервничайте.
aФон> Учёл с запасом, по максимуму, вычитая 20% от высоты прыжка.
aФон> То, что это максимум, можете прочитать у экспертов
И где ты там прочитал про корпус? Или ты настолько тупой, что не понял, что там идет речь не про установление рекорда высоты, а про постановку прыжка для игры в волейбол?
аФон, как можно так лажать? Нет. Как можно быть таким тупым?
aФон> Это формула h=ax-bx2, которую группа товарищей из ВНИИФК, ГШВСМ проверила на большой аудитории испытуемых.
Вот только один тупой сектант применяет её не к тем людям, не к тем прыжкам, не к тем действиям и т.д. Да еще и не видит, что его тупые расчеты вообще никак не относятся к реальности. И не хочет ничего проверять сам. Правильно. Зачем ему проверять? Его тупой расчет уложился в его тупую религию. А на соответствие реальности можно и начхать.
aФон> В корне неверная постановка вопроса.
В каком месте она не верная? Почему она не верная? Только потому что она не нравится одному тупому сектанту или есть еще какие причины?
aФон> Выдумка про 6 раз предполагает, что дело происходит на Луне, а это не так.
Ты совсем что ли тупой?
Я тебе уже сто раз объяснял. Для имитации лунного прыжка на Земле при идентичных движениях нужно обладать не менее чем в 6 раз большей силой ног, чем астронавт.
Что здесь не так? Ты с чем то не согласен? С чем?
aФон> Не повторяйте эту ЧУШЬ, не надо.
Почему чушь? Потому что ломает тупую религию тупому сектанту?
aФон> Это было бы верно, если бы на Луне прыгали изо всей дури и была бы МАКСИМАЛЬНАЯ лунная высота, но ничего такого нет. Есть земная высота ролика и всё.
Причем тут высота, баран? Тебе про что говорят? Про усилие отталкивания.
aФон> ∫Fз(x)dx = mgh+mgX (Работа силы мышц пошла на высоту прыжка на Земле и подъем из приседа)
aФон> ∫Fл(x)dx = 2mgh/6+2mgX/6 (Работа силы мышц пошла на высоту прыжка на Луне и подъем из приседа)
aФон> Из этих уравнений получаем
aФон> ∫Fз(x)dx=∫3Fл(x)dx
aФон> То есть силу мышцы должны развивать усилие втрое сильнее, чем при прыжке на Луне на ту же высоту.
А двойки в лунной формуле ты пририсовал специально чтобы у тебя 3 получилось?



korneyy:
Заканчиваем с баранами.; предупреждение (+1) по категории «Переход на личности»
Xan> Батут!
Xan> Американцы привезли на Луну батут!
Полагаю, все гораздо хуже было.
Как-то по такому сценарию: Эксперимент с подушкой безопасности смотреть онлайн видео от Я снимаю... в хорошем качестве.
Xan> Американцы привезли на Луну батут!
Полагаю, все гораздо хуже было.
Как-то по такому сценарию: Эксперимент с подушкой безопасности смотреть онлайн видео от Я снимаю... в хорошем качестве.


- korneyy [21.04.2018 17:32]: Предупреждение пользователю: Hal#21.04.18 11:30
3-62> Афон, а как там с правилом "сильнее толкаться" на скользкой поверхности? Разберем вашу шизику?
Что Вам не нравится?
Что Вам не нравится?
Сцепление на Луне уменьшится в 6 раз из-за снижения веса (для сравнения, - на Земле сцепление резины на льду хуже, чем на сухом асфальте в 8-9 раз). Однако, так ли это при лунном прыжке? Адекватно ли сравнение со скользкой поверхностью?
При высоком прыжке производится сильный толчок, и увеличивается давление на грунт за счет силы толчка, поэтому сцепление с грунтом возрастает по мере роста высоты прыжка (именно поэтому на Луне астронавтов тренировали перемещаться прыжками, а не ходить обычным способом). Например, если средняя сила толчка астронавта равна 2Mg, то по сравнению с его весом на Луне (равном Mg/6) сила давления увеличивается в 12 раз, и во столько же увеличивается сцепление с грунтом. Толчок равный по силе земному компенсирует снижение сцепления вызванное малым весом астронавта.
Таким образом, для высоких прыжков проблемы сцепления не существует. Однако лунные прыжки на малую высоту можно сравнить с земными прыжками на скользком льду - коэффициент трения на Луне около 0.7, поэтому сила трения равна 0.7Mg/6 ~ 0.1Mg т.е. как на Земле на льду. Ролики НАСА в основном и содержат низкие прыжки астронавтов (5-15 см), но на них нет и намека на слабое сцепление с грунтом.
http://mo---on.narod.ru/


Hal> Так тебе же, барану, и написали:
Hal>
Hal> ПРИ ПРОЧИХ РАВНЫХ УСЛОВИЯХ
Я же и не спорил, что "ПРИ ПРОЧИХ РАВНЫХ УСЛОВИЯХ".
Hal> Ты не смог эту строчку понять? А если понял, то зачем ты сюда приплел спортсменов, которые прыгают совершенно не так, как на лунных видео, и условия вообще ни разу не равные? Только потому что ты тупой или есть еще какие то причины?
С чего Вы взяли, что не понял, а зачем же тогда я 20% высоты вычитал, как Вы думаете?
Hal> И как же ты их вычел? Где расчет вклада?
Есть эксперименты, в которых это установили, я на них ссылался.
Hal> И где ты там прочитал про корпус? Или ты настолько тупой, что не понял, что там идет речь не про установление рекорда высоты, а про постановку прыжка для игры в волейбол?
Да, там идет речь о высоте прыжка вверх при игре в волейбол
Hal> Я тебе уже сто раз объяснял. Для имитации лунного прыжка на Земле при идентичных движениях нужно обладать не менее чем в 6 раз большей силой ног, чем астронавт.
Это Ваше невежество, нет никаких шести раз.
Hal> Причем тут высота, баран? Тебе про что говорят? Про усилие отталкивания.
aФон>> ∫Fз(x)dx = mgh+mgX (Работа силы мышц пошла на высоту прыжка на Земле и подъем из приседа)
aФон>> ∫Fл(x)dx = 2mgh/6+2mgX/6 (Работа силы мышц пошла на высоту прыжка на Луне и подъем из приседа)
aФон>> Из этих уравнений получаем
aФон>> ∫Fз(x)dx=∫3Fл(x)dx
aФон>> То есть силу мышцы должны развивать усилие втрое сильнее, чем при прыжке на Луне на ту же высоту.
Hal> А двойки в лунной формуле ты пририсовал специально чтобы у тебя 3 получилось?
Двойка - это двойная масса. На Земле актер прыгает со своей массой тела, чтобы имитировать прыжок на Луне с ДВОЙНОЙ массой (тело+скафандр)
Hal>
Наши модельные., лабораторные и педагогические исследования прыжков в высоту с места показали, что при прочих равных условиях
Hal> ПРИ ПРОЧИХ РАВНЫХ УСЛОВИЯХ
Я же и не спорил, что "ПРИ ПРОЧИХ РАВНЫХ УСЛОВИЯХ".
Hal> Ты не смог эту строчку понять? А если понял, то зачем ты сюда приплел спортсменов, которые прыгают совершенно не так, как на лунных видео, и условия вообще ни разу не равные? Только потому что ты тупой или есть еще какие то причины?
С чего Вы взяли, что не понял, а зачем же тогда я 20% высоты вычитал, как Вы думаете?
Hal> И как же ты их вычел? Где расчет вклада?
Есть эксперименты, в которых это установили, я на них ссылался.
Hal> И где ты там прочитал про корпус? Или ты настолько тупой, что не понял, что там идет речь не про установление рекорда высоты, а про постановку прыжка для игры в волейбол?
Да, там идет речь о высоте прыжка вверх при игре в волейбол
Hal> Я тебе уже сто раз объяснял. Для имитации лунного прыжка на Земле при идентичных движениях нужно обладать не менее чем в 6 раз большей силой ног, чем астронавт.
Это Ваше невежество, нет никаких шести раз.
Hal> Причем тут высота, баран? Тебе про что говорят? Про усилие отталкивания.
aФон>> ∫Fз(x)dx = mgh+mgX (Работа силы мышц пошла на высоту прыжка на Земле и подъем из приседа)
aФон>> ∫Fл(x)dx = 2mgh/6+2mgX/6 (Работа силы мышц пошла на высоту прыжка на Луне и подъем из приседа)
aФон>> Из этих уравнений получаем
aФон>> ∫Fз(x)dx=∫3Fл(x)dx
aФон>> То есть силу мышцы должны развивать усилие втрое сильнее, чем при прыжке на Луне на ту же высоту.
Hal> А двойки в лунной формуле ты пририсовал специально чтобы у тебя 3 получилось?

Двойка - это двойная масса. На Земле актер прыгает со своей массой тела, чтобы имитировать прыжок на Луне с ДВОЙНОЙ массой (тело+скафандр)


Phazeus> Вот Вам и талдычат, что у вас ОШИБКА по причине не понимания физики за 6 класс. Мы видим на лунных видео совершенно иную картину, нежели это должно быть на Земле. Потому что силы равны. Нельзя при одинаковых усилиях сымитировать лунный прыжок. Для этого нужны силы, несуществующие в природе у представителей рода Хомо Сапиенс.
Вам не надо ничего ТАЛДЫЧИТЬ, Вы не знаете закона сохранения энергии и, вероятно, уже никогда не узнаете.
aФон>> То есть сила мышц задействованная при прыжке на Луне в 42 см ЭКВИВАЛЕНТНА прыжку на Земле в 2.6 см
Phazeus> Уже больше похоже на правду А теперь подумайте, как надо прыгать на Земле для 42 сантиметров и пдумайте, при такой же технике прыжка на какую высоту улетел бы астронавт на Луне?
А теперь подумайте, как надо прыгать на Земле для 42 сантиметров и пдумайте, при такой же технике прыжка на какую высоту улетел бы астронавт на Луне?
На луне астронавт улетел бы на высоту 3*42+2*17 = 160см
То есть, если атлета, запечатленного на ролике НАСА, послать на Луну и попросить применить то же самое усилие, как на этом земном видеоролике (изображающем якобы Янга), то на Луне он прыгнет на 160 см в скафандре.
aФон>> [b]Таким образом, чтобы изобразить на Земле Луну от НАСА, надо развить силу толчка ВТРОЕ БОЛЬШУЮ, чем при земном прыжке на 2.6см
Phazeus> А вот тут ошибка. Вы опять путаете человеческое тело с пружиной в космосе
Учите закон сохранения энергии.
Вам не надо ничего ТАЛДЫЧИТЬ, Вы не знаете закона сохранения энергии и, вероятно, уже никогда не узнаете.
aФон>> То есть сила мышц задействованная при прыжке на Луне в 42 см ЭКВИВАЛЕНТНА прыжку на Земле в 2.6 см
Phazeus> Уже больше похоже на правду
 А теперь подумайте, как надо прыгать на Земле для 42 сантиметров и пдумайте, при такой же технике прыжка на какую высоту улетел бы астронавт на Луне?
А теперь подумайте, как надо прыгать на Земле для 42 сантиметров и пдумайте, при такой же технике прыжка на какую высоту улетел бы астронавт на Луне?На луне астронавт улетел бы на высоту 3*42+2*17 = 160см
То есть, если атлета, запечатленного на ролике НАСА, послать на Луну и попросить применить то же самое усилие, как на этом земном видеоролике (изображающем якобы Янга), то на Луне он прыгнет на 160 см в скафандре.
aФон>> [b]Таким образом, чтобы изобразить на Земле Луну от НАСА, надо развить силу толчка ВТРОЕ БОЛЬШУЮ, чем при земном прыжке на 2.6см
Phazeus> А вот тут ошибка. Вы опять путаете человеческое тело с пружиной в космосе

Учите закон сохранения энергии.


aФон>> Но мы, имея ВОЛШЕБНУЮ формулу h=ax-bx2
Phazeus> Вы имеете эпическую ахинею вместо мозгов. Вам уже миллион раз сказали, что так не считается работа мышц. Так считается пружина в вакууме
Причем тут пружина? Объясните, наконец, откуда Вы взяли пружину вообще?
aФон>> Можем вычислить, на какую они высоту будут прыгать, если уменьшить глубину приседа, но СОХРАНИВ ТЕХНИКУ.
Phazeus> Нет, не можете. Так мышцы не работают.
Это экспериментальный факт, найденный в опытах
Phazeus> Вам сказали, что сила нужна ровно в 6 раз выше,
Кто сказал? Невежда, который закон сохранения не знает?
Phazeus> Нельзя прыгнуть из такого приседа вообще, не размахивая руками и не работая корпусом. А если это делать, то высота будет в лучшем случае сантиметров 10. И то вряд ли. Это физиология, с которой не поспоришь.
Это Вы о се6е сказали? Готов согласится. Если Вы со всей дури маша руками из 30 см приседа можете прыгнуть на 20 см, тогда для Вас верна формула:
h=ax-bx2 = 1,33x-0,22x2
Из 17см приседа, маша руками, Вы прыгните на 16 см, а если не будете махать руками, то прыгните на 13см.
Вы не годитесь в актеры для съемок лунной аферы.
aФон>> Это формулы из профильного института
Phazeus> Читаем первоисточник, который Вы переврали:
Phazeus> Русским по белому сказано, что это для случая предельных напряжений, чего нет на Луне. Там вообще нет никаких напряжений.
Я же и не спорю, что ЭТО ДЛЯ ПРЕДЕЛЬНЫХ НАПРЯЖЕНИЙ
Phazeus> А там никто так не прыгает. Там прыгают совершенно не напрягаясь. На Земле при такой технике и динамике прыжка человек ВООБЩЕ НЕ ОТОРВЁТСЯ ОТ ПОВЕРХНОСТИ.
Это Вам ВЕРА подсказывает?
А я дал расчет, на Земле это было бы 2.6 см.
Phazeus> Есть прыжки и выше метра.
Нет таких прыжков. Есть всего два высоких, но не свободных прыжка - батутный и на кабине ЛМ, всё.
Только лохи могут после этого факта свято верить в Луну, или троли на зарплате, дочки офицеров вещать эту ахинею про высадку.
Phazeus> Формулы применяют к тому, механизм работы чего понятен.
Если бы Вы где-нибудь, когда-нибудь учились, то знали бы, что формулы могут быть ad hoc, то есть найденные экспериментальным способом для конкретной задачи.
Phazeus> Вы имеете эпическую ахинею вместо мозгов. Вам уже миллион раз сказали, что так не считается работа мышц. Так считается пружина в вакууме

Причем тут пружина? Объясните, наконец, откуда Вы взяли пружину вообще?
aФон>> Можем вычислить, на какую они высоту будут прыгать, если уменьшить глубину приседа, но СОХРАНИВ ТЕХНИКУ.
Phazeus> Нет, не можете. Так мышцы не работают.
Это экспериментальный факт, найденный в опытах
Phazeus> Вам сказали, что сила нужна ровно в 6 раз выше,
Кто сказал? Невежда, который закон сохранения не знает?
Phazeus> Нельзя прыгнуть из такого приседа вообще, не размахивая руками и не работая корпусом. А если это делать, то высота будет в лучшем случае сантиметров 10. И то вряд ли. Это физиология, с которой не поспоришь.
Это Вы о се6е сказали? Готов согласится. Если Вы со всей дури маша руками из 30 см приседа можете прыгнуть на 20 см, тогда для Вас верна формула:
h=ax-bx2 = 1,33x-0,22x2
Из 17см приседа, маша руками, Вы прыгните на 16 см, а если не будете махать руками, то прыгните на 13см.
Вы не годитесь в актеры для съемок лунной аферы.
aФон>> Это формулы из профильного института
Phazeus> Читаем первоисточник, который Вы переврали:
Phazeus> Русским по белому сказано, что это для случая предельных напряжений, чего нет на Луне. Там вообще нет никаких напряжений.
Я же и не спорю, что ЭТО ДЛЯ ПРЕДЕЛЬНЫХ НАПРЯЖЕНИЙ
Phazeus> А там никто так не прыгает. Там прыгают совершенно не напрягаясь. На Земле при такой технике и динамике прыжка человек ВООБЩЕ НЕ ОТОРВЁТСЯ ОТ ПОВЕРХНОСТИ.
Это Вам ВЕРА подсказывает?
А я дал расчет, на Земле это было бы 2.6 см.
Phazeus> Есть прыжки и выше метра.
Нет таких прыжков. Есть всего два высоких, но не свободных прыжка - батутный и на кабине ЛМ, всё.
Только лохи могут после этого факта свято верить в Луну, или троли на зарплате, дочки офицеров вещать эту ахинею про высадку.
Phazeus> Формулы применяют к тому, механизм работы чего понятен.
Если бы Вы где-нибудь, когда-нибудь учились, то знали бы, что формулы могут быть ad hoc, то есть найденные экспериментальным способом для конкретной задачи.


Это сообщение редактировалось 21.04.2018 в 20:36
Сектант упорно игнорирует интересные вопросы, задаваемые мной ему. Букду повторять их снова и снова.
1. Итак, аФон, скажите, почему ваша теория про замедление роликов в 2,45 раза не выдерживает проверки?
Почему при ускорении лунных видео в 2,45 раза мы видим ... ускоренное в 2,45 раза видео с неестественными невозможными движениями астронавтов в условиях именно Лунной гравитации и вакуума?
ВОт ПРУФ:

2. Как вы себе представляете "макет ровера размером 40 см" на фоне "имитатора грунта" с размером щебня "от 0,5 до 5 мм"? При таких соотношениях мы будем видеть не мелкодисперсную пыль, как на всех видео, а именно летящие булыжники. И как Вы сымитируете динамику движений при таких масштабах? Вы в курсе, что динамика при масштабировании не масштабируется?
3. Как можно прыгать, не напрягаясь, на такую высоту на Земле, при этом успевая размахивать ногами в скафандре во время подлёта несколько раз? Вы понимаете, что это на Земле НЕВОЗМОЖНО?
Apollo 16 Flat footed jumping and falling
This video shows Young and Duke jumping on the moon Duke miscalculates his jump and rotates backwards and falls on the PLSS. Some moon hoaxers ask why we don't see astronauts jumping around in the low gravity of the moon, well here they are, and duke sets a perfect example why you shouldn't free jump too high, especially with no hope of rescue or survival if you rip the suit And for any hoaxer who want's to play the "wires" card, a couple of things: Can you replicate Dukes jump, centre of rotation and fall with a wire?
Ответ на эти вопросы обязателен.
1. Итак, аФон, скажите, почему ваша теория про замедление роликов в 2,45 раза не выдерживает проверки?
Почему при ускорении лунных видео в 2,45 раза мы видим ... ускоренное в 2,45 раза видео с неестественными невозможными движениями астронавтов в условиях именно Лунной гравитации и вакуума?
ВОт ПРУФ:

Что новенького про американцев на Луне [Phazeus#20.04.18 18:02]
Проведём ЭКСПЕРИМЕНТ, как подобает здравомыслящим скептикам с научным складом мышления. Как утверждает представитель секты верующих в теорию заговора аФон, достаточно ускорить лунные видео в 2,45 раза, чтобы получить "типичные земные движения" астронавтов. Любой разумный человек понимает, что манипуляциями скоростью тут ничего сделать невозможно. Более того, не скорость главное, а динамика объектов и их взаимодействие. Но давайте возьмём один кусочек из какого-либо многочасового видео,…// Лунные космические программы2. Как вы себе представляете "макет ровера размером 40 см" на фоне "имитатора грунта" с размером щебня "от 0,5 до 5 мм"? При таких соотношениях мы будем видеть не мелкодисперсную пыль, как на всех видео, а именно летящие булыжники. И как Вы сымитируете динамику движений при таких масштабах? Вы в курсе, что динамика при масштабировании не масштабируется?
3. Как можно прыгать, не напрягаясь, на такую высоту на Земле, при этом успевая размахивать ногами в скафандре во время подлёта несколько раз? Вы понимаете, что это на Земле НЕВОЗМОЖНО?
Apollo 16 Flat footed jumping and falling
This video shows Young and Duke jumping on the moon Duke miscalculates his jump and rotates backwards and falls on the PLSS. Some moon hoaxers ask why we don't see astronauts jumping around in the low gravity of the moon, well here they are, and duke sets a perfect example why you shouldn't free jump too high, especially with no hope of rescue or survival if you rip the suit And for any hoaxer who want's to play the "wires" card, a couple of things: Can you replicate Dukes jump, centre of rotation and fall with a wire?
Ответ на эти вопросы обязателен.

Phazeus> Почему при ускорении лунных видео в 2,45 раза мы видим ... ускоренное в 2,45 раза видео с неестественными невозможными движениями астронавтов в условиях именно Лунной гравитации и вакуума?
Потому что в НАСА не идиоты сидели и знали, что шевелится при съемках надо шустрее, чтобы после их замедления в 2.5 раза не было ощущения столбняка, напавшего на астронавтов на Луне.
Phazeus> 2. Как вы себе представляете "макет ровера размером 40 см" на фоне "имитатора грунта" с размером щебня "от 0,5 до 5 мм"? При таких соотношениях мы будем видеть не мелкодисперсную пыль, как на всех видео, а именно летящие булыжники.
Песчинка 5мм с расстояния 5-10 м имеет угловые размеры меньше, чем разрешение фотопленки, поэтому не имеет никакого значения ее размер, если она меньше чем "пиксел пленки", то она - мелкодисперсную пыль
Phazeus> 3. Как можно прыгать, не напрягаясь, на такую высоту на Земле, при этом успевая размахивать ногами в скафандре во время подлёта несколько раз? Вы понимаете, что это на Земле НЕВОЗМОЖНО?
Это же на батуте, тут вообще не о чем говорить, потому и не видны ноги, чтобы не вылез в кадр батут
Потому что в НАСА не идиоты сидели и знали, что шевелится при съемках надо шустрее, чтобы после их замедления в 2.5 раза не было ощущения столбняка, напавшего на астронавтов на Луне.
Phazeus> 2. Как вы себе представляете "макет ровера размером 40 см" на фоне "имитатора грунта" с размером щебня "от 0,5 до 5 мм"? При таких соотношениях мы будем видеть не мелкодисперсную пыль, как на всех видео, а именно летящие булыжники.
Песчинка 5мм с расстояния 5-10 м имеет угловые размеры меньше, чем разрешение фотопленки, поэтому не имеет никакого значения ее размер, если она меньше чем "пиксел пленки", то она - мелкодисперсную пыль
Phazeus> 3. Как можно прыгать, не напрягаясь, на такую высоту на Земле, при этом успевая размахивать ногами в скафандре во время подлёта несколько раз? Вы понимаете, что это на Земле НЕВОЗМОЖНО?
Это же на батуте, тут вообще не о чем говорить, потому и не видны ноги, чтобы не вылез в кадр батут


Phazeus>> Почему при ускорении лунных видео в 2,45 раза мы видим ... ускоренное в 2,45 раза видео с неестественными невозможными движениями астронавтов в условиях именно Лунной гравитации и вакуума?
aФон> Потому что в НАСА не идиоты сидели и знали, что шевелится при съемках надо шустрее
ТЫ видео видел? Это сделали "не идиоты в НАСА", заставив людей двигаться как гигантские блохи, с невозможной в природе динамикой, чтобы потом это видео замедлить в 2,45 раза, так?
Вот я ускорил один кусочек из ДЕСЯТКОВ ЧАСОВ ВИДЕО (не идиоты НАСА даже не догадались, что не нужно снимать столько видео, когда его можно было не делать вообще), при этом движения совершенно не выглядят земными. Более того, они выглядят СОВЕРШЕННО НЕВОЗМОЖНЫМИ. Вообще НИГДЕ.
Так что все ваши рассуждения в топку. Это НЕВОЗМОЖНО.
aФон> Песчинка 5мм с расстояния 5-10 м имеет угловые размеры меньше, чем разрешение фотопленки
Какие угловые размеры будет иметь 40см ровер с расстояния "5-10 метров"? ЧТо-то мы видим ровер в непосредственной близости.
С КАКОГО РАССТОЯНИЯ СНИМАЛСЯ "макет ровера 40 см"?
Если рассуждать так, то тут нет и одного метра, съёмка "макета" тогда производится с расстояний ДО 1 метра.
ЩЕБЕНЬ ДОЛЖЕН БЫТЬ ВИДЕН!
Может тогда макет был, но был размерами больше в несколько раз? Наоборот, увеличен?
aФон> Это же на батуте, тут вообще не о чем говорить, потому и не видны ноги, чтобы не вылез в кадр батут
Нет там никаких батутов. ДЕСЯТКИ ЧАСОВ ВИДЕО. Многие сцены вообще доступны с РАЗНЫХ КАМЕР, с разных ракурсов. Везде они прыгают, отбрасывают вееры пыли, качают маятники, кидают пакетами по вакууму, отжимаются, отталкиваясь от луны и подлетая просто от толчка рукой.
Вы способны объяснить ВСЕ ЭТИ ДЕСЯТКИ ЧАСОВ ВИДЕО? Я ведь буду вас долбить, пока все эти десятки часов тут не разберём.
А батут есть только в воображении параноидального сектанта
aФон> Потому что в НАСА не идиоты сидели и знали, что шевелится при съемках надо шустрее
ТЫ видео видел? Это сделали "не идиоты в НАСА", заставив людей двигаться как гигантские блохи, с невозможной в природе динамикой, чтобы потом это видео замедлить в 2,45 раза, так?
Вот я ускорил один кусочек из ДЕСЯТКОВ ЧАСОВ ВИДЕО (не идиоты НАСА даже не догадались, что не нужно снимать столько видео, когда его можно было не делать вообще), при этом движения совершенно не выглядят земными. Более того, они выглядят СОВЕРШЕННО НЕВОЗМОЖНЫМИ. Вообще НИГДЕ.
Так что все ваши рассуждения в топку. Это НЕВОЗМОЖНО.
aФон> Песчинка 5мм с расстояния 5-10 м имеет угловые размеры меньше, чем разрешение фотопленки
Какие угловые размеры будет иметь 40см ровер с расстояния "5-10 метров"? ЧТо-то мы видим ровер в непосредственной близости.
С КАКОГО РАССТОЯНИЯ СНИМАЛСЯ "макет ровера 40 см"?
Если рассуждать так, то тут нет и одного метра, съёмка "макета" тогда производится с расстояний ДО 1 метра.
ЩЕБЕНЬ ДОЛЖЕН БЫТЬ ВИДЕН!
Может тогда макет был, но был размерами больше в несколько раз? Наоборот, увеличен?
aФон> Это же на батуте, тут вообще не о чем говорить, потому и не видны ноги, чтобы не вылез в кадр батут
Нет там никаких батутов. ДЕСЯТКИ ЧАСОВ ВИДЕО. Многие сцены вообще доступны с РАЗНЫХ КАМЕР, с разных ракурсов. Везде они прыгают, отбрасывают вееры пыли, качают маятники, кидают пакетами по вакууму, отжимаются, отталкиваясь от луны и подлетая просто от толчка рукой.
Вы способны объяснить ВСЕ ЭТИ ДЕСЯТКИ ЧАСОВ ВИДЕО? Я ведь буду вас долбить, пока все эти десятки часов тут не разберём.
А батут есть только в воображении параноидального сектанта


aФон> Что Вам не нравится?
Правило нелепое и неверное. Оно не приводит к повышению устойчивости. Оно приводит лишь к ускорению потери контроля над положением тела.
Не понимаете это?
Что минимизировать "проскальзывание" можно лишь уменьшив угол отклонения силы от вертикали, но не изменяя величину этой силы. Никак не доходит сей факт до вашего понимания?
Правило нелепое и неверное. Оно не приводит к повышению устойчивости. Оно приводит лишь к ускорению потери контроля над положением тела.
Не понимаете это?
Что минимизировать "проскальзывание" можно лишь уменьшив угол отклонения силы от вертикали, но не изменяя величину этой силы. Никак не доходит сей факт до вашего понимания?


3-62> Что минимизировать "проскальзывание" можно лишь уменьшив угол отклонения силы от вертикали, но не изменяя величину этой силы. Никак не доходит сей факт до вашего понимания?
Конечно, два фактора влияют, отклонение от вертикали и величина силы.
Чем ближе к вертикали и чем больше сила, тем выше сила трения. Именно поэтому на тренажерах-имитаторах лунной гравитации и был найден ОПТИМАЛЬНЫЙ способ перемещения - заячьи прыжки, но на роликах их высота не соответствует Луне.
Александр Гордон Американцы не были на Луне!
Дополнительно: Secret Nasa - Real Footage! https://www.youtube.com/watch?v=kFAZoVGxqY4 канал "Did man walk on the moon?":https://www.youtube.com/user/moonfakery/videos?view=0 Чтобы предотвратить бесконечные попытки назвать неверящих в «лунные миссии NASA» шизофрениками и прочими псевдобольными: https://www.youtube.com/watch?v=WNBA3lMO1y0
Конечно, два фактора влияют, отклонение от вертикали и величина силы.
Чем ближе к вертикали и чем больше сила, тем выше сила трения. Именно поэтому на тренажерах-имитаторах лунной гравитации и был найден ОПТИМАЛЬНЫЙ способ перемещения - заячьи прыжки, но на роликах их высота не соответствует Луне.
Александр Гордон Американцы не были на Луне!
Дополнительно: Secret Nasa - Real Footage! https://www.youtube.com/watch?v=kFAZoVGxqY4 канал "Did man walk on the moon?":https://www.youtube.com/user/moonfakery/videos?view=0 Чтобы предотвратить бесконечные попытки назвать неверящих в «лунные миссии NASA» шизофрениками и прочими псевдобольными: https://www.youtube.com/watch?v=WNBA3lMO1y0


aФон> Конечно, два фактора влияют, отклонение от вертикали и величина силы.
Давай формулу, афон - гдЕ видно будет "влияние величины силы".
aФон> Чем ближе к вертикали и чем сильнее сила, тем выше сила трения.
Сущеглупый вывод. При углах близких к 90 sin практически не меняется. Так что сила трения будет все та же.
Давай формулу, афон - гдЕ видно будет "влияние величины силы".
aФон> Чем ближе к вертикали и чем сильнее сила, тем выше сила трения.
Сущеглупый вывод. При углах близких к 90 sin практически не меняется. Так что сила трения будет все та же.


Phazeus> ТЫ видео видел? Это сделали "не идиоты в НАСА", заставив людей двигаться как гигантские блохи, с невозможной в природе динамикой, чтобы потом это видео замедлить в 2,45 раза, так?
Послушайте, "невозможной динамикой" к делу не пришьешь.
Любое движение Вы можете спокойно выполнить в 2-2.5 раза быстрее, даже не тренируясь, а там были подготовленные атлеты, которые все 6 экспедиций со съемочной площадки не вылазили, о чём Вы вообще говорите (надеюсь, Вы понимаете, что это не астронавты на съемку приезжали)
Phazeus> Вот я ускорил один кусочек из ДЕСЯТКОВ ЧАСОВ ВИДЕО (не идиоты НАСА даже не догадались, что не нужно снимать столько видео, когда его можно было не делать вообще), при этом движения совершенно не выглядят земными. Более того, они выглядят СОВЕРШЕННО НЕВОЗМОЖНЫМИ.
Это эмоции....
Phazeus> Так что все ваши рассуждения в топку. Это НЕВОЗМОЖНО.
По какому ИЗМЕРЯЕМОМУ ПАРАМЕТРУ невозможно?
Phazeus> Какие угловые размеры будет иметь 40см ровер с расстояния "5-10 метров"? ЧТо-то мы видим ровер в непосредственной близости.
Несколько метров - это достаточно близко для макета, но не для песчинки.
Phazeus> С КАКОГО РАССТОЯНИЯ СНИМАЛСЯ "макет ровера 40 см"?
С разного, от 5м до 25м, наверное.
Phazeus> ЩЕБЕНЬ ДОЛЖЕН БЫТЬ ВИДЕН!
Как Вы его увидите, если он покрашен реголитом?
Phazeus> Может тогда макет был, но был размерами больше в несколько раз? Наоборот, увеличен?
Нет, на том ролике он именно уменьшен. Это связано с размерами павильона, ведь павильон нужно было освещать. Поэтому площадка по которой он ездит метров 20, а весь круг метров 40 диаметром
Phazeus> Нет там никаких батутов. ДЕСЯТКИ ЧАСОВ ВИДЕО. Многие сцены вообще доступны с РАЗНЫХ КАМЕР, с разных ракурсов. Везде они прыгают,
Нет там РОВНО ДВА высоких прыжка, этот батутный и на кабине ЛМ, больше нет.
Phazeus> Вы способны объяснить ВСЕ ЭТИ ДЕСЯТКИ ЧАСОВ ВИДЕО? Я ведь буду вас долбить, пока все эти десятки часов тут не разберём.
Конечно, там единая технология на все ролики
Phazeus> А батут есть только в воображении параноидального сектанта
Батут видели?
Сравните с роликом НАСА
Батут - от базы до сложных связок | eurotramp.com
Данные видео помогут вам освоить прыжки на батуте, от базовых до продвинутых. Сайт правообладателя:https://www.eurotramp.com
Послушайте, "невозможной динамикой" к делу не пришьешь.
Любое движение Вы можете спокойно выполнить в 2-2.5 раза быстрее, даже не тренируясь, а там были подготовленные атлеты, которые все 6 экспедиций со съемочной площадки не вылазили, о чём Вы вообще говорите (надеюсь, Вы понимаете, что это не астронавты на съемку приезжали)
Phazeus> Вот я ускорил один кусочек из ДЕСЯТКОВ ЧАСОВ ВИДЕО (не идиоты НАСА даже не догадались, что не нужно снимать столько видео, когда его можно было не делать вообще), при этом движения совершенно не выглядят земными. Более того, они выглядят СОВЕРШЕННО НЕВОЗМОЖНЫМИ.
Это эмоции....
Phazeus> Так что все ваши рассуждения в топку. Это НЕВОЗМОЖНО.
По какому ИЗМЕРЯЕМОМУ ПАРАМЕТРУ невозможно?
Phazeus> Какие угловые размеры будет иметь 40см ровер с расстояния "5-10 метров"? ЧТо-то мы видим ровер в непосредственной близости.
Несколько метров - это достаточно близко для макета, но не для песчинки.
Phazeus> С КАКОГО РАССТОЯНИЯ СНИМАЛСЯ "макет ровера 40 см"?
С разного, от 5м до 25м, наверное.
Phazeus> ЩЕБЕНЬ ДОЛЖЕН БЫТЬ ВИДЕН!
Как Вы его увидите, если он покрашен реголитом?
Phazeus> Может тогда макет был, но был размерами больше в несколько раз? Наоборот, увеличен?
Нет, на том ролике он именно уменьшен. Это связано с размерами павильона, ведь павильон нужно было освещать. Поэтому площадка по которой он ездит метров 20, а весь круг метров 40 диаметром

Phazeus> Нет там никаких батутов. ДЕСЯТКИ ЧАСОВ ВИДЕО. Многие сцены вообще доступны с РАЗНЫХ КАМЕР, с разных ракурсов. Везде они прыгают,
Нет там РОВНО ДВА высоких прыжка, этот батутный и на кабине ЛМ, больше нет.
Phazeus> Вы способны объяснить ВСЕ ЭТИ ДЕСЯТКИ ЧАСОВ ВИДЕО? Я ведь буду вас долбить, пока все эти десятки часов тут не разберём.
Конечно, там единая технология на все ролики
Phazeus> А батут есть только в воображении параноидального сектанта

Батут видели?
Сравните с роликом НАСА
Батут - от базы до сложных связок | eurotramp.com
Данные видео помогут вам освоить прыжки на батуте, от базовых до продвинутых. Сайт правообладателя:https://www.eurotramp.com


aФон> Послушайте, "невозможной динамикой" к делу не пришьешь.
Де я вижу, что сектанту пофиг всё
То есть, плевать, что ИЗ ВАШИХ СОБСТВЕННЫХ ЗАЯВЛЕНИЙ следует проверяемый вывод, который НЕ ПОДТВЕРЖДАЕТСЯ ПРАКТИКОЙ и ошибочен? Вас это не смущает?
Если не смущает, то Вы сектант, кондовый мракобес
По буквам: при ускорении роликов в 2,45 раза мы не только не наблюдаем "земные движения", но наблюдаем просто невозможные нигде ни при каких условиях движения. Ваша теория про замедление видео для имитации Луны неверна.
Это факт.
aФон> Любое движение Вы можете спокойно выполнить в 2-2.5 раза быстрее, даже не тренируясь
Это практически невозможно. Можно выполнить одно простое движение, НО НЕ ДЕСЯТКИ ЧАСОВ САМЫХ СЛОЖНЫХ ДВИЖЕНИЙ, как, например, вышеприведённые мной ролики.
Очевидно даже ослу, что это НЕВОЗМОЖНО.
А для сектанта возможно всё?
Слив.
aФон> Это эмоции....
Это факты, на которые сектанту нечего ответить Слив.
Слив.
aФон> По какому ИЗМЕРЯЕМОМУ ПАРАМЕТРУ невозможно?
По техниук движений и по динамике. Если мы говорим про движения астронавтов. А также невозможно по полёту предметов в вакууме (на Земле это не сымитировать) и нельзя сымитировать качением маятников на фоне движения людей.
И нельзя сделать то, что я показал на своём видео. Он просто УБИЙСТВЕННЫЙ для вас.
На нём 100 видно, что это никак не может быть движениями людей. А это лишь маленький отрывок, меньше минуты, из ДЕСЯТКОВ ЧАСОВ ВИДЕО, которые ВСЕ такие.
Слив вам
aФон> Несколько метров - это достаточно близко для макета, но не для песчинки.
Снова нечего ответить и мямлите невпопад?
Рядом с макетом 40см щебень будет казаться не просто щебнем (он таковым даже на оригинальном масштабе будет казаться), он будет просто кирпичами. Нельзя снимать крупным планом 40см макет ровера на фоне щебня, который выглядит как мелкодисперсная пыль, практически как дым.
Тут ваше предположение неверно. Слив.
aФон> С разного, от 5м до 25м, наверное.
Мы видим на видео ровер с расстояние не превышающего длину его корпуса или пары-тройки корпусов. Это в пересчёте на ваши фантазии дат от несятка сантиметров до полутора метров,щебень должен качаться булыжниками, вылетающими из-под колёс.
А это я ещё не затронул тему динамики движений, которая при масштабировании не сохраняется, она совершенно разная на разных масштабах.
Я так понял, что вам нечего сказать. Мямлите. Слив.
aФон> Как Вы его увидите, если он покрашен реголитом?
Чего?



На видео мы прекрасно видим реголит. Пыль, а не булыжники, которые при таком масштабировании должны казаться как сантиметровые камни
aФон> Нет, на том ролике он именно уменьшен
Тогда отказывайтесь от веры в отобранный и покрашенный щебень. На видео мы никакого щебня не видим, даже при съёмке вплотную к роверу и астронавтам.
aФон> Нет там РОВНО ДВА высоких прыжка, этот батутный и на кабине ЛМ
Там нет батутов Бабуты мерещатся только тупорылым сектантам
Бабуты мерещатся только тупорылым сектантам 
Прыжков там дохрена. Готовы разбирать со мной трёхчасовое видео?
Принимаете вызов? Я буду бить больно, на поражение
aФон> Батут видели?
Я же сказал, батуты видят только тупорылые сектанты. У них такое свойство, видеть то, чего нет Вон, Елхов не даст соврать
Вон, Елхов не даст соврать 
аФон> Сравните с роликом НАСА
Прекрасный пример полностью различной техники В ролике с Луны мы не видим никакого батута, там и места нет под него
В ролике с Луны мы не видим никакого батута, там и места нет под него  А он должен быть огромным, так как астронавт ходит. При ходьбе он ступает по твёрдой поверхности
А он должен быть огромным, так как астронавт ходит. При ходьбе он ступает по твёрдой поверхности  Вам придётся придумать какой-то мегабатутик, который будет следовать за движениями астронавта, имитируя в нужный момент твёрдую поверхность
Вам придётся придумать какой-то мегабатутик, который будет следовать за движениями астронавта, имитируя в нужный момент твёрдую поверхность 
При этом мы видим то, что ДОЛЖНО БЫТЬ НА Луне И только сектантская вера может заставлять параноика плодить сущности без причины
И только сектантская вера может заставлять параноика плодить сущности без причины 
Де я вижу, что сектанту пофиг всё

То есть, плевать, что ИЗ ВАШИХ СОБСТВЕННЫХ ЗАЯВЛЕНИЙ следует проверяемый вывод, который НЕ ПОДТВЕРЖДАЕТСЯ ПРАКТИКОЙ и ошибочен? Вас это не смущает?
Если не смущает, то Вы сектант, кондовый мракобес

По буквам: при ускорении роликов в 2,45 раза мы не только не наблюдаем "земные движения", но наблюдаем просто невозможные нигде ни при каких условиях движения. Ваша теория про замедление видео для имитации Луны неверна.
Это факт.
aФон> Любое движение Вы можете спокойно выполнить в 2-2.5 раза быстрее, даже не тренируясь
Это практически невозможно. Можно выполнить одно простое движение, НО НЕ ДЕСЯТКИ ЧАСОВ САМЫХ СЛОЖНЫХ ДВИЖЕНИЙ, как, например, вышеприведённые мной ролики.
Очевидно даже ослу, что это НЕВОЗМОЖНО.
А для сектанта возможно всё?

Слив.
aФон> Это эмоции....
Это факты, на которые сектанту нечего ответить
 Слив.
Слив.aФон> По какому ИЗМЕРЯЕМОМУ ПАРАМЕТРУ невозможно?
По техниук движений и по динамике. Если мы говорим про движения астронавтов. А также невозможно по полёту предметов в вакууме (на Земле это не сымитировать) и нельзя сымитировать качением маятников на фоне движения людей.
И нельзя сделать то, что я показал на своём видео. Он просто УБИЙСТВЕННЫЙ для вас.
На нём 100 видно, что это никак не может быть движениями людей. А это лишь маленький отрывок, меньше минуты, из ДЕСЯТКОВ ЧАСОВ ВИДЕО, которые ВСЕ такие.
Слив вам

aФон> Несколько метров - это достаточно близко для макета, но не для песчинки.
Снова нечего ответить и мямлите невпопад?
Рядом с макетом 40см щебень будет казаться не просто щебнем (он таковым даже на оригинальном масштабе будет казаться), он будет просто кирпичами. Нельзя снимать крупным планом 40см макет ровера на фоне щебня, который выглядит как мелкодисперсная пыль, практически как дым.
Тут ваше предположение неверно. Слив.
aФон> С разного, от 5м до 25м, наверное.
Мы видим на видео ровер с расстояние не превышающего длину его корпуса или пары-тройки корпусов. Это в пересчёте на ваши фантазии дат от несятка сантиметров до полутора метров,щебень должен качаться булыжниками, вылетающими из-под колёс.
А это я ещё не затронул тему динамики движений, которая при масштабировании не сохраняется, она совершенно разная на разных масштабах.
Я так понял, что вам нечего сказать. Мямлите. Слив.
aФон> Как Вы его увидите, если он покрашен реголитом?
Чего?




На видео мы прекрасно видим реголит. Пыль, а не булыжники, которые при таком масштабировании должны казаться как сантиметровые камни

aФон> Нет, на том ролике он именно уменьшен
Тогда отказывайтесь от веры в отобранный и покрашенный щебень. На видео мы никакого щебня не видим, даже при съёмке вплотную к роверу и астронавтам.
aФон> Нет там РОВНО ДВА высоких прыжка, этот батутный и на кабине ЛМ
Там нет батутов
 Бабуты мерещатся только тупорылым сектантам
Бабуты мерещатся только тупорылым сектантам 
Прыжков там дохрена. Готовы разбирать со мной трёхчасовое видео?

Принимаете вызов? Я буду бить больно, на поражение

aФон> Батут видели?
Я же сказал, батуты видят только тупорылые сектанты. У них такое свойство, видеть то, чего нет
 Вон, Елхов не даст соврать
Вон, Елхов не даст соврать 
аФон> Сравните с роликом НАСА
Прекрасный пример полностью различной техники
 В ролике с Луны мы не видим никакого батута, там и места нет под него
В ролике с Луны мы не видим никакого батута, там и места нет под него  А он должен быть огромным, так как астронавт ходит. При ходьбе он ступает по твёрдой поверхности
А он должен быть огромным, так как астронавт ходит. При ходьбе он ступает по твёрдой поверхности  Вам придётся придумать какой-то мегабатутик, который будет следовать за движениями астронавта, имитируя в нужный момент твёрдую поверхность
Вам придётся придумать какой-то мегабатутик, который будет следовать за движениями астронавта, имитируя в нужный момент твёрдую поверхность 
При этом мы видим то, что ДОЛЖНО БЫТЬ НА Луне
 И только сектантская вера может заставлять параноика плодить сущности без причины
И только сектантская вера может заставлять параноика плодить сущности без причины 

 Реклама Google — средство выживания форумов :)
Реклама Google — средство выживания форумов :)
Phazeus> По буквам: при ускорении роликов в 2,45 раза мы не только не наблюдаем "земные движения", но наблюдаем просто невозможные нигде ни при каких условиях движения.
Это Ваши девичьи мечты. "Невозможные" - это не формализованный параметр, его нельзя померить, а потому это из области пускания соплей....
aФон>> Любое движение Вы можете спокойно выполнить в 2-2.5 раза быстрее, даже не тренируясь
Phazeus> Это практически невозможно. Можно выполнить одно простое движение, НО НЕ ДЕСЯТКИ ЧАСОВ САМЫХ СЛОЖНЫХ ДВИЖЕНИЙ, как, например, вышеприведённые мной ролики.
Ваш пустой треп меня утомил. Давайте сделаем так, возьмите секундомер и засеките сколько секунд вы тратите, например, на то, чтобы поднести чашку ко рту. Теперь повторите это движение в 2 раза быстрее, потом в три раза быстрее, фиксируйте секундомером....
Phazeus> Очевидно даже ослу, что это НЕВОЗМОЖНО.
Ослам вроде Вас и доказывать ничего не надо, Вы и так проглотите...
aФон>> По какому ИЗМЕРЯЕМОМУ ПАРАМЕТРУ невозможно?
Phazeus> По техниук движений и по динамике. Если мы говорим про движения астронавтов.
Это неформализованный параметр, это сопли, это нельзя померить
Phazeus> А также невозможно по полёту предметов в вакууме (на Земле это не сымитировать) и нельзя сымитировать качением маятников на фоне движения людей.
Можно. Маятнику надо добавить грузик, тогда он будет дольше качаться, а в перо вставить металлический стержень, тогда оно упадет вместе с молотком.
Phazeus> И нельзя сделать то, что я показал на своём видео. Он просто УБИЙСТВЕННЫЙ для вас.
Это какое?
Phazeus> На нём 100 видно, что это никак не может быть движениями людей.
А чьими, обезьянними?
Phazeus> Рядом с макетом 40см щебень будет казаться не просто щебнем (он таковым даже на оригинальном масштабе будет казаться), он будет просто кирпичами. Нельзя снимать крупным планом 40см макет ровера на фоне щебня, который выглядит как мелкодисперсная пыль, практически как дым.
1. Щебень мелкий 5-15мм
2. Покрашен имитатором реголита, то есть очень бархатистый
Phazeus> Мы видим на видео ровер с расстояние не превышающего длину его корпуса или пары-тройки корпусов.
Вам кажется.
Phazeus> А это я ещё не затронул тему динамики движений, которая при масштабировании не сохраняется, она совершенно разная на разных масштабах.
У меня об этом подробно расписано на сайте
Phazeus> На видео мы прекрасно видим реголит. Пыль, а не булыжники, которые при таком масштабировании должны казаться как сантиметровые камни
Как они могут казаться камнями, если это 5мм песчинки с бархатистой поверхностью?
Phazeus> Прыжков там дохрена. Готовы разбирать со мной трёхчасовое видео?
Уже все до Вас разобрали. Прыжков там ровно ДВА, удовлетворяюших лунной высоте, - это батутный и на ЛМ.
Phazeus> Прекрасный пример полностью различной техники В ролике с Луны мы не видим никакого батута, там и места нет под него
В ролике с Луны мы не видим никакого батута, там и места нет под него  А он должен быть огромным, так как астронавт ходит. При ходьбе он ступает по твёрдой поверхности
А он должен быть огромным, так как астронавт ходит. При ходьбе он ступает по твёрдой поверхности  Вам придётся придумать какой-то мегабатутик, который будет следовать за движениями астронавта, имитируя в нужный момент твёрдую поверхность
Вам придётся придумать какой-то мегабатутик, который будет следовать за движениями астронавта, имитируя в нужный момент твёрдую поверхность 
Он ходит от батута к батуту.
Это Ваши девичьи мечты. "Невозможные" - это не формализованный параметр, его нельзя померить, а потому это из области пускания соплей....
aФон>> Любое движение Вы можете спокойно выполнить в 2-2.5 раза быстрее, даже не тренируясь
Phazeus> Это практически невозможно. Можно выполнить одно простое движение, НО НЕ ДЕСЯТКИ ЧАСОВ САМЫХ СЛОЖНЫХ ДВИЖЕНИЙ, как, например, вышеприведённые мной ролики.
Ваш пустой треп меня утомил. Давайте сделаем так, возьмите секундомер и засеките сколько секунд вы тратите, например, на то, чтобы поднести чашку ко рту. Теперь повторите это движение в 2 раза быстрее, потом в три раза быстрее, фиксируйте секундомером....
Phazeus> Очевидно даже ослу, что это НЕВОЗМОЖНО.
Ослам вроде Вас и доказывать ничего не надо, Вы и так проглотите...
aФон>> По какому ИЗМЕРЯЕМОМУ ПАРАМЕТРУ невозможно?
Phazeus> По техниук движений и по динамике. Если мы говорим про движения астронавтов.
Это неформализованный параметр, это сопли, это нельзя померить
Phazeus> А также невозможно по полёту предметов в вакууме (на Земле это не сымитировать) и нельзя сымитировать качением маятников на фоне движения людей.
Можно. Маятнику надо добавить грузик, тогда он будет дольше качаться, а в перо вставить металлический стержень, тогда оно упадет вместе с молотком.
Phazeus> И нельзя сделать то, что я показал на своём видео. Он просто УБИЙСТВЕННЫЙ для вас.
Это какое?
Phazeus> На нём 100 видно, что это никак не может быть движениями людей.
А чьими, обезьянними?
Phazeus> Рядом с макетом 40см щебень будет казаться не просто щебнем (он таковым даже на оригинальном масштабе будет казаться), он будет просто кирпичами. Нельзя снимать крупным планом 40см макет ровера на фоне щебня, который выглядит как мелкодисперсная пыль, практически как дым.
1. Щебень мелкий 5-15мм
2. Покрашен имитатором реголита, то есть очень бархатистый
Phazeus> Мы видим на видео ровер с расстояние не превышающего длину его корпуса или пары-тройки корпусов.
Вам кажется.
Phazeus> А это я ещё не затронул тему динамики движений, которая при масштабировании не сохраняется, она совершенно разная на разных масштабах.
У меня об этом подробно расписано на сайте
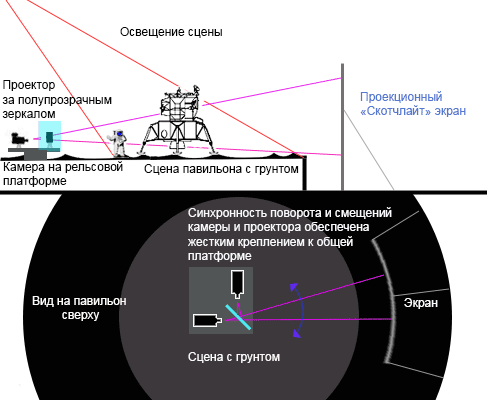
Нет никакой возможности отличить замедленный земной ролик с ровером или его макетом, скорость которого в 2.45/√n (здесь n - коэффициент, масштабирования) больше скорости лунного ровера, - частички "пыли" будут лететь полностью идентично. Чтобы это доказать рассмотрим нисходящую ветку баллистической траектории вылетевшей из под колес ровера или макета (уменьшенной в n раз копии ровера) частицы щебня (от точки макс. высоты до падения):
(28) yм=Gt2/2
(29) xм=Vмt
Vм - это горизонтальная компонента скорости (вдоль оси Х) частицы, вылетающей из под колес макета.
G - земное ускорение свободного падения
Растянем координатную систему в n раз, чтобы размер макета совпал с оригиналом:
(30) y=nyм=nGt2/2
(31) x=nxм=nVмt
Выразив t через x (31) и, подставив в (30), получим уравнения параболы (ось Y ориентирована от точки макс высоты вниз) для песчинки:
(32) y=nGx2/(2n2Vм2)=(G/(nVм2))x2/2
Для частиц от ровера на Луне справедливо:
(33) y=gt2/2
(34) x=Vлt
(35) y=(g/Vл2)x2/2
g - лунное ускорение свободного падения
Vл - горизонтальная компонента скорости на Луне
Из (35) и (32) получаем, что параболы траекторий полета песчинок будут идентичны, если:
(36) g/Vл2=G/(nVм2)
(37) Vм=Vл√(G/ng)=2.45Vл/√n
То есть макет должен двигаться со скоростью больше лунной в 2.45/√n . Чтобы определить коэффициент замедления видеоролика подставим в (31) значение Vм из (37).
(38) x=nVмt = 2.45nVлt/√n =2.45√n Vлt
Из сравнения с (34) находим коэффициент замедления видеоролика - 2.45√n
Если в съемках используется полноразмерный ровер (n=1), то ролик, замедленный в √(G/g)=2.45, дает полную иллюзию лунной траектории для частиц, вылетающих из под колес в 2.45 раза более быстрого земного ровера.
Для макета коэффициент замедления равен 2.45√n , в частности, если используется макет в шесть раз более мелкий, чем ровер (n=6), то его скорость должна быть равной лунной, а видеоролик нужно замедлить в 6 раз.
http://mo---on.narod.ru/
Phazeus> На видео мы прекрасно видим реголит. Пыль, а не булыжники, которые при таком масштабировании должны казаться как сантиметровые камни

Как они могут казаться камнями, если это 5мм песчинки с бархатистой поверхностью?
Phazeus> Прыжков там дохрена. Готовы разбирать со мной трёхчасовое видео?

Уже все до Вас разобрали. Прыжков там ровно ДВА, удовлетворяюших лунной высоте, - это батутный и на ЛМ.
Phazeus> Прекрасный пример полностью различной техники
 В ролике с Луны мы не видим никакого батута, там и места нет под него
В ролике с Луны мы не видим никакого батута, там и места нет под него  А он должен быть огромным, так как астронавт ходит. При ходьбе он ступает по твёрдой поверхности
А он должен быть огромным, так как астронавт ходит. При ходьбе он ступает по твёрдой поверхности  Вам придётся придумать какой-то мегабатутик, который будет следовать за движениями астронавта, имитируя в нужный момент твёрдую поверхность
Вам придётся придумать какой-то мегабатутик, который будет следовать за движениями астронавта, имитируя в нужный момент твёрдую поверхность 
Он ходит от батута к батуту.


Это сообщение редактировалось 21.04.2018 в 23:20
Copyright © Balancer 1997..2024
Создано 05.03.2005
Связь с владельцами и администрацией сайта: anonisimov@gmail.com, rwasp1957@yandex.ru и admin@balancer.ru.
Создано 05.03.2005
Связь с владельцами и администрацией сайта: anonisimov@gmail.com, rwasp1957@yandex.ru и admin@balancer.ru.
 aФон
aФон

 инфо
инфо инструменты
инструменты


 Xan
Xan






