-
/11-web.jpg)
РДТТ конструкции технологии материалы - XV
Теги:
SashaPro, я не в курсе насчёт Бернулли, но твои расчёты этого двигателя противоречат не только опыту любителей, но и книжкам. Поэтому я склонен не доверять твоим результатам расчётов ;^))
Советую поскорее сделать какой-нибудь стенд и начать испытания.
Советую поскорее сделать какой-нибудь стенд и начать испытания.
Serge77> SashaPro, я не в курсе насчёт Бернулли, но твои расчёты этого двигателя противоречат не только опыту любителей, но и книжкам. Поэтому я склонен не доверять твоим результатам расчётов ;^))
Знаю, заметил, но если учесть такую беду у обычной карамельной шашки, как эрозионное горение у основания заряда, которое приводит к сильному конусу профиля канала из-за большого напора, вызванного огромной скорость горения топлива, то всё вполне согласуется. При этом кстати тоже возможно постоянство тяги в центре графика. Просто более плавный выход на постоянство и сход с него (очень важно учесть плавность относительно всего времени работы двигателя).
Serge77> Советую поскорее сделать какой-нибудь стенд и начать испытания.
Ну это не проблема, уже занимаюсь...
Знаю, заметил, но если учесть такую беду у обычной карамельной шашки, как эрозионное горение у основания заряда, которое приводит к сильному конусу профиля канала из-за большого напора, вызванного огромной скорость горения топлива, то всё вполне согласуется. При этом кстати тоже возможно постоянство тяги в центре графика. Просто более плавный выход на постоянство и сход с него (очень важно учесть плавность относительно всего времени работы двигателя).
Serge77> Советую поскорее сделать какой-нибудь стенд и начать испытания.
Ну это не проблема, уже занимаюсь...
Ещё раз повторю: согласно опыту любителей и книжкам в этом двигателе не должно быть эрозионного горения. При любом топливе.
Serge77> Ещё раз повторю: согласно опыту любителей и книжкам в этом двигателе не должно быть эрозионного горения. При любом топливе.
Если его там быть не должно, тогда из-за перепада давлений, горение закончится раньше вверху и там корпус быстро почернеет или даже прогорит, если и перепада давлений быть не должно по длине канала, тогда просто любители обманываются компенсацией этих факторов. пока что я ещё не видел, точных экспериментальных данных значений давления по длине канала. А эрозия впонле может быть и горит ровно по цилиндрической поверхности, из-за чего и кажется, что давление одинаковое.
Если его там быть не должно, тогда из-за перепада давлений, горение закончится раньше вверху и там корпус быстро почернеет или даже прогорит, если и перепада давлений быть не должно по длине канала, тогда просто любители обманываются компенсацией этих факторов. пока что я ещё не видел, точных экспериментальных данных значений давления по длине канала. А эрозия впонле может быть и горит ровно по цилиндрической поверхности, из-за чего и кажется, что давление одинаковое.
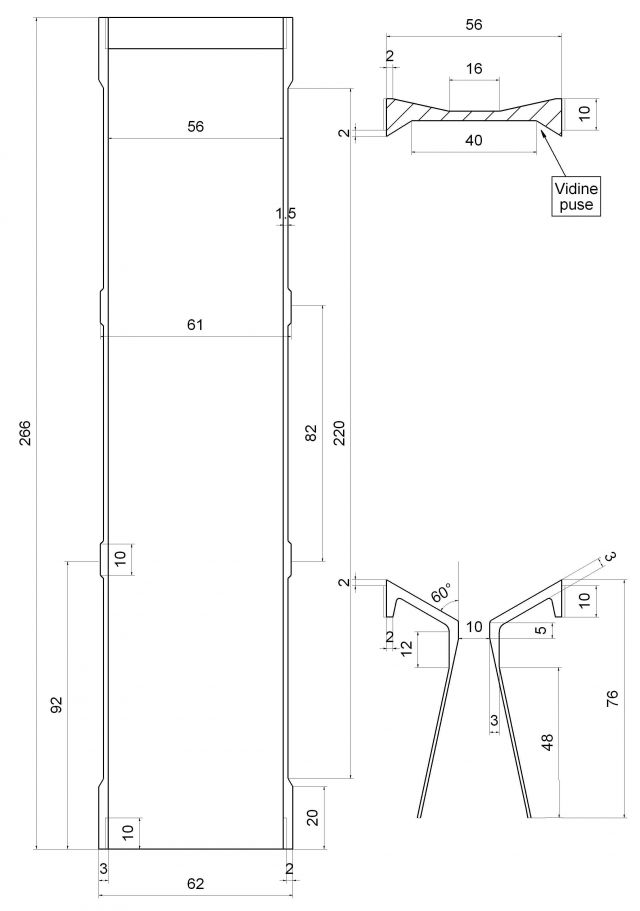
Второй двигатель с секторным разделённым зарядом готов к заправке.
Прикреплённые файлы:
Непонятно, будет ли крестовина чем-то отделена от топлива? Будет ли на получаемых секциях бронировка?
Serge77> Непонятно, будет ли крестовина чем-то отделена от топлива? Будет ли на получаемых секциях бронировка?
Бумажными листами топливо будет отделяться с боков, а где поверхность стерженя, будет селитровая бумага. Они сами прижмуться к оправке при заправке топливом. А в начале будут лишь фиксированы сверху, чтобы несползли.
Бумажными листами топливо будет отделяться с боков, а где поверхность стерженя, будет селитровая бумага. Они сами прижмуться к оправке при заправке топливом. А в начале будут лишь фиксированы сверху, чтобы несползли.
Зазор между секциями довольно большой, там нужна нормальная бронировка, одного слоя бумаги может не хватить (смотря какая бумага конечно).
А с корпусом топливо будет скреплено?
А с корпусом топливо будет скреплено?
Serge77> Зазор между секциями довольно большой, там нужна нормальная бронировка, одного слоя бумаги может не хватить (смотря какая бумага конечно).
Serge77> А с корпусом топливо будет скреплено?
Скреплено будет обязательно или смысл всего этого. А вот, что за зазор, я не понял. Тут бронировка нужна ровно так, чтобы закрыть щель которая и без того будет очень маленькой <0,05мм.
P.S. Двигатель заправляется в два этапа по две секции с помощью двух оправок. При этом после заправки первых двух секторов, нужно выждать пару часов, чтобы топливо схватило, после чего оно само уже будет частью второй оправки.
Serge77> А с корпусом топливо будет скреплено?
Скреплено будет обязательно или смысл всего этого. А вот, что за зазор, я не понял. Тут бронировка нужна ровно так, чтобы закрыть щель которая и без того будет очень маленькой <0,05мм.
P.S. Двигатель заправляется в два этапа по две секции с помощью двух оправок. При этом после заправки первых двух секторов, нужно выждать пару часов, чтобы топливо схватило, после чего оно само уже будет частью второй оправки.
А, теперь понял. Я думал, ширина щели будет такая, как толщина лепестков вставки.
Читаю книжку выложенную Атмосфера. Меня интересовало почему же для разгона газа при дозвуковой скорости канал нужно сужать, а для разгона сверзвукового газа нужно разширять канал. Формулы которые там приведены дают объяснение, но самой сути процесса я не понимаю. Что мешает газу разгоняться до сверхзвуковой скорости в сужающемся канале?
Есть ли где-нибудь упрощенная методика расчета формы сопла?
Есть ли где-нибудь упрощенная методика расчета формы сопла?
www.kirov-rockets.ru
kirya> Меня интересовало почему же для разгона газа при дозвуковой скорости канал нужно сужать, а для разгона сверзвукового газа нужно разширять канал.
Ну попытаюсь объяснить. Скорость звука описывает термодинамическое состояние газа. Чем больше внутренняя энергия газа и чем меньше его молекулярный вес, тем больше будет скорость звука. А скорость звука обусловлена хаотичным движением молекул, так вот если газ не расширяется, то как он может разогнаться быстрее скорости звука или, что тоже самое, потратить больше энергии чем в нём есть. То, что нужно сужать - это просто закон бернулли, в данном случае одинаково справедлив для всего, что течёт.
kirya> Формулы которые там приведены дают объяснение, но самой сути процесса я не понимаю. Что мешает газу разгоняться до сверхзвуковой скорости в сужающемся канале?
А мешает ему в этом закон распределения Максвела. Молекулы движуться хаотично, и есть, которые движуться с максимальной скоростью и есть те, которые вообще не движуться. Поэтому есть среднее значение скорости газа. Однако газ в замкнутом пространстве не вдижется. При появлении дырки с перепадом давлений, газ начинается ускоряться, появляется течение. А при подходе к минимальному сечению в канале, молекулы начинают двигаться примерно в одном направлении, но ещё очень значительно число молекул движущихся в противоположном направлении потоку. Что означает возможность передачи звуковых колебаний от дырки внутрь камеры.
Короче молекулы при подходе к минимальному сечению, движуться во всех направлениях, а после они уже не могут двигаться против потока. При этом их перпендикулярные оси движения скорости падают, и молекулы движуться преимущественно в одном направлении приближаясь к макисмально возможной скорости, определяемой внутренней энергией газа.
Понимать это надо так, что всё до дырки - это сжатый газ, у которого нет причин двигаться со скоростью большей скорости звука, так как движение частиц хаотично и всегда найдутся частицы движущиеся в противоположную сторону. При этом совершенно неважно какое давление и какого размера будет дырка, это определяет лишь то, насколько близко подойдёт скорость потока к скорости звука при отсутствии сверхзвукового сопла. С контуром сопла это связано очень просто. Сужение - это лишь часть ёмкости, а ёмкость - это замкнутая поверхность. И пока есть замкнутость - есть и хаотичное движение частиц. Когда появляется дырка, замкнутость нарушается, но при подходе к дырке в сужении происходит банальный отскок молекул от стенок в противоположном направлении потоку. Разумееться поток имея скорость движения сметает противоположно движущиеся молекулы, увлекая их за собой. При отсутствии сверхзвукового сопла, газ не достигает скорости звука в минимальном сечении, а лишь стремиться к нему ( иначе бы ветер должен дуть как минимум со скоростью звука всегда). Та часть потока, которая соответсвует свободному сечению, равной площади дырки, также не разгонится больше скорости звука, так как для этого нужно давление большее, чем существующее в ёмкости. Дырка в ёмкости, находящейся под давлением приводит к неравновесному состоянию этой ёмкости, появляется нескомпенсированное давление. Тогда газ должен мгновенно исчезнуть, а вместе с ним и давление. Но мгновенно ничего в природе не происходит, поэтому газ ускоряется, а на ускорение нужно приложить силу, а сила эта не может превысить давление в ёмкости. По распределению Максвела, средняя скорость - это усредненная скорость одной молекулы. Скорость звука точно описывает скорость распространения молекул в одном направлении, с учётом их степеней свободы движения, так как процесс распространения звуковых колебаний принято считать адиабатным. Поэтому скорость звука несколько меньше получается средней скорости движения молекул.
иначе бы ветер должен дуть как минимум со скоростью звука всегда). Та часть потока, которая соответсвует свободному сечению, равной площади дырки, также не разгонится больше скорости звука, так как для этого нужно давление большее, чем существующее в ёмкости. Дырка в ёмкости, находящейся под давлением приводит к неравновесному состоянию этой ёмкости, появляется нескомпенсированное давление. Тогда газ должен мгновенно исчезнуть, а вместе с ним и давление. Но мгновенно ничего в природе не происходит, поэтому газ ускоряется, а на ускорение нужно приложить силу, а сила эта не может превысить давление в ёмкости. По распределению Максвела, средняя скорость - это усредненная скорость одной молекулы. Скорость звука точно описывает скорость распространения молекул в одном направлении, с учётом их степеней свободы движения, так как процесс распространения звуковых колебаний принято считать адиабатным. Поэтому скорость звука несколько меньше получается средней скорости движения молекул.
При установке сверхзвукового сопла поток газа преодолевает скорость звука в минимальном сечении и продолжает ускоряться. Почему именно в минимальном не после? Отскок молекул от стенок сверхзвукового сопла совпадает с общим направлением потока, поэтому нет ничего, чтобы могло распространять звуковые волны против течения, а наоборот это приводит к всё более возрастающей скорости потока.
kirya> Есть ли где-нибудь упрощенная методика расчета формы сопла?
Есть - методика последовательного приближения и поиска.
Ну попытаюсь объяснить. Скорость звука описывает термодинамическое состояние газа. Чем больше внутренняя энергия газа и чем меньше его молекулярный вес, тем больше будет скорость звука. А скорость звука обусловлена хаотичным движением молекул, так вот если газ не расширяется, то как он может разогнаться быстрее скорости звука или, что тоже самое, потратить больше энергии чем в нём есть. То, что нужно сужать - это просто закон бернулли, в данном случае одинаково справедлив для всего, что течёт.
kirya> Формулы которые там приведены дают объяснение, но самой сути процесса я не понимаю. Что мешает газу разгоняться до сверхзвуковой скорости в сужающемся канале?
А мешает ему в этом закон распределения Максвела. Молекулы движуться хаотично, и есть, которые движуться с максимальной скоростью и есть те, которые вообще не движуться. Поэтому есть среднее значение скорости газа. Однако газ в замкнутом пространстве не вдижется. При появлении дырки с перепадом давлений, газ начинается ускоряться, появляется течение. А при подходе к минимальному сечению в канале, молекулы начинают двигаться примерно в одном направлении, но ещё очень значительно число молекул движущихся в противоположном направлении потоку. Что означает возможность передачи звуковых колебаний от дырки внутрь камеры.
Короче молекулы при подходе к минимальному сечению, движуться во всех направлениях, а после они уже не могут двигаться против потока. При этом их перпендикулярные оси движения скорости падают, и молекулы движуться преимущественно в одном направлении приближаясь к макисмально возможной скорости, определяемой внутренней энергией газа.
Понимать это надо так, что всё до дырки - это сжатый газ, у которого нет причин двигаться со скоростью большей скорости звука, так как движение частиц хаотично и всегда найдутся частицы движущиеся в противоположную сторону. При этом совершенно неважно какое давление и какого размера будет дырка, это определяет лишь то, насколько близко подойдёт скорость потока к скорости звука при отсутствии сверхзвукового сопла. С контуром сопла это связано очень просто. Сужение - это лишь часть ёмкости, а ёмкость - это замкнутая поверхность. И пока есть замкнутость - есть и хаотичное движение частиц. Когда появляется дырка, замкнутость нарушается, но при подходе к дырке в сужении происходит банальный отскок молекул от стенок в противоположном направлении потоку. Разумееться поток имея скорость движения сметает противоположно движущиеся молекулы, увлекая их за собой. При отсутствии сверхзвукового сопла, газ не достигает скорости звука в минимальном сечении, а лишь стремиться к нему (
 иначе бы ветер должен дуть как минимум со скоростью звука всегда). Та часть потока, которая соответсвует свободному сечению, равной площади дырки, также не разгонится больше скорости звука, так как для этого нужно давление большее, чем существующее в ёмкости. Дырка в ёмкости, находящейся под давлением приводит к неравновесному состоянию этой ёмкости, появляется нескомпенсированное давление. Тогда газ должен мгновенно исчезнуть, а вместе с ним и давление. Но мгновенно ничего в природе не происходит, поэтому газ ускоряется, а на ускорение нужно приложить силу, а сила эта не может превысить давление в ёмкости. По распределению Максвела, средняя скорость - это усредненная скорость одной молекулы. Скорость звука точно описывает скорость распространения молекул в одном направлении, с учётом их степеней свободы движения, так как процесс распространения звуковых колебаний принято считать адиабатным. Поэтому скорость звука несколько меньше получается средней скорости движения молекул.
иначе бы ветер должен дуть как минимум со скоростью звука всегда). Та часть потока, которая соответсвует свободному сечению, равной площади дырки, также не разгонится больше скорости звука, так как для этого нужно давление большее, чем существующее в ёмкости. Дырка в ёмкости, находящейся под давлением приводит к неравновесному состоянию этой ёмкости, появляется нескомпенсированное давление. Тогда газ должен мгновенно исчезнуть, а вместе с ним и давление. Но мгновенно ничего в природе не происходит, поэтому газ ускоряется, а на ускорение нужно приложить силу, а сила эта не может превысить давление в ёмкости. По распределению Максвела, средняя скорость - это усредненная скорость одной молекулы. Скорость звука точно описывает скорость распространения молекул в одном направлении, с учётом их степеней свободы движения, так как процесс распространения звуковых колебаний принято считать адиабатным. Поэтому скорость звука несколько меньше получается средней скорости движения молекул.При установке сверхзвукового сопла поток газа преодолевает скорость звука в минимальном сечении и продолжает ускоряться. Почему именно в минимальном не после? Отскок молекул от стенок сверхзвукового сопла совпадает с общим направлением потока, поэтому нет ничего, чтобы могло распространять звуковые волны против течения, а наоборот это приводит к всё более возрастающей скорости потока.
kirya> Есть ли где-нибудь упрощенная методика расчета формы сопла?
Есть - методика последовательного приближения и поиска.
PAL
втянувшийся
kirya> Есть ли где-нибудь упрощенная методика расчета формы сопла?
Все очень просто: вводишь в любом поисковике фразу расчет сопла Лаваля и тебе выбрасывает кучу ссылок по методикам такого расчета, например одна из них: XuMuK.ru - Критическое давление и скорость. Сопло Лаваля. «ТЕПЛОТЕХНИКА. КУРС ЛЕКЦИЙ», Скрябин В.И
Все очень просто: вводишь в любом поисковике фразу расчет сопла Лаваля и тебе выбрасывает кучу ссылок по методикам такого расчета, например одна из них: XuMuK.ru - Критическое давление и скорость. Сопло Лаваля. «ТЕПЛОТЕХНИКА. КУРС ЛЕКЦИЙ», Скрябин В.И
PAL
втянувшийся
Узнал про свою трубу (внешний диаметр 60 мм, толщина стенки 3 мм) новые данные из интернета, а именно: 1. Алюминий марки АД 31
2. Предел прочности (сигма временная) – 15-22 кгс/мм.кв
3. Предел текучести (сигма текучести) – 7-12 кгс/мм.кв18-20
4. Относительное удлинение – 8-15 %
5. Модуль упругости - 7100 кгс/мм.кв.
6. Плотность p - 32,71 г/см
7. Теплопроводность (лямбда) - 188Вт/(м* С)
8. Коэффициент линейного расширения а, - К-1х10 6
9. Твердость НВ - 78,6
еще данные:
Плотность, г/см3 - 2,7
Прочность, МПа - 150-250
Модуль Юнга, МПа - 70000
Электропроводность, МСм/м - 30
Теплопроводность, Вт/м • град - 140
Звукопроводность, Дб/см - 50
Специфические свойства - хороший проводник
Я совсем не разбираюсь в свойствах металлов, поэтому, Вопрос в следующем: хочется, чтобы рабочее давление в двигателе из оной трубы было 6-7 МПа, да еще 3-4 МПа про запас, итого 10 МПа, как рассчитать, выдержит такая труба 10Мпа в течении 2 сек. горения топлива или нет?
2. Предел прочности (сигма временная) – 15-22 кгс/мм.кв
3. Предел текучести (сигма текучести) – 7-12 кгс/мм.кв18-20
4. Относительное удлинение – 8-15 %
5. Модуль упругости - 7100 кгс/мм.кв.
6. Плотность p - 32,71 г/см
7. Теплопроводность (лямбда) - 188Вт/(м* С)
8. Коэффициент линейного расширения а, - К-1х10 6
9. Твердость НВ - 78,6
еще данные:
Плотность, г/см3 - 2,7
Прочность, МПа - 150-250
Модуль Юнга, МПа - 70000
Электропроводность, МСм/м - 30
Теплопроводность, Вт/м • град - 140
Звукопроводность, Дб/см - 50
Специфические свойства - хороший проводник
Я совсем не разбираюсь в свойствах металлов, поэтому, Вопрос в следующем: хочется, чтобы рабочее давление в двигателе из оной трубы было 6-7 МПа, да еще 3-4 МПа про запас, итого 10 МПа, как рассчитать, выдержит такая труба 10Мпа в течении 2 сек. горения топлива или нет?
> 6. Плотность p - 32,71 г/см
какая-то странная цифра, не похоже на плотность алюминия.
Прочность, МПа - 150-250
Модуль Юнга, МПа - 70000
По этим данным очень похоже на сплав 6061-T4 drawn tubing из программы casing.
Расчёт в этой программе даёт рабочее давление до 110 атм, разрыв при 213 атм.
какая-то странная цифра, не похоже на плотность алюминия.
Прочность, МПа - 150-250
Модуль Юнга, МПа - 70000
По этим данным очень похоже на сплав 6061-T4 drawn tubing из программы casing.
Расчёт в этой программе даёт рабочее давление до 110 атм, разрыв при 213 атм.
Serge77> Прочность, МПа - 150-250
Serge77> Модуль Юнга, МПа - 70000
Serge77> По этим данным очень похоже на сплав 6061-T4 drawn tubing из программы casing.
Serge77> Расчёт в этой программе даёт рабочее давление до 110 атм, разрыв при 213 атм.
Ой ой ой! Не путайте "Прочность, МПа" оно-же "Предел прочности (сигма временная)" и "Предел текучести (сигма текучести)". Нам нужно брать именно второе (которое поменьше).
Ну и закладывайте запас прочности всегда! Даже самолеты (как конструкции с наименьшим запасом) имеют коэффициенты запаса не менее 1.5. А такие конструкции как лифты могут иметь коэфф запаса до 10!
Так что 2-ку накиньте на кривости наколенной технологии и скачки давления в камере.
Итого получаем допускаемое давление (рабочее) до 67 атм. Вполне пригодно.
Только стоит учесть что нельзя допускать нагрева выше 100 С, алюминиевые сплавы быстро теряют прочность.
Serge77> Модуль Юнга, МПа - 70000
Serge77> По этим данным очень похоже на сплав 6061-T4 drawn tubing из программы casing.
Serge77> Расчёт в этой программе даёт рабочее давление до 110 атм, разрыв при 213 атм.
Ой ой ой! Не путайте "Прочность, МПа" оно-же "Предел прочности (сигма временная)" и "Предел текучести (сигма текучести)". Нам нужно брать именно второе (которое поменьше).
Ну и закладывайте запас прочности всегда! Даже самолеты (как конструкции с наименьшим запасом) имеют коэффициенты запаса не менее 1.5. А такие конструкции как лифты могут иметь коэфф запаса до 10!
Так что 2-ку накиньте на кривости наколенной технологии и скачки давления в камере.
Итого получаем допускаемое давление (рабочее) до 67 атм. Вполне пригодно.
Только стоит учесть что нельзя допускать нагрева выше 100 С, алюминиевые сплавы быстро теряют прочность.
У меня для "холодной" трубы D=60мм S=3мм получилось максимум 9МПа. Формулы и описание в "rar". Это по "нашим" формулам, мы водоводы высокого давления на остаточную толщину считаем.
Прикреплённые файлы:
Простите,-спросили Мартовского Кота,-действительно ли в марте месяце? Какая чушь,- ответил Мартовский Кот,- и март месяц не исключение! http://martkot.embedders.org
timochka> Ой ой ой! Не путайте "Прочность, МПа" оно-же "Предел прочности (сигма временная)" и "Предел текучести (сигма текучести)". Нам нужно брать именно второе (которое поменьше).
Так я и брал то, что поменьше. Для 6061-T4 drawn tubing поменьше - 110 МПа, а побольше - 207 МПа. Это самое "побольше" как раз вписывается в заданные "Прочность, МПа - 150-250". Рабочее давление - это посчитанное из "поменьше", а разрыв - из "побольше". Вроде всё правильно.
timochka> Ну и закладывайте запас прочности всегда!
Обязательно.
Так я и брал то, что поменьше. Для 6061-T4 drawn tubing поменьше - 110 МПа, а побольше - 207 МПа. Это самое "побольше" как раз вписывается в заданные "Прочность, МПа - 150-250". Рабочее давление - это посчитанное из "поменьше", а разрыв - из "побольше". Вроде всё правильно.
timochka> Ну и закладывайте запас прочности всегда!
Обязательно.
MartKot> У меня для "холодной" трубы D=60мм S=3мм получилось максимум 9МПа. Формулы и описание в "rar". Это по "нашим" формулам, мы водоводы высокого давления на остаточную толщину считаем.
Т.е. 90 атм - все верно. У вас коэфф запаса другие, и формула для "толстой" трубы похоже.
Для стали запас берут поменьше, для алюминия побольше.
Т.е. 90 атм - все верно. У вас коэфф запаса другие, и формула для "толстой" трубы похоже.
Для стали запас берут поменьше, для алюминия побольше.
PAL
втянувшийся
Супер, спасибо всем! Теперь хоть что-то прояснилось по данным.
У меня 4 сопла 5, 6, 7 и 8 МПа, (на 8 МПа я «лапухнулся», хотел сделать на 4МПа, не ту цифру в чертеже поставил) начнем испытания с 6-ти МПа, а там посмотрим на 5-ть или на 7-мь ставить при следующем испытании. Хотя особо не разгонишься, на 1 испытание 1,5 кг. топлива нужно... Теперь уделю время размышлениям о теплоизоляции.
У меня 4 сопла 5, 6, 7 и 8 МПа, (на 8 МПа я «лапухнулся», хотел сделать на 4МПа, не ту цифру в чертеже поставил) начнем испытания с 6-ти МПа, а там посмотрим на 5-ть или на 7-мь ставить при следующем испытании. Хотя особо не разгонишься, на 1 испытание 1,5 кг. топлива нужно... Теперь уделю время размышлениям о теплоизоляции.
Имеет ли смысл делать вот такие вот фаски (или даже сглаживание сопряжением поверхностей дугой окружности). Уменьшатся ли тепловая и механическая нагрузки на критику, как повлияет на разгар? Уменьшится ли сопротивление потоку продуктов сгорания?
Прикреплённые файлы:
Lioxa
втянувшийся
У меня на двиателе ~900гр топлива эти уголки унесло, после одного испытания.
Правда на двигателях поменьше 100-200гр сопло выдерживало по несколько десятков пусков без всякой корозии.
Правда на двигателях поменьше 100-200гр сопло выдерживало по несколько десятков пусков без всякой корозии.
Lioxa> У меня на двиателе ~900гр топлива эти уголки унесло, после одного испытания.
У тебя на сайте есть чертёж этого сопла? Можешь дать ссылку?
У тебя на сайте есть чертёж этого сопла? Можешь дать ссылку?
Copyright © Balancer 1997..2018
Создано 19.10.2007
Связь с владельцами и администрацией сайта: anonisimov@gmail.com, rwasp1957@yandex.ru и admin@balancer.ru.
Создано 19.10.2007
Связь с владельцами и администрацией сайта: anonisimov@gmail.com, rwasp1957@yandex.ru и admin@balancer.ru.
/11-web.jpg)
 Serge77
Serge77

 инфо
инфо инструменты
инструменты SashaPro
SashaPro








 Lioxa
Lioxa