Использование твердотельных гироскопов в ракетомоделях

SashaMaks> О, я так и думал

Ты до сих пор не извинился.
Писанина твоя мне не интересна.

Massaraksh> Ну, я заодно и пытаюсь понять алгоритм определения текущей координаты объекта в зависимости от показаний "полноценной системы инерциальных датчиков".

У меня почти написана прога для МК.
Полностью написано получение направляющих косинусов из данных гироскопов.
На стр. 13 этой темы есть намёки.

Я всё считаю в абсолютной системе координат с центром в центре Земли (Земля = пуп Вселенной).
Система не вращается с Землёй, ось Z направлена на северный полюс, X — на весеннее равноденствие, Y — на 90 градусов от X, знак не помню.

Вот ракета стоит на старте — на расстоянии 6 тысяч км от начала координат, а её оси наклонены под большими углами к осям системы, и она движется со скоростью 400 м/с вместе с поверхностью Земли.

Для определения ориентации ракеты я не использую углы, а использую направляющие косинусы.
(см. например: Направляющие косинусы вектора.)
Это позволяет не нагружать МК вычислениями тригонометрических функций.

Направление каждой из трёх осей ракеты задаётся тремя косинусами.
Итого, получается 9 величин.
Это, вообще-то, сильно избыточно. Но зато есть удобство.

Из показаний гироскопов я как раз получаю изменение этих 9 косинусов (cosX_x и другие восемь).

Чтоб получить ускорение в абсолютной системе, я беру показания акселерометра x и умножаю на три косинуса оси x. И получаю "кусочки" компонентов ускорения в абсолютной системе:

aX_x = ax * cosX_x
aY_x = ax * cosY_x
aZ_x = ax * cosZ_x

Аналогично для акселорометров y и z: aX_y, aY_y, aZ_y, aX_z, aY_z, aZ_z.
Складываю "кусочки" и получаю компоненты ускорения в абсолютной системе (с учётом поля тяжести, конечно):

aX = aX_x + aX_y + aX_z - gX
aY = aY_x + aY_y + aY_z - gY
aZ = aZ_x + aZ_y + aZ_z - gZ

Девять умножений, девять сложений, никакой тригонометрии.

Дальше примитивное интегрирование в абсолютной системе:
вектор скорости: v = v + a * dt
вектор координат: r = r + v * dt

Всё.

Xan>...
Спасибо, попробую построить модель.

Xan> Несколько раз уже читал про "датчики в центре масс".
Xan> И все эти несколько раз не могу понять — зачем?!

Для облегчения жизни, в смысле, математики, при нежёсткой ракете и неидеальных датчиках.

Xan> Ну вот к ракете приделана палка вбок, на конце палки — датчики.
Xan> Ракета вращается вокруг оси и вообще летит криво.

ну представь, что акселерометр бокового ускорения имеет очень маленький гистерезис, т.е. его показания при смене знака ускорения чуть-чуть зависят от предыдущих показаний. А это реалистичная картина.

Xan> Как всё это помешает определить положение датчиков?
Xan> Причём здесь центр масс?

Если, допустим, мы не знаем точно частоту собственных колебаний ракеты, как упругого стержня (а у жидкостной ракеты она меняется по мере выработки топлива), а датчик стоит далеко от центра масс, мы не сможем вычленить собственные колебания ракеты и автоколебания, создаваемые системой управления.

Xan> Всё.
Построил модель, на плоскости твои формулы, вроде бы, работают. Теперь хочу проверить на реальном приборе.
Вопрос тебе: гироскоп выдает направляющие косинусы?
И вопрос тебе и Андрею: какой чип посоветуете купить (3-осевой гироскоп + 3-осевой акселерометр) для этих целей, но без фанатизма (очень большая точность мне не нужна)?

Massaraksh> Вопрос тебе: гироскоп выдает направляющие косинусы?

Нет, только угловые скорости, причём, вокруг ТЕКУЩИХ осей. Надо интегрировать.

Massaraksh> И вопрос тебе и Андрею: какой чип посоветуете купить (3-осевой гироскоп + 3-осевой акселерометр) для этих целей, но без фанатизма (очень большая точность мне не нужна)?
Что-нибудь типа этого:

Там до кучи и магнитометр и барометр стоят.

Б.г.>...
Ага, спасибо.

Massaraksh> Вопрос тебе: гироскоп выдает направляющие косинусы?

Решил причесать текст и дополнить интегрированием скорости и координат.
И комментариев понавставлял. А то склероз так и нападает!

Пока получился черновик, не пропущенный через компилятор и железо.
Так что ошибки там могут быть самые разные.
Но подумал, что лучше раньше показать, а то наладка может отложиться в долгий ящик.

(https://dl.dropboxusercontent.com/u/.../Inertial_math_2015.06.20.txt)

Там ещё гравитация эллиптической Земли не вставлена.

Думал насчёт точности, какую надо применить в этой арифметике.
Ну, чтоб облегчить жизнь для МК.
Получилось, что вращение не имеет смысла считать точнее, чем float.
А вот для космических скоростей и координат точности float сильно не хватает.
Пытался всяко применить числа с фиксированной точкой, у них мантисса длиннее, чем у плавающих. Но всё равно мало и надо извращаться, чтоб over/under-flow не случилось.
Решил, что ресурсы человеческого разума надо беречь, а лучше МК надо заставить считать double. Ему всё равно в полёте, когда он из рук хозяина вырвется, делать будет нечего!

Xan> Решил причесать текст и дополнить интегрированием скорости и координат.

1. VX += AX * dt;    X += VX * dt;                         // Интегрируем вектор скорости
2. VY += AY * dt;    Y += VY * dt;                         // и координат.
3. VZ += AZ * dt;    Z += VZ * dt;

Трапециями или Симпсоном будет точнее, чем прямоугольниками. Мне кажется, здесь это достаточно критично. Хотя, конечно, это надо проверять на реальных примерах.

Massaraksh> Трапециями или Симпсоном будет точнее, чем прямоугольниками.

Ну, основа для размышлений должна быть простая и понятная.
А потом уже можно совершенствовать.

Massaraksh> Трапециями или Симпсоном будет точнее, чем прямоугольниками.
Не знаю, как насчёт координат, а для углов я прикинул.
Разница между методом прямоугольников и трапеций тем больше, чем быстрее меняется подынтегральная функция.
У меня в тестовой программе разворот по тангажу занимает 180 секунд.
Для периода в 1/409,6 секунды и величиной кванта угловой скорости 1/160 градуса в секунду разница между прямоугольниками и трапециями за всё время разворота составит не более 0,56 градуса. При том, что сам датчик за эти 180 секунд уйдёт градуса на полтора.

Текст пропустил через компилятор в железо.
Исправил старые ошибки, добавил новые!!!

По старой ссылке теперь лежит обновлённый файл:
(https://dl.dropboxusercontent.com/u/.../Inertial_math_2015.06.20.txt)

Результаты проверки быстродействия на железе:

Все переменные float — 238 вычислений в секунду
Скорость и координаты double — 194 — в 1.23 раза тормозит
Все переменные double — 120 — а это в два раза, но это и не интересно

Это при генераторе 12.8 МГц и специально заторможенном студенческом (free) компиляторе XC16(v1.11).
Total program memory used (bytes): 0x1761 (5985) 18%
Total data memory used (bytes): 0x12a (298) 14%

Можно частоту поднять до 32 МГц и компилятор применить сорта "про".

Частоту менять не хочется, к ней UART привязан. А генератор уже куплен.
Придётся включать "про" в компиляторе.
И, наверное, тормозить датчики с 400 до 200 отсчётов в секунду. Или даже до 100.

Б.г.> Разница между методом прямоугольников и трапеций тем больше, чем быстрее меняется подынтегральная функция.
Б.г.> У меня в тестовой программе разворот по тангажу занимает 180 секунд.
Понятно. Но я пытаюсь в общем случае. К тому же, бывают нештатные ситуации.

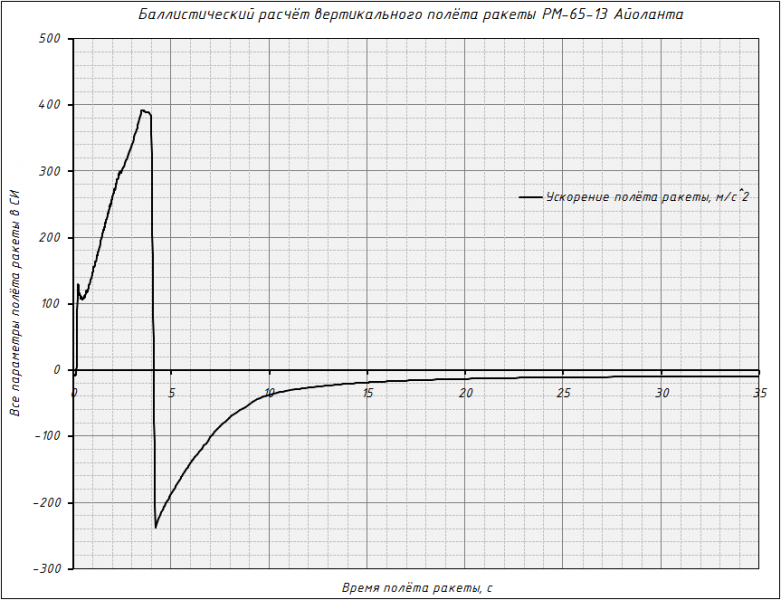
Massaraksh> Можешь нарисовать предполагаемый график показаний датчика ускорения на твоей виртуальной ракете?

Вот примерно такой и будет кривая ускорений с акселерометра по главной оси:

Xan> Ты до сих пор не извинился.

Для меня алогично извиняться перед человеком, который меня обвиняет и оскорбляет в несуществующих грехах вот уже 2,5 года.

Xan> Писанина твоя мне не интересна.

Писанина пока что у тебя тут, а у меня дело, за которым стоит практика и действительность.
У тебя даже код в программе не проверен на работоспособность в теории...

Xan>> Всё.
Massaraksh> Построил модель, на плоскости твои формулы, вроде бы, работают. Теперь хочу проверить на реальном приборе.

Это:
Xan: "aX_x = ax * cosX_x"
Xan: "aY_x = ax * cosY_x"
Xan: "aZ_x = ax * cosZ_x"
Xan: "aX = aX_x + aX_y + aX_z - gX"
Xan: "aY = aY_x + aY_y + aY_z - gY"
Xan: "aZ = aZ_x + aZ_y + aZ_z - gZ"

Не относится к любым объектам. И по математической сути вообще неправильно. Но, возможно, что в этом мире самодельной математики, свои условия на ошибки. Возможно это взаимосвязано, и поэтому так к ним щепетильно относятся, но я в это не вникал.

Xan> И, наверное, тормозить датчики с 400 до 200 отсчётов в секунду. Или даже до 100.

Печально.
А я помню твой алгоритм и тоже его прогнал на скорость в сравнении со своим универсальным. Быстрей он оказался всего лишь в 1,5 раза. А всё потому, что в универсальном (правильном) преобразовании координат очень хорошо оптимизируются уравнения с косинусами и синусами

SashaMaks> Для меня алогично извиняться

Лечись и извиняйся.


(Что-то я погорячился несколько.)

SashaMaks> Вот примерно такой и будет кривая ускорений с акселерометра по главной оси:
И в какой точке апогей?

Xan> (Что-то я погорячился несколько.)
Немножко да.

Massaraksh> И в какой точке апогей?

Так это:
SashaMaks: "4. Основным и достаточным условием определения момента прохождения ракетой апогея является минимум скорости её движения..."

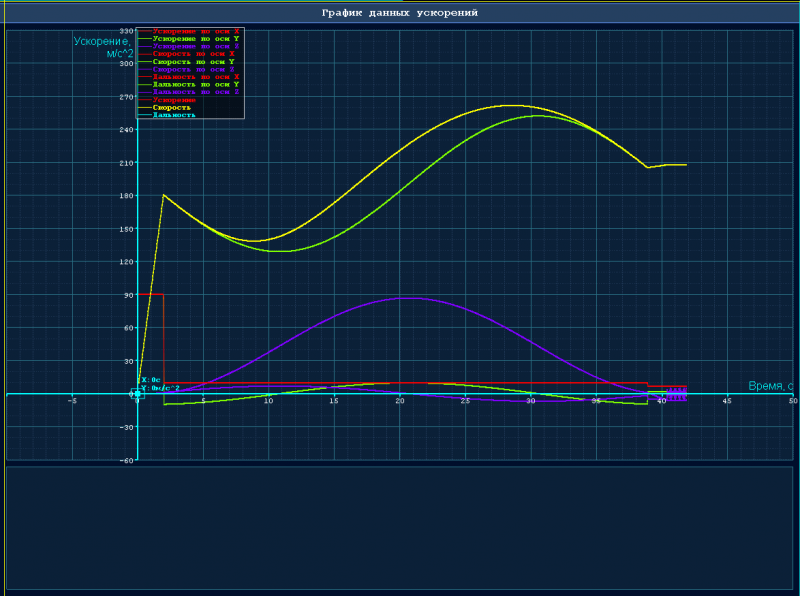
Вот график уже из 3-х мерного симулятора, где имитируются данные с датчиков. Но тут ракета другая, менее мощная, а минимум скорости всё равно есть.

SashaMaks>> Для меня алогично извиняться
Xan> Лечись и извиняйся.

Может ещё и диагноз мне озвучишь? А то я что-то не понял к какому мне доктору обратиться и с чем...

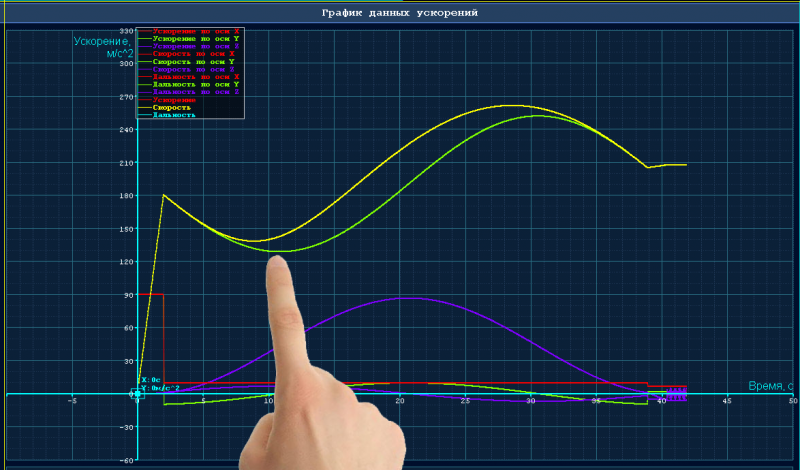
Massaraksh>> И в какой точке апогей?
SashaMaks> Так это:
Ты пальцем в график ткни.

Massaraksh> Ты пальцем в график ткни.

Я не про этот график.