Конструкция ракет XI

mihail66> Да.
mihail66> Для первой ракеты сделай площадь стабилизаторов побольше, и с возможностью их обрезки прямо на ракете.

RocKI> Загрузка балластом - дурной тон. Можешь собрать ракету, но стабилизаторы подобрать и приклеить в последний момент.

Я вас понял. Ну в теории тогда волноваться мне не о чем, вряд ли ЦД по обоим методам будет выше центра тяжести. Или нет?

feonor12> Я вас понял. Ну в теории тогда волноваться мне не о чем, вряд ли ЦД по обоим методам будет выше центра тяжести. Или нет?

Я тебя не понял. Все зависит от тебя, где ты организуешь все эти центры. А насчет ЦАП, еще раз повторю, это для экстремальных режимов очень больших углов атаки. Он нужен только для редких случаев, когда такие углы могут возникнуть. Если у вас руки не кривые и ракеты не экзотические, то не берите его в голову, используйте при проектировании только ЦДБ.

RocKI> Я тебя не понял. Все зависит от тебя, где ты организуешь все эти центры.

Теперь я не понял. В смысле, организую? Есть чертеж, по которому строится планер. И расчет. Я либо не до конца понимаю, что такое центр давления, раз не понимаю как его организовать, либо да.

RocKI> Забей на ЦАП, ориентируйся по Барроуману.
Да, возможно ты прав. Единственная причина отказа от ЦДБ то, что второй ступени с полной массой и не включенным двигателем придется "мертвой" лететь по инерции около 2.5 км. А "оживет" она на маленькой скорости.
Вот и хочется, чтобы во время инерционного полета ее ЦД (как центр проекции) находился рядом с ЦТ.

feonor12> Теперь я не понял. В смысле, организую? Есть чертеж, по которому строится планер. И расчет. Я либо не до конца понимаю, что такое центр давления, раз не понимаю как его организовать, либо да.
RocKI имел ввиду, что положение ЦД зависит от площади стабов, а площадь стабов зависит от тебя.
Вот как ты организуешь, так и будет.
feonor12> Центр тяжести, очевидно, не может быть ниже, ведь двигатель длиннее точки ЦД...
Всякое бывает, но это легко проверяется веревкой.
*А если соберешься ее на веревке крутить, и у ракеты предусмотрено разделение посередине, то прими меры чтобы она не сломалась пополам. Например на место стыковки временно накрути несколько витков электрокартона и зафиксируй скотчем (сделай длинную соединительную муфту).

feonor12> Центр давления, по классическому расчету, в моем случае у границ стабилизаторов. Центр тяжести, очевидно, не может быть ниже, ведь двигатель длиннее точки ЦД. А там еще авионика, система спасения.

Ну вот видишь, ты уже и организовываешь. А если серьезно, то без стабов ЦД находится на ГО, с большим стабом -у основания стабов. Значит есть размеры стабилизатора, при которых ЦД может находится между этими точками. Т.е. все зависит от подбора площади стабилизаторов.
А если совсем серьезно, то из практики площадь стабов можно взять с запасом. "Лишняя" аэродинамическая устойчивость для наших ракет не большая проблема. Только надо не забывать, что переразмеренный стабилизатор это тоже лишний вес. Да и смотрится не очень.

feonor12> ....вряд ли ЦД по обоим методам будет выше центра тяжести. Или нет?
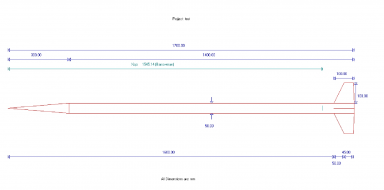
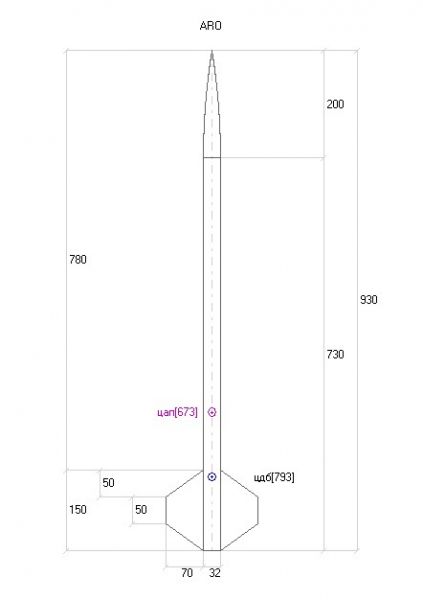
А вот вопрос к прикрепленной картинке.
Из каких соображений выбрана длинна корпуса?
Не многовато ли 930мм для диаметра 32мм?

RocKI> На малых углах атаки, и это доказано Барроуманом, цилиндрическая часть ракеты не влияет на положение ЦД. Таким образом положение ЦД зависит только от размеров и формы ГО.
RocKI> А если серьезно, то без стабов ЦД находится на ГО

Где доказательства?

feonor12> Ну в теории тогда волноваться мне не о чем, вряд ли ЦД по обоим методам будет выше центра тяжести. Или нет?

Для этого нужно посчитать ЦМ (центр масс). Можно вручную, можно в CAD программах.

mihail66> Допустим ты уже знаешь отклонение вектора, горизонтальную скорость и разряжение.
mihail66> Какие действия для правильного неуправляемого полета предпринимать?

Делать так, чтобы не выходить за установленные пределы. Это достигается надёжностью и воспроизводимостью собираемых изделий. А расчёт этих пределов действительно большой.

RocKI> Нормальная ракета при нормальных условиях пуска никогда не выходит на большие углы атаки.

Скорость бокового ветра 8 м/с;
Скорость схода ракеты с направляющих 20 м/с;
Угол атаки 21,8°;

Скорость бокового ветра 8 м/с;
Скорость схода ракеты с направляющих 10 м/с;
Угол атаки 38,7°.

Наверное - это маленькие углы атаки...

mihail66> Не многовато ли 930мм для диаметра 32мм?

из соображений, что бы все влезло. Двигатель 275 мм, БРЭО 180 мм, мортирка около 50 мм, уже пол метра. А дальше соединительная втулка 40, поршень 40, сантиметра 3 на стыковку с ГО и остается 115 на парашют, по идее все пространство фюзеляжа будет занято. Ну ГО можно покороче сделать, мне просто 200 мм понравилось визуально.

feonor12> из соображений, что бы все влезло.

Понятно, у меня влезало в 650мм.
(правда не бумаге)
Собственно длинный корпус тебе помог поднять ЦТ на ЦД.
Но длинный корпус увеличит АД сопротивление.
А в какой программе было рассчитано расположение центров?

SashaMaks> Для этого нужно посчитать ЦМ (центр масс). Можно вручную, можно в CAD программах.
А на веревке не проще? Для ракет ЦМ совпадает с ЦТ.

mihail66> Собственно длинный корпус тебе помог поднять ЦТ на ЦД.

Не помог. Удлинение корпуса L/D не увеличивает запаса аэродинамической устойчивости.

SashaMaks>> Для этого нужно посчитать ЦМ (центр масс). Можно вручную, можно в CAD программах.
mihail66> А на веревке не проще? Для ракет ЦМ совпадает с ЦТ.

Проще!
Вчера вырубился, не успел проверить)))
Сегодня обязательно проверю!
Опыт ерундовый: бумажная трубка с двумя заглушками из АБС пластика, одна плоская, другая конус. Вот и увидим, где же находится ЦД без стабилизаторов...

mihail66>> Собственно длинный корпус тебе помог поднять ЦТ на ЦД.
SashaMaks> Не помог. Удлинение корпуса L/D не увеличивает запаса аэродинамической устойчивости.

Это от чего же?
Удлинение корпуса, в разумных пределах, увеличивает расстояние от ЦТ до ЦД (конечно если при этом смещается масса в сторону ГО).
Можно придумать вариант где это не произойдет, но этот вариант будет каким-то "НЕракетомедельным".

mihail66>> А на веревке не проще? Для ракет ЦМ совпадает с ЦТ.
SashaMaks> Проще!
Это ты для запуска "палки"?
Очень интересно!!!

mihail66> Это от чего же?

Потому что, диаметр цилиндрической части корпуса не участвует в определении запаса аэродинамической устойчивости ЛА. Только продольные размеры.

mihail66> Удлинение корпуса, в разумных пределах, увеличивает расстояние от ЦТ до ЦД (конечно если при этом смещается масса в сторону ГО).

Само по себе увеличение длины ЛА, как его габарита, запаса аэродинамической устойчивости не повышает, так как это величина относительная, и относительна она этой самой длины ЛА.

По определению из учебников по аэродинамике (Конструкция ракет XI [SashaMaks#15.05.16 08:52]) запас аэродинамической устойчивости будет:

S[%] = 100[%] * (ЦД[мм] - ЦМ[мм]) / L[мм], где:
ЦД[мм] - Координата центра давления ЛА от носа;
ЦМ[мм] - Координата центра масс ЛА от носа;
L[мм] - Длина ЛА.

Запас устойчивости в диаметрах корпуса или его калибрах вводит в опасное заблуждение о том, что при уменьшении диаметра корпуса, запас будет увеличиваться!

В сравнении на запасы чего либо участвует две величины:
1. Фиксированная [S2];
2. Сравниваемая S1.

Для фиксированной величины обычно задан константный предел, например запас прочности [S2] равен 2 для конструкций летательных аппаратов или сосудов, работающих под давлением.

С этой величиной сравнивается ещё одна величина, которая переменная и зависит от расчёта или практического измерения.

Для удовлетворения неравенства вида S1 > [S2] можно пойти двумя путями или понизить предел S2 или повысить величину S1. Ошибочная формула с единицами в [диаметрах], как раз даёт такую возможность, но в относительных величинах ничего не изменяется. В этом и ошибочность применения неправильной размерности в запасах.

Можно пересчитать величину [S2] в диаметры, но тогда рекомендуемый константный предел будет совсем не константным и будет зависит от конкретной ракеты и её формы в каждом конкретном случае - потеряет свою универсальность, и его нельзя будет применять к разным ракетам. Т.е. у одной ракеты будет достаточно запаса в 2D, у другой в 4D, а у третьей в 6D и зависеть это будет во многом от соотношения L/D, которое проще сократить для обоих величин и больше никогда на этом не заморачиваться.

SashaMaks> Запас устойчивости в диаметрах корпуса или его калибрах вводит в опасное заблуждение о том, что при уменьшении диаметра корпуса, запас будет увеличиваться!

Пример!

1. Рекомендация по запасу аэродинамической устойчивости: минимальный запас аэродинамической устойчивости равен 2D или 10% соответственно;

2. У проектируемой ракеты получился запас аэродинамической устойчивости 1D или 5% соответственно;

3. Ракету перепроектировали и увеличили ей L/D в два раза, т.е. фактически просто уменьшили диаметр корпуса в 2 раза;

4. У проектируемой ракеты получился запас аэродинамической устойчивости 2D или 5% уже не соответственно.

5. Выводы: 2D >= [2D] - устойчиво, а 5% < [10%] - неустойчиво, как и было.

С выводом 2D >= [2D] человек делает ракету, думая, что всё хорошо, запускает, а она улетает за бугор.

А с выводом 5% < [10%] её необходимо перепроектировать и причём совсем по-другому!

mihail66> А в какой программе было рассчитано расположение центров?

Rocki-design

SashaMaks> 3. Ракету перепроектировали и увеличили ей L/D в два раза, т.е. фактически просто уменьшили диаметр корпуса в 2 раза;
Ну если ты проводишь аналогию увеличения длины с уменьшением диаметра, пусть будет так.
Смотри на картинки.
Как при этом переместится ЦДБ, при неизменном ЦТ.

mihail66> Смотри на картинки.
А вот так переместится ЦАП.

SashaMaks>Запас устойчивости в диаметрах корпуса или его калибрах вводит в опасное заблуждение о том, что при уменьшении диаметра корпуса, запас будет увеличиваться!
Опасное заблуждение?

mihail66>> Смотри на картинки.
mihail66> Опасное заблуждение?

И ты действительно веришь в то, что именно в то количество раз [диаметров] увеличивается запас устойчивости?

Вот стоит только хотя бы на миг, хотя бы на раз отойти от деталей, так именно в детали и ткнут носом.

Вот смотри детальный расчёт:
(Конструкция ракет XI [SashaMaks#15.05.16 15:06])

Тут все (почти все) "блохи" учтены.