Как снимали лунную аферу...

aФон> Я же не спорю, я проясняю, в этом мой интерес (все эти т.н. "споры" - это чтобы игра была убедительней)
aФон> Я считаю, что мы очень ВАЖНЫЕ моменты прояснили.

Даже не представляешь. Мы доказали, что схема на твоем сайте с павильоном-туфта, сам ты ни хрена не понимаешь в кинопроизводстве, и при этом ловишь Коновалова и Якубовича на лжи. Это просто праздник.

Ос>> Ее уже выложил Юрий Красильников, отчего у Афона случилось баттхертио.
Лунит> Однако Юрий Красильников с некоторого момента оставляет без внимания просьбы Афона об уточняющих комментариях, таких как исходники и использованные опорные точки.

Судя по точности обработки от его поделки:

Оптимизация завершена .
Результаты:
среднее расстояние между точками: 0,657446
стандартное отклонение: 0,399036
максимум: 1,429149

Как снимали лунную аферу... [Yuri Krasilnikov#02.02.19 23:51]

\ Y.K.>> Вот, любуйся. … Не ори попусту. Hugin говорит, что совмещение неплохое. Оптимизация завершена . Результаты: среднее расстояние между точками: 0,657446 стандартное отклонение: 0,399036 максимум: 1,429149   Вот индикатор совмещения:   // Лунные космические программы

 

 

То кроме фокуса 18 мм (вместо 10 мм), он еще и точки очень ГРУБО ЗАДАВАЛ

Точность задания не должна быть хуже 0.3, а у него там аж максимум 1.43 присутствует, при таком подходе можно что угодно получить, но шавки типа Хэла будут подбрехивать и подвизгивать, они же один фиг нихрена не понимают.

Hal> Ну так теперь ты понял что софт выбрал не те точки? Или будешь дальше упираться как баран в своей тупости?

Оно что, спрашивает у софта, какие точки выбирать? Реально настолько дебил? То есть, не совмещает горы и горизонт, а тупо "трах-тибидох", получает сам не понимает что?

3-62> Будет наблюдаться изменение ОТНОСИТЕЛЬНОГО положения предметов (разноудаленных) пропорционально их расстоянию от камеры "в глубину".
3-62> И "точка нулевого параллакса" - будет, скажем так "на горизонте". Независимо от "базы камеры".

Да, Вы совершенно правы.

Тут возникла путанница между точкой нулевого параллакса и "нулевой точкой" на кадрах - точке пересечения двух кадров в точке ОТЛИЧНОЙ от точки 0-параллакса.

Если кадры пересекаются в такой точке (на гифе), то мы это видим как "вращение".
Это вращение верный знак, что кадры надо РАЗДВИНУТЬ, чтобы они пересеклись в истинной точке нулевого параллакса ("на горизонте")

Hal> Ну так теперь ты понял что софт выбрал не те точки? Или будешь дальше упираться как баран в своей тупости?
Phazeus> Оно что, спрашивает у софта, какие точки выбирать? Реально настолько дебил? То есть, не совмещает горы и горизонт, а тупо "трах-тибидох", получает сам не понимает что?

Забавно наблюдать, как беседуют ТУПОЙ и ЕЩЁ ТУПЕЕ о вещах в которых ничего не понимают, ну просто песня.


Ос> На каком основании ты выводишь размер макета 1:3?


Постулировал, что от камеры до ровера в этот момент 10 м

Угол охвата камеры 54.9°. Угловой размер по ширине колеи ровера 3.46°

Отсюда вытекает, что он уже оригинала (1.82 м), в 3 раза
Значит для съемок нам нужно иметь 102 кадра в секунду
√(6n)*24=√(6*3)*24=102.

В рамках данного предположения горы насыпаны на расстоянии около 20 метров от камеры

Постулат выдвинут из соображений, чтобы всё вместилось в вакуумной камере (ее диаметр 30 м)

Phazeus> Оно что, спрашивает у софта, какие точки выбирать? Реально настолько дебил? То есть, не совмещает горы и горизонт, а тупо "трах-тибидох", получает сам не понимает что?

Это ты не понимаешь, что и где вообще происходит. У тебя в статусе написано "опытный", надо было написать "опытный троглодит"))

aФон>>> Ваш гиф, как раз и подтверждает мои слова, просто Вы это не осознаете.
Tangaroa>> Мой гиф опровергает твои слова, просто ты это ещё не осознал.
Tangaroa>> Смотри ещё раз:
Tangaroa>> http://j-p-g.net/if/2019/02/19/0268857001550555739.gif
aФон> Дурачок, сравни эти две гифки
начнём с того, что дурачок это твой папа

aФон> Вращение вокруг точки на кадре УКАЗЫВАЕТ, что есть БОЛЕЕ УДАЛЕННЫЕ ОБЪЕКТЫ.
...и эти удалённые объекты - это горы. Не подножье гор, а более дальний план.

Смотри сюда:


Параллакса - нет

aФон> Постулировал, что от камеры до ровера в этот момент 10 м
Постулирую: афон - идиот.

Tangaroa> Смотри сюда:
Tangaroa> http://www.balancer.ru/sites/com/dr/.../Grand_Prix_-_2.png.gif


Простого поворота и сдвига недостаточно, чтобы привести эти снимки к одной проекции:

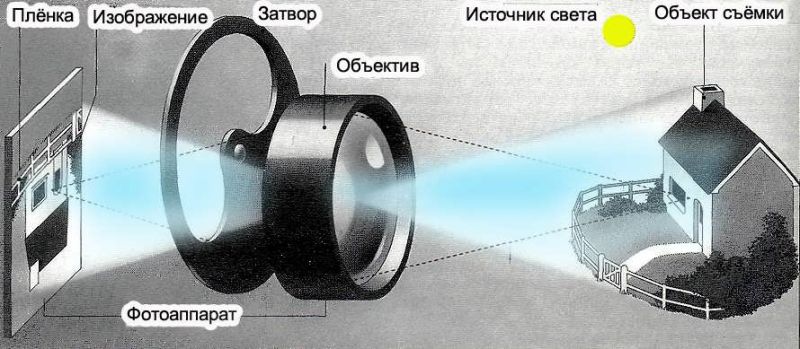
На фотографиях, картинах, экране изображения кажутся нам естественными и правильными. Эти изображения называют перспективными. Свойства их таковы, что более удаленные предметы изображаются в меньших масштабах, параллельные прямые в общем случае непараллельны. В итоге геометрия изображения оказывается достаточно сложной, и по готовому изображению сложно определить размер тех или иных частей объекта.

Обычная перспективная проекция — это центральная проекция на плоскость прямыми лучами, проходящими через точку — центр проецирования. Один из проецирующих лучей перпендикулярен к плоскости проецирования и называется главным. Точка пересечения этого луча и плоскости проекции — главная точка картины.

Существует три системы координат. Обычно программист работает и держит данные о геометрических объектах в мировых координатах. Для повышения реалистичности при подготовке к выводу изображения на экран данные об объектах из мировых координат переводят в видовые координаты. И только в момент вывода изображения непосредственно на экран дисплея переходят к экранным координатам, которые представляют собой номера пикселов экрана.

Первые две системы могут использоваться в многомерных системах координат, но последняя только в двухмерной. Операции являются необратимыми, то есть из двухмерной картинки-проекции невозможно восстановить трехмерное изображение.
Матрица общего перспективного преобразования



В этой матрице элементы a, d, е отвечают за масштабирование, m, n, L — за смещение, p, q, r — за проецирование, s — за комплексное масштабирование, х — за вращение.

Часть I / Лекция 04. Перспективное проецирование

На прошлой лекции мы говорили о наиболее важных проекциях, ипользующихся в аффинной геометрии. Перейдем теперь к рассмотрению перспективной геометрии и нескольких новых видов проецирования. На фотографиях, картинах, экране изображения кажутся нам естественными и правильными. Эти изображения называют перспективными. Свойства их таковы, что более удаленные предметы изображаются в меньших масштабах, параллельные прямые в общем случае непараллельны. В итоге геометрия изображения оказывается достаточно сложной, и по готовому изображению сложно определить размер тех или иных частей объекта. //  Дальше — stratum.ac.ru

 

 

aФон> Постулат выдвинут из соображений, чтобы всё вместилось в вакуумной камере (ее диаметр 30 м)


Следовательно, кроме твоего желания притянуть за уши, других оснований у тебя нет.

Давай вспомним, что наши лжеспецы постулируют скорость съемки космонавтов в 2,5 раза выше реальной. Соответственно, нам надо на макет взять коэффициент уменьшения и получить скорость съемки в 5-6 раз выше реальной. Ты видел в моем ролике про риг Ховарда как это выглядит. Выглядит это абсолютно непохоже на реалтность,следовательно, ровер не может быть размером 1:3. Напомню,ты сам отказался от этого масштаба в этой теме.

Господа, а давайте завязывать с этими мерзкими метаниями фекалий друг в друга? Уже противно, на родителей перешли.

Tangaroa>> Смотри сюда:
Tangaroa>> http://www.balancer.ru/sites/com/dr/.../Grand_Prix_-_2.png.gif
aФон> Простого поворота и сдвига недостаточно, чтобы привести эти снимки к одной проекции:

Простого поворота и сдвига достаточно, чтобы убедиться в том, что там нет никаких вращающихся гор.

aФон> Но когда идет преобразование к общей проекции и проверка удаленности контрольных точек, то этого произвола уже нет.
aФон> Пустозвон, ну скачай Hugin, он в свободном доступе, можешь о нем и почитать тут
aФон> Сшиватель панорам Hugin и связанные с ним программы
aФон> И попробуй натянуть сову на глобус.
aФон> Да нельзя ничего там уговорить, ну попробй уговори, если оно не уговаривается.
aФон> Если только точность загрубить, возможно что-то и натянгете, но это если будете лохам впаривать результат, как Красильников тут по началу пытался врать, но быстро был изобличён.

Во-первых, если "оно не уговаривается", так это просто потому, что эта программа вообще не предназначена для сшивания стереопар — она заточена под панорамы, в её интерфейсе и хелпе никаких упоминаний про стереопары или анаглифы я не обнаружил (версия 2018.0.0.5abfb4de7961). В куче EXE-шников, идущих в комплекте, обнаруживается какое-то приложение align_image_stack, работающее из командной строки и не особо документированное, которое сооружает стереопары, но, насколько я понял из его куцей документации, точки соответствия находит автоматически. Описаний использующихся в нём алгоритмов я не нашёл. Таким образом, нет никаких доказательств, что этот софт вообще умеет корректно восстанавливать расположение объектов по глубине из пары кадров, а значит, все основанные на нём рассуждения о "насыпанных горах" гроша выеденного не стоят.

Во-вторых, как мы уже убедились на ряде примеров, полностью реалистичная стереопара может быть построена (причём без всяких там Hugin'ов) с неподвижной точкой на любой глубине. Поэтому скачки гор на заднем плане означают не то, что эти горы находятся в 20 метрах от объектива, а только то, что программе по какой-то своей внутренней причине захотелось установить неподвижную точку на среднем плане, а не на бесконечности. В целом это напоминает попытки численно решить уравнение с множеством корней, например sin x=0, с помощью не слишком хитроумной программы. Если вы выберете (или программа подскажет) начальное приближение где-нибудь недалеко от нуля, то итерации быстро сойдутся к х=0. Но решений на самом деле бесконечно много, и было бы глупо заявлять: "Никаких 2*пи и 7*пи не может быть, потому что моя программа насчитала ноль!"

Tangaroa> Смотри сюда:

А ты не видишь что у тебя точки на горе гуляют пикселей на 15 влево-вправо? Из такого совмещения невозможно делать совершенно никаких выводов.

Tangaroa>> Смотри сюда:
Лунит> А ты не видишь что у тебя точки на горе гуляют пикселей на 15 влево-вправо? Из такого совмещения невозможно делать совершенно никаких выводов.

Гуляют, да. Потому что дисторсия.
Но ничего не вращается

kfmn> Во-первых, если "оно не уговаривается", так это просто потому, что эта программа вообще не предназначена для сшивания стереопар — она заточена под панорамы, в её интерфейсе и хелпе никаких упоминаний про стереопары или анаглифы я не обнаружил (версия 2018.0.0.5abfb4de7961).

Нам и не нужно получать стереопары - это ложный посыл.
Нам нужно два снимка привести к одинаковой проекции, это и делает Hugin

kfmn>В куче EXE-шников, идущих в комплекте, обнаруживается какое-то приложение align_image_stack, работающее из командной строки и не особо документированное, которое сооружает стереопары,

Кто тебя пустил по этому ложному следу, зачем нам сдались эти стереопары?

kfmn> Таким образом, нет никаких доказательств, что этот софт вообще умеет корректно восстанавливать расположение объектов по глубине из пары кадров, а значит, все основанные на нём рассуждения о "насыпанных горах" гроша выеденного не стоят.

Софт умеет свести два кадра к одинаковой проекции, выполняет над ними соответствующие преобразования.

kfmn> Во-вторых, как мы уже убедились на ряде примеров, полностью реалистичная стереопара может быть построена (причём без всяких там Hugin'ов) с неподвижной точкой на любой глубине. Поэтому скачки гор на заднем плане означают не то, что эти горы находятся в 20 метрах от объектива, а только то, что программе по какой-то своей внутренней причине захотелось установить неподвижную точку на среднем плане, а не на бесконечности.

Да, вращение вокруг точки, означает, что эта точка не есть точка нулевого параллакса и она выбирается не программой, а пользователем

kfmn> В целом это напоминает попытки численно решить уравнение с множеством корней, например sin x=0, с помощью не слишком хитроумной программы. Если вы выберете (или программа подскажет) начальное приближение где-нибудь недалеко от нуля, то итерации быстро сойдутся к х=0. Но решений на самом деле бесконечно много,

В нашем случае, если мы прижались к вершинам гор с выбором нулевых точек, а вращение не исчезло, то это верный признак, что вершины гор очень далеки от горизонта.

Tangaroa> Простого поворота и сдвига достаточно, чтобы убедиться в том, что там нет никаких вращающихся гор.

Увы, не достаточно.
Кадры получены при совершенно разных наклонах камеры к горизонту, а ты считаешь, что плоскость пленки все время имеет ОДИНАКОВЫЙ УГОЛ С ГОРИЗОНТОМ

aФон> В нашем случае, если мы прижались к вершинам гор с выбором нулевых точек, а вращение не исчезло, то это верный признак, что вершины гор очень далеки от горизонта.
При этом горизонт всего в двух километрах, не забывай.

aФон> Увы, не достаточно.
aФон> Кадры получены при совершенно разных наклонах камеры к горизонту, а ты считаешь, что плоскость пленки все время имеет ОДИНАКОВЫЙ УГОЛ С ГОРИЗОНТОМ

Для того, чтобы понять, что там нет вращающихся гор, этого вполне достаточно.

Tangaroa> Параллакса - нет

Хочешь сказать, что аферисты пользовались специальной насадкой для поворота камеры относительно нодальной точки?

Если нет параллакса, то значит камеру вращал не человек, а робот относительно нодальной точки и никак иначе.

Я тебе советую присмотреться к этим кадрам, они на твою версию, что параллакса нет, работают

Tangaroa>> Параллакса - нет
aФон> Хочешь сказать, что аферисты пользовались специальной насадкой для поворота камеры относительно нодальной точки?
Нет. Я хочу сказать, что астронавты не пользовались никакими хитроумными киноприспособами и не совершали каких-то "студийных приёмов" кроме того, что они прилетели на Луну и сняли несколько роликов 16-мм кинокамерой, адаптированной под такие необычные условия.

aФон> Если нет параллакса, то значит камеру вращал не человек, а робот относительно нодальной точки и никак иначе.
Горы не "вращаются", эти искажения картинки - артефакты, возникающие при её обработке.

aФон> Я тебе советую присмотреться к
Я тебе советую обратиться к врачам. Они помогут тебе достойно прожить остаток жизни, но, к сожалению, никто уже не поможет справиться с сожалением о бездарно просранных годах.

Tangaroa> Горы не "вращаются", эти искажения картинки - артефакты, возникающие при её обработке.

А почему такие "артефакты" возникают только на кадрах от аферистов, а все другие фотографии ничего подобного не выдают?

Ос> Господа, а давайте завязывать с этими мерзкими метаниями фекалий друг в друга? Уже противно, на родителей перешли.

это возможно при общении с людьми. Увы, с данными персонажами общение по-иному просто невозможно. Они такие по жизни.
А я считаю, что попытка общаться с ними по-человечески - есть неуважение к людям.

kfmn> Во-первых, если "оно не уговаривается", так это просто потому, что эта программа вообще не предназначена для сшивания стереопар — она заточена под панорамы

Программа - это инструмент. Как молоток. Она не обязательна. Всё это можно сделать в обычном Гимпе руками. Вопрос в том, что если рукожопый дебил берётся делать что-то, о чём не имеет ни малейшего понятия, не обладает даже бытовым опытом, то получается эпическая несуразная чертовщина.
Эти дауны не понимают даже, что делают. И что самое бесящее - не способны понять в принципе и не имеют к тому ни малейшего желания.

kfmn> а только то, что программе по какой-то своей внутренней причине захотелось установить неподвижную точку на среднем плане, а не на бесконечности

Дело даже не в этом. В данном случае горы будут всё равно "крутиться", так как точка одна, а он вместо совмещения гор сделал "телепание" вокруг "нулевой точки", как он выразился. При таком идиотском подходе любая фотка будет давать именно такой эффект, что прекрасно демонстрирует пара с балкона.

Tangaroa>> Горы не "вращаются", эти искажения картинки - артефакты, возникающие при её обработке.
aФон> А почему такие "артефакты" возникают только на кадрах от аферистов, а все другие фотографии ничего подобного не выдают?

Потому что ты криворукий болван, страстно желающий добиться появления этих артефактов. Ведь ты не ищешь ответ — он тебе известен заранее, поэтому ты подгоняешь под него все свои измышления.

aФон> Нам и не нужно получать стереопары - это ложный посыл.
Ну конечно не нужно! Зачем тебе видеть что никакого параллакса на задних горах нет, если тебе нужен символ веры - растягивающиеся горы, которые выглядят как поворот?

aФон> Кто тебя пустил по этому ложному следу, зачем нам сдались эти стереопары?
Чтобы не быть бздунишкой, типа тебя.
Чтобы можно было четко увидеть, что качание и растягивание гифки не означает наличие параллакса.
Любой след аФон объявит ложным, если это рушит его влажную религию.

Hal> Любой след аФон объявит ложным, если это рушит его влажную религию.

Афон за последний месяц умудрился опровергнуть свои схемы съемки, отказаться от десяти лет своей "работы" и выставить петухами своих кумиров, и начал цитировать учебники и источники. Будем к нему снисходительны, он потерял почву под ногами.

Tangaroa> Гуляют, да. Потому что дисторсия.
Tangaroa> Но ничего не вращается

Не гони, дисторсия не помешала совмещению вот здесь:

У тебя хотя бы некоторые точки должны совпадать, ближе к центру, а в реальности у тебя гуляет вообще всё. Значит что-то не так совместил.

Лунит> Не гони, дисторсия не помешала совмещению вот здесь:
Лунит> https://www.balancer.ru/sites/com/.../stereoparallax/appolo_15_S13.gif

Сравнил жо... сорри, калий с кальцием.
Наверное, все-таки есть разница между 70-мм слайдом и 16 мм кинопленкой и соответствующей оптикой. Да и насколько был пережат исходный ролик, когда его в mpeg пересобачивали.